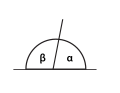Kulma
Kulma (josta käytetään erotukseksi avaruuskulmasta myös nimitystä tasokulma) on geometriassa kahden säteen väliin jäävän tason osa. Kulmalla tarkoitetaan myös osan suuruutta, joka ilmoitetaan lukuarvona. Kulmia syntyy kolmioiden kärkiin, suorien ja janojen väliin ja moniin geometrisiin kuvioihin. Janat, suorat ja kulmat muodostavat alkeisgeometrian perustan. Kulmia käytetään asentojen mittaamisessa tieteessä ja tekniikassa.[1][2][3]
-
Kulma α kulmamerkintänä kahden säteen välissä.
-
Kulma voidaan ajatella olevan säteiden välissä oleva kiilamainen alue (harmaa).
-
Suorien välisiä kulmia.
-
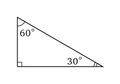
Kolmiossa kahden kulman suuruus on ilmoitettu asteina.
Kulman määritelmä ja sen osat[muokkaa | muokkaa wikitekstiä]
Kahden samasta pisteestä alkavan puolisuoran (eli säteen) rajoittamaa tason osaa kutsutaan siis kulmaksi. Itse asiassa puolisuorat rajoittavat tasosta aina kaksi kulmaa, jotka ovat toistensa eksplementtikulmia. Se, kumpaa kulmaa tarkoitetaan, riippuu tilanteesta tai merkintätavasta. Tämä voidaan ilmaista sanomalla, minne kulma aukeaa ja merkitä se kuvioon kärjen lähelle piirretyllä kaarella. Aukeamissuunnassa kaikki puolisuorien välissä olevat pisteet ovat kulman pisteitä.[1][2]
Kulman muodostavia suoria, puolisuoria tai janoja on tapana kutsua kulman kyljiksi. Jotta kulma voidaan nimetä, tulee vähintään kulman kärjen pisteen nimi tuntea. Silloin voidaan nimetä kulma yhdellä kirjaimella ja esimerkiksi kulma B voidaan merkitä joko tai . Samasta kärjen pisteestä voi aueta eri suuntiin useita kulmia, jolloin pelkästään kärjen pisteeseen viittaaminen ei yksilöi kulmaa. Jos kummaltakin kyljeltä tunnetaan yksi piste, joidaan pisteiden nimiä käyttää kulman nimeämiseen. Esimerkiksi kulma B voi olla myös kulma ABC eli tai , jolloin säde BA on kulman oikea kylki ja säde BC sen vasen kylki. Merkinnän keskimmäinen kirjain on aina kulman kärjen nimi. Usein merkitään kulmaa kreikkalaisella kirjaimella, kun tarkoitetaan kulman nimeä tai kulman suuruutta (muuttuja).[1][2]
-
Eksplementtikulmat rajaavat tasoon kaksi osaa.
-
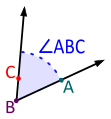
Oikea kylki on säde BA ja vasen kylki säde BC. Kulman lukeminen aloitetaan oikeasta kyljestä.
-
Merkitty kulma voidaan merkitä kulma B tai kolmikirjaimisena kulma ABC.
-
Kulman kolmikirjaiminen merkintätapa ja kiertosuunta.
Toisaalta kulma voidaan ajatella syntyneen siten, että oikea kylki pyyhkäisee vastapäivään ja pysähtyy vasemman kyljen kohdalle. Silloin käytetään kulman ABC kyljistä nimityksiä alkukylki BA ja loppukylki BC. Jos siitä on tarkastelun kannalta hyötyä, voidaan kulmaa pitää suunnattuna kulmana. Suunnatun kulman positiivinen kiertosuunta on useimmiten vastapäiväinen kiertosuunta ja negatiivisen on myötäpäiväinen kiertosuunta.[1][4]
Kulman suure ja yksiköt[muokkaa | muokkaa wikitekstiä]
Erotukseksi kulman geometrisesta oliosta, joka koostuu tason pisteistä, määritellään kulman suure. Kulman suure tarkoittaa kulman suuruutta eli "kuinka paljon kulma aukeaa". Ihmiskunnan historiassa kulman suuruutta on ilmaistu hyvin monella tavalla. Alkukantaisimmat mittayksiköt perustuivat oikokulman murto-osiin tai suoran kulman murto-osiin.
Kun kulman mittaamiseen kehitettiin välineitä, alettiin käyttämään hienojakoisia asteikkoja. Todennäköisesti babylonialaisilta on peräisin tapa jakaa täysi kulma 360 osaan, jota merkitään 360° (astetta).[5] Sen etu piilee luvun 360 jaollisuudessa, mutta muitakin asteikkoja käytetään. Ranskalaista alkuperää on tapa jakaa täysi kulma 400 osaan, jota merkitään 400 gon (goonia). Muut asteikot sivuttaen voidaan esitellä myös hyödyllisin asteikko, jossa täysi kulma ilmaistaan 1-säteisen ympyrän kehän pituudella. Täysi kulma on silloin (radiaania).[4][6][7][3]
Asteissa on käytössä kaksi tapaa esittää asteen murto-osia. Vanhempi tapa jakaa asteet 60-osiin eli kulmaminuutteihin (1° = 60') ja minuutit 60−osiin eli kulmasekunteihin (1' = 60"). Nykyään asteet jaetaan myös desimaaliosiin. Silloin on esimerkiksi 20°10'30" = 20,175°.[2]
Kolmiulotteisen avaruuskulman yksikkö puolestaan on steradiaani.[3]
Kulmien luokittelu[muokkaa | muokkaa wikitekstiä]
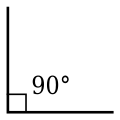
Teknisesti tärkeitä kulmia ovat suora kulma (90°) ja oikokulma (180°). Niiden avulla jaetaan kulmat erilaisiin luokkiin, jossa täysi kulma (360°) toimii jaottelun perustana. Oikokulma jakaa sen kahteen pääluokkaan: kovera kulma (0°−180°) ja kupera kulma (180°−360°). Kovera kulma voidaan jakaa suoran kulman avulla kahteen alaluokkaan: terävä kulma (0°−90°) ja tylppä kulma (90°−180°). Suora kulma ja oikokulma eivät kuulu raja-kulmina mihinkään jakamaansa luokkaan, mutta nollakulma ja täysi kulma jakaa mielipiteitä. Joissakin lähteissä nekin ovat raja-kulmia, mutta toisissa lähteissä nollakulma kuuluu teräviin kulmiin ja täysi kulma kuperiin kulmiin.[2][3]
-
Terävä kulma on pienempi kulma kuin suora kulma.
-
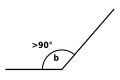
Tylppä kulma on suurempi kuin suora kulma, mutta pienempi kuin oikokulma.
-
Kupera kulma on suurempi kuin oikokulma, mutta pienempi kuin täysi kulma.
Kulmat reaalilukuina[muokkaa | muokkaa wikitekstiä]
Nykyaikaisessa kulman mittaamisessa tulee kulman arvon voida olla kuinka suuri tahansa ja toisinaan negatiivinen. Kulma voidaan ajatella syntyvän alkukyljestä, jonka aloitusasentoa merkitään kulman arvolla 0. Kun kylkeä kierretään vastapäivään, vastaa se kulman loppukylkeä. Loppu- ja alkukylkien välistä kulmaa kasvattamalla saadaan loppukylki lopulta aloittamaan uuden kierroksen ja kulman asteluvuksi tulee täyttä kulmaa suurempi kulma eli yli 360°. Rajoittamatta mitenkään kierroksien lukumäärää, voi kulman suuruus kasvaa kuinka suureksi tahansa.[4]
Hyväksymällä loppukyljelle myös myötäpäiväinen kiertosuunta ja erottamalla se vastapäivään kiertävästä kulmasta määrittämällä sen suunta negatiiviseksi, voidaan kiertämisen suunnista ja suuruuksista pitää kirjaa reaalilukujen aritmetiikalla.[4]
-
Positiivisen kulman suunta.
-
Kulma, jonka suuruus on 34° yli kierroksen, on 360° + 34° = 394°.
-
Positiivinen ja negatiivinen kulma radiaaneissa.
Kulmien relaatiot[muokkaa | muokkaa wikitekstiä]
Kulmien suuruuksia voidaan arvioida siirtämällä kulmat päällekkäin niin, että vähintään kärki ja oikeat kyljet yhtyvät toisiinsa. Tällöin kaksi kulmaa aukeavat yhtä paljon, jos myös niiden vasemmat kyljet yhtyvät toisiinsa. Yleensä tämä riittää, kun halutaan todeta kulmien yhtäsuuruus, mikä merkitään . Mikäli kulmat ovat suunnattuja, tutkitaan yhtäsuuruus asettamalla kärjet ja alkukylki päällekkäin. Mikäli loppukyljet yhtyvät, ovat kulmat yhtäsuuret. Mikäli eivät, voivat kulmat olla toistensa vastakulmat, mikäli kulmat aukeavat yhtä paljon. Tämä tilanne merkitään .[1]
Mikäli päällekkäin asetetut kulmat aukeavat eri tavalla, ovat kulmat erisuuruiset ja se merkitään . Kulmille voidaan määritellä myös järjestysrelaatio. Se kulma on suurempi, joka aukeaa enemmän. Suunnatuissa kulmissa se kulma on suurempi, joka aukeaa enemmän vastapäivään tai aukeaa vähemmän myötäpäivään kuin toinen. Tämä tilanne merkitään merkitään .
Kulmien laskutoimitukset[muokkaa | muokkaa wikitekstiä]
Kaksi kulmaa ovat vierekkäiset, jos niillä on yhteinen kylki ja kärjet yhtyvät toisiinsa. Kulmien yhteenlasku voidaan määritellä vierekkäisten kulmien yhdistelmäksi. Vähennyslasku voidaan ratkaista myös piirtämällä. Kulmat piirretään päällekkäin siten, että kärjet ja vasemmat kyljet yhtyvät. Oikean puoleisten kylkien välinen kulma on erotuksen suuruus.
Myös suunnatuilla kulmilla voidaan laskea yhteen- ja vähennyslaskua. Yhteenlaskun laskutoimitus voidaan suorittaa piirtämällä ensimmäinen kulma paperille. Summan toinen kulma piirretään niin, että ensimmäisen kulman loppukylkelle sijoitetaan toisen kulman alkukylki ja toisen kulman loppukylki piirretään suunnatun kulman määräämään suuntaan. Vähennyslaskussa toisen kulman alkukylki piirretään ensimmäisen kulman loppukylkeen, mutta toisen kyljen loppukylki piirretään vastakkaiseen kiertosuuntaan kuin sen oma kiertosuunta on. Kulmien yhteen- ja vähennyslaskut suoritetaan kulmien lukuarvoilla ja huomioimalla kulmien suunnat lukuarvojen etumerkeillä, saadaan summat reaalilukujen laskusääntöjä noudattamalla.
-
Vierekkäisten kulmien yhdistelmä on kulmien geometrinen summa.
-
Yhteen ja vähennyslasku voidaan määritellä suunnattujen kulmien avulla.
-
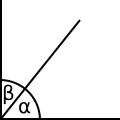
Komplementtikulmat:
α + β = 90°. -
Suplementtikulmat:
α + β = 180°. -
Eksplementtikulmat:
α + β = 360°.
Yhteenlaskun erikoistapaukset[muokkaa | muokkaa wikitekstiä]
Tasogeometriassa on ollut erityisasemassa sellaiset kahden kulman summat, jotka ovat yhteensä suora kulma, oikokulma tai täysi kulma. Jos kahden kulman summa on 90° niin kulmat ovat toistensa komplementtikulmia. Vastaavasti, jos kulmien summa on 180°, ovat kulmat toistensa suplementtikulmia, ja jos kulmien summa on 360°, ovat ne toistensa eksplementtikulmia.
Kulman mittaaminen[muokkaa | muokkaa wikitekstiä]
Tieteellinen mittaus[muokkaa | muokkaa wikitekstiä]
Nykyaikaisessa SI-järjestelmässä kulman mittaaminen suoritetaan käyttäen pituusmittoja ja tulos ilmaistaan niin sanoittuina "radiaaneina". Tasokulma määritellään SI-järjestelmässä johdannaissuureena, jossa esimerkiksi täyden kulman arvo saadaan ympyrän kehän pituuden ja ympyrän säteen suhteesta (eli ). Kulman arvot ovat mittayksiköttömiä.[8]
Tasokulman mittaamiseen voidaan käyttää myös muita, SI-järjestelmään kuulumattomia, tapoja. Esimerkiksi asteet määritellään kansainvälisessä SI-järjestelmän sopimuksessa . Tämän murto-osina käytetään kulmaminuutteja ja kulmasekunteja. Myös gooneja käytetään erityistapauksissa.[8][9]
Arkipäivän mittaus[muokkaa | muokkaa wikitekstiä]
Tasokulman suurelle voidaan määrittää likiarvo mitata se esimerkiksi kulmamitalla tai sille voidaan määrittää tarkka arvo laskemalla se suorakulmaisen kolmion sivujen suhteiden perusteella (trigonometria).[9]
Kulman puolittaminen[muokkaa | muokkaa wikitekstiä]

Kulman puolittajaksi kutsutaan puolisuoraa, joka jakaa kulman kahteen yhtä suureen osaan. Se voidaan konstruoida Eukleideen Alkeiden opettamalla tavalla käyttäen vain harppia ja viivainta.[10]
Kulma voidaan kulmaviivaimen avulla puolittaa piirtämällä sellainen kulman kautta kulkeva puolisuora, joka jakaa kulman edelleen kahteen pienempään kulmaan, jotka ovat yhtä suuria. Esim. 48 asteen kulma puolitetaan piirtämällä kulman kautta kulkeva sellainen puolisuora, joka jakaa kulman edelleen kahteen 24 asteen pienempään kulmaan.[10]
Kulma voidaan puolittaa myös geometrisesti pelkkää harppia apuna käyttäen. Kulman puolittaminen geometrisesti[10]:
1. Piirretään kulman O kärkipiste keskipisteenä harpin avulla kaari. Merkitään kaaren ja kulman kylkien leikkauspisteitä vaikkapa kirjaimilla A ja B.
2. Piirretään pisteet A ja B keskipisteinä uudelleen kaksi keskenään samansäteistä ympyrän kaarta niin, että ne leikkaavat toisiaan kulman O kentässä.
3. Piirretään puolisuora, joka kulkee pisteestä O pisteiden B ja A kaarien leikkauspisteeseen. Merkitään leikkauspistettä vaikkapa kirjaimella C. Kyseessä on kulman O puolittaja.
Katso myös[muokkaa | muokkaa wikitekstiä]
Lähteet[muokkaa | muokkaa wikitekstiä]
- ↑ a b c d e Väisälä, Kalle: Geometria, s. 8–10. Porvoo: Wsoy, 1959. Teoksen verkkoversio (pdf).
- ↑ a b c d e Kontkanen, Pekka & al.: Pyramidi 3, s. 15–18. (lukion pitkän matematiikan oppikirja). Helsinki: Tammi, 2005. ISBN 978-951-26-5059-0.
- ↑ a b c d Weisstein, Eric W.: Angle (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)
- ↑ a b c d Kontkanen, Pekka & al.: Pyramidi 9, s. 10–15. (lukion pitkän matematiikan oppikirja). Helsinki: Tammi, 2007. ISBN 978-951-26-5403-1.
- ↑ Weisstein, Eric W.: Degree (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)
- ↑ Hogben, Lancelot: Matematiikkaa kaikille, s. 41–48. Suomentanut Risto Niini. Porvoo: Werner Söderström OY, 1945.
- ↑ Boyer, Carl B. & Merzbach, Uta C.: Tieteiden kuningatar – Matematiikan historia, osa I, s. 51–57. Suomentanut Kimmo Pietiläinen. Helsinki: Art House, 1994. ISBN 951-884-150-0.
- ↑ a b The International System of Units (SI) Bureau International des Poids et Mesures.
- ↑ a b Suomen Standardoimisliitto: SI-opas (myös painettuna, ISBN 952-5420-93-0) (PDF) (Sivu 3.) SFS-oppaat. 04.11.2002. Suomen Standardoimisliitto. Arkistoitu 31.8.2012. Viitattu 18.2.2013.
- ↑ a b c Tammi: Matematiikan teoriakirja Kolmio 2009