Suora kulma

Suora kulma on geometriassa sellainen kulma, joka on yhtä suuri kuin sen kumpi tahansa vieruskulma.[1] Suoran kulman suuruus on neljäsosa täydestä kulmasta tai puolet oikokulmasta eli 90°. Se on tärkein arjessa käytettävä kulma.[2] Janojen kohtisuoruus on synonyymi sille, että janojen väliset kulmat ovat suoria. Suomenkielinen ilmaus suora kulma viitannee "pystyssä olemiseen" eli "suorassa seisomiseen".[3]
Suora kulma eri kulma-asteikoilla[muokkaa | muokkaa wikitekstiä]
Suora kulma on
- täydestä kulmasta ja oikokulmasta.[4]
- 90° (astetta), kun täysi kulma on 360°.[2]
- 100 gon (goonia), kun täysi kulma on 400 gon.
- radiaania, kun täysi kulma on .[2]
Esimerkkejä[muokkaa | muokkaa wikitekstiä]
- Janan keskinormaalilla on leikkauspisteessään neljä suoraa kulmaa.
- Suorakulmaisessa koordinaatistossa akseleiden välinen kulma on suora.
- Suorakulmaisessa kolmiossa yksi sen kulmista on suora. Sellaisia ovat muun muassa kolmiot, joiden sivut ovat 3-4-5 tai 5-12-13 yksikköä pitkät. Suoran kulman viereisiä sivuja kutsutaan kateeteiksi.
- Neliön ja suorakulmion kaikki kulmat ovat suoria kulmia.
- Neljäkkään ja leijan lävistäjät leikkaavat toisensa suorassa kulmassa.
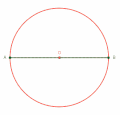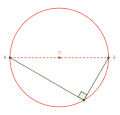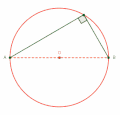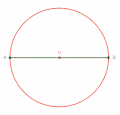
- Puoliympyrän kehäpisteen ja halkaisijan päätepisteiden väliset janat ovat suorassa kulmassa.
- Kahden suoran välinen kulma on suora, jos suorien yhtälöiden kulmakertoimien tulo on -1.
- Kaksi kulmaa ovat toistensa komplementtikulmat, jos niiden summa on suora kulma.
-
Suorakulmainen kolmio, jonka sivut ovat 3-4-5.
-
Neliön puolikas sisältää suoran kulman ja on helppo piirtää.
Mittaminen ja piirtäminen[muokkaa | muokkaa wikitekstiä]
Geometrinen konstruktio[muokkaa | muokkaa wikitekstiä]
Suoran kulman merkitseminen tasolle käyttämällä vain viivainta ja harppia oli aiemmin tärkeä käytännön taito. Suoran kulman konstruoimiseksi tunnetaan runsaasti erilaisia menetelmiä. Seuraavassa on muutama menetelmä.
- Janalle voi piirtää keskinormaalin merkitsemällä harpilla kaksi normaalin pistettä ja piirtämällä niiden kautta kohtisuora viiva. Tämä vastaa oikokulman puolittamista.[5]
- Janalle voidaan harpilla piirtää tasasivuinen kolmio, jonka 60° kulma puolitetaan. Syntyy kaksi suorakulmaista kolmiota. Toinen suorakulmainen kolmio voidaan irrottaa ja siirtää käännettynä toisen puolikkaan viereen, jolloin syntyy suorakulmio.
- Kun ympyrän halkaisijan päätepisteistä piirtää janat samaan kehäpisteeseen, syntyy siihen suora kulma (Thaleen lause).[6]
-
Animaatio harpin käytöstä normaalia piirrettäessä.
-
Pisteen P kautta voidaan aina piirtää suoralle normaali. Punaisella kaarella merkitään suoralta kaksi pistettä. Näistä piirretään P:n kautta kaksi vihreää kaarta, jotka leikkaavat myös Q:ssa. Pisteet P ja Q yhdistetään normaaliksi.
-
Tasasivuinen kolmio puolitetaan. Puolitusjana on suorassa kulmassa.
-
Thaleen lause puoliympyrän kehäkulmasta, joka on suora kulma.
Mittavälineitä[muokkaa | muokkaa wikitekstiä]
Käsityön ammattilaisilla on käytössään monia työkaluja suoran kulman määrittämiseksi. Tunnetuin on suorakulma, jolla voidaan merkitä tai tarkistaa kulman suoruus. Myös normaalin merkitsemiseen on käytössä sekä asteikolla varustettuja mittalevyjä että optisia välineitä. Uusimmat laitteet osoittavat kohtisuoruuden laser säteellä.
-
Egyptiläinen suora kulma.
-
Niin sanotussa "kombikolmiossa" on normaali eli 90° merkitty selvästi.
-
Prisman peilikuvien avulla voidaan sijoittautua kohteessa suoraan kulmaan.
-
Suunnittelijan suora kulma.
Historia[muokkaa | muokkaa wikitekstiä]

Ei ole tietoa siitä, koska suora kulma on opittu mittaamaan, sillä jo ensimmäisillä kirjoitettua tietoa jälkeensä jättäneillä kansoilla tiedetään tämä taito jo olleen. Yksinkertaisin keino muodostaa suora kulma perustui painovoimaan: luotinarun ja vesivaa'an välinen kulma on suora. Toinen yleisesti tunnettu keino muodostaa suora kulma vakatasossa oli käyttää narua, johon oli solmittu tasavälein 13 solmua. Kun tämä naru pingotettiin kolmioksi, jonka sivuiksi asetettiin kolme, neljä ja viisi solmuväliä, saatiin suorakulmainen kolmio. Tämä sääntö tunnetaan yhtenä numerokolmikkona, joka toteuttaa Pythagoraan lauseen.[7]
Euklideen Alkeet[muokkaa | muokkaa wikitekstiä]
Laajalti tunnetussa oppikirjassaan Alkeet Euklides määrittelee kirjassa I määritelmässä 10 kohtisuorat suorat ja määritelmässä 4, että kaikki suorat kulmat ovat yhtä suuret. Määritelmissä 11 ja 12 nimeää hän terävät kulmat suoraa kulmaa pienemmiksi ja tylpät suuremmiksi.[8]
Katso myös[muokkaa | muokkaa wikitekstiä]
Muita kulman nimityksiä: nollakulma, terävä kulma, tylppä kulma, kovera kulma, oikokulma, kupera kulma ja täysi kulma.
Lähteet[muokkaa | muokkaa wikitekstiä]
- ↑ Lehtinen, Matti: Geometrian perusteita (pdf) (sivu 16) http://www.elisanet.fi/matti.t.lehtinen/. Viitattu 31.8.2016.
- ↑ a b c Weisstein, Eric W.: Right Angle (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)
- ↑ Häkkinen, Kaisa: Nykysuomen etymologinen sanakirja. Helsinki: WSOY, 2007. ISBN 978-951-27108-7.
- ↑ Weisstein, Eric W.: Full Angle (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)
- ↑ Hogben, Lancelot: Matematiikkaa kaikille, s. 126–128. Suomentanut Risto Niini. Porvoo: Werner Söderström OY, 1945.
- ↑ Weisstein, Eric W.: Thales' Theorem (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)
- ↑ Hogben, Lancelot: Matematiikkaa kaikille, s. 48–53. Suomentanut Risto Niini. Porvoo: Werner Söderström OY, 1945.
- ↑ Joyce, David E.: Kirjan I määritelmät, 1996