Neljäkäs

Neljäkäs on geometriassa nelikulmio, jonka kaikki neljä sivua ovat yhtä pitkät. Tämä ominaisuuden takia se kuuluu tasasivuisiin monikulmioihin. Toisaalta neljäkäs kuuluu myös suunnikkaisiin, sillä sen vastakkaiset sivut ovat aina yhdensuuntaiset. Neljäkkäästä käytetään myös nimiä rombi, vinoneliö[1] ja salmiakkikuvio.
Neljäkkään kulmien ei tarvitse olla suoria. Neljäkkään erikoistapausta, jossa kulmat ovat suorat, kutsutaan neliöksi. Joskus vinoneliöllä tarkoitetaan erityisesti sellaista neljäkästä, joka ei ole neliö.[2]
Erityispiirteitä[muokkaa | muokkaa wikitekstiä]
Yksinkertainen nelikulmio on neljäkäs jos ja vain jos [3][4]
- kaikki sivut ovat yhtä pitkät (määritelmä).
- lävistäjät leikkaavat toisensa kohtisuoraan ja puolittavat toisensa.
- lävistäjät puolittavat kaikki sisäkulmat.
Seuraavat lauseet ovat niin sanottuja riittävyysehtoja eli neljäkäs on suunnikas,
- jolla vähintään kaksi vierekkäistä sivua ovat yhtä pitkät.
- jonka lävistäjät leikkaavat toisensa kohtisuoraan.
- jolla vähintään yksi lävistäjä puolittaa sisäkulmat.
Ominaisuuksia[muokkaa | muokkaa wikitekstiä]

Neljäkäs on aina yksinkertainen ja konveksi monikulmio.
Kulmat[muokkaa | muokkaa wikitekstiä]
Koska neljäkäs on suunnikas, on sen vastakkaiset sisäkulmat aina yhtäsuuret. Vierekkäiset kulmat α ja β ovat yleensä eri suuruiset paitsi neliöllä, jolla ne ovat yhtä suuret. Neljäkkään sisäkulmien summa on 360° ja vierekkäiset kulmat ovat toistensa suplementtikulmat eli α + β = 180°. Lyhintä lävistäjää vastaan on aina pienin kulma.
Lävistäjät puolittavat neljäkkäitä monin eri tavoin ja ne puolittavat myös kaikki sisäkulmat. Jos kulmia merkitään ja , niin lävistäjien puolittamat kulmat ovat (p:n halkaisema) ja (q:n halkaisema). Nämä ovat vastaavasti toistensa komplementtikulmia eli γ + δ = 90°.
Lävistäjät[muokkaa | muokkaa wikitekstiä]

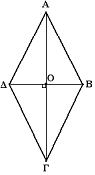
Yksinkertaisessa nelikulmiossa on aina lävistäjää (tässä ja ), jotka suunnikkaissa puolittavat toisensa ja neljäkkäässä vielä leikkaavat kohtisuorasti toisensa. Koska sivut ovat kaikki yhtä pitkät, riippuvat lävistäjien pituudet sisäkulmien suuruuksista
- ja
- .[5]
Pythagoraan lauseesta seuraa riippuvuus
- .[5]
Muita mittoja[muokkaa | muokkaa wikitekstiä]
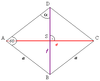
Oheisen kuvion muut merkityt janat voidaan laskea
Lävistäjät puolittavat vuorollaan neljäkkään pinta-alan. Kuten muidenkin suunnikkaiden, myös neljäkkään pinta-ala on sen kannan ja korkeuden tulo, toisin sanoen sivun pituuden ja sen kanssa yhdensuuntaisen sivun välisen etäisyyden tulo
- .[5]
Koska neljäkäs on tangentiaalinen nelikulmio, voidaan ala laskea myös
- ,[6]
missä on puolipiiri.
Ala on myös yhtä suuri kuin lävistäjien tulon puolikas eli
- .
Sisäympyrä[muokkaa | muokkaa wikitekstiä]
Neljäkkääseen voidaan aina piirtää ympyrä siten, että se sivuaa kaikkia neljäkkään sivuja sen sisäpuolelta. Tätä ympyrää voidaan kutsua sisäympyräksi. Neljäkäs on siten tangentiaalinen nelikulmio. Neljäkkään ympäri ei aina pysty piirtämään ympyrää siten, että sen kärjet olisivat ympyrän kehällä. Sellaisen voi piirtää vain neliölle, mutta ei muille neljäkkäille. Sisäympyrän säde voidaan laskea kahdella eri tavalla [7][8][6]
Sisäympyrän keskipiste O sijaitsee aina lävistäjien leikkauspisteessä. Sisäympyrän sivuamispisteet, jotka on merkitty oheiseen kuvioon kirjaimilla J, K, L ja M, osuvat kehälle kohtiin, jotka riippuvat neljäkkään muodosta. Neljäkkään sivut ovat kohtisuorassa sädettä vastaan. Sivujen etäisyydet keskipisteestä ovat siten aina (säde), jolloin kahden vastakkaisen sivun välimatka, joka on neljäkkään korkeus, on silloin .
Koska neljäkkään sivut ovat kohtisuoria sisäympyrän säteitä vastaan, ovat sivut sisäympyrän tangentteja. Tämä ominaisuus tekee neljäkkäästä tangentiaalisen nelikulmion. Sellaisellä nelikulmiolla on joitakin ominaisuuksia, joita voisi esitellä myös tässä.
- Pääartikkeli: Tangentiaalinen neljäkäs
Sisäympyrän sivuamispisteet jakavat sivun kahteen janaan, joita voidaan kutsua tangenttijanoiksi ti. Esimerkiksi sivulla AB on sivuamispiste J, joka jakaa sivun kahteen tangenttijanaan AJ = tA ja JB = tB. Niiden vastinjanat löytyvät muidenkin sivujen sivuamispisteiden ympäriltä, joten
kaikilla sivuilla. Tangenttijanojen pituudet saadaan laskettua suorakulmaisista kolmioista
- (kolmiosta ) ja (kolmiosta ).[10]
Tuntemalla yksi kulma ja neljäkkään sivu, voidaan nyt laskea säde
- eli
- .
Säteen suuruus voidaan laskea myös ilman kulmaa, kun on annettu vain tangenttijanojen pituudet
- .
Esimerkkejä[muokkaa | muokkaa wikitekstiä]

Eritä neljäkkäitä esiteltäessä kiinnitetään huomiota myös laatoitusongelmaan. Suunnikkailla voi laatoittaa koko tasoalueen aukottomasti, kun vastinsivut asetetaan aina vierekkäin. Neljäkkäillä on laatoituksen suhteen enemmän mahdollisuuksia, sillä sivut ovat samanpituisia. Tietyillä sisäkulman arvoilla voidaan muodostaa erilaisia kuvioita.
Neliö[muokkaa | muokkaa wikitekstiä]
Neliö on neljäkäs siinä mielessä, että sillä on neljä samanpituista sivua. Neliön sisäkulmat ovat kaikki yhtä suuret eli 90°, jolloin se on myös säännöllinen nelikulmio. Neljäkäs sanotaan usein olevan vinoon painettu neliö. Neliön lävistäjät ovat yhtä pitkät ja nekin kohtaavat toisensa kohtisuoraan pisteessä, joka jakaa lävistäjät puoliksi. Neliön sisäympyrän säde on puolet sivun pituudesta. Neliöillä laatoittaminen on varsin yksinkertaista ja neliö onkin yleisin laattamuoto.[11]
60°−120°−neljäkäs[muokkaa | muokkaa wikitekstiä]
Tämän neljäkkään pienin sisäkulma on 60° ja suurin on 120°. Lisäksi on huomattava, että 120° = 2•60°. Kun näitä neljäkkäitä latoo tasolle vierekkäin pisimmät lävistäjät linjassa, voi seuraavan rivin latoa syntyneisiin koveriin 120° koloihin. Tällä tavoin koko tason voi peittää neljäkkäillä aukottomasti. Neljäkkäät asettuvat sillä tavoin, että 60° ja 120° kulmat ovat vierekkäin. Toinen asettelutapa on sijoittaa 60° kulmat vierekkäin, jolloin syntyy sahalaitainen vaakakuvio. Laattojen väliset kolot ovat 120° suuruiset, jolloin siihen voidaan sijoittaa yksi laatta poikittain muihin nähden. Tämä kolmen laatan yhdistelmän piiri on säännöllisen kuusikulmion muotoinen. Kuusikulmiolla voi laatoittaa koko tason aukottomasti.
45°−135°−neljäkäs[muokkaa | muokkaa wikitekstiä]
Jos neljäkkään pienin sisäkulma on 45°, tulee sen viereisestä kulmasta sen suplementtikulma 180°−45° = 135°. On huomattava, että 135° = 3•45°. Tämän muotoisilla laatoilla on helppo peittää tasoalueen esimerkiksi latomalla laatat pieneimpien kulmien kärjet vastakkain vaakariviin niin, että pisimmät lävistäjät muodostavat linjan. Tämä rivin alle voi latoa toisen rivin vastaavalla tavalla. Eräs toinen syntyvä kuvio on kahdeksansakarainen tähtikuvio, jota voi laajentaa koko tason peittäväksi. Tätä neljäkästä voidaan joskus kutsua engl. Lozenge, jonka alkuperäinen merkitys on ranskaksi neljäkäs.[12][5]

Kultainen neljäkäs[muokkaa | muokkaa wikitekstiä]
Kultaisessa neljäkkäässä pisimmän lävistäjän suhde lyhyeen lävistään on kultainen leikkaus.[13]
Penrosen neljäkkäät[muokkaa | muokkaa wikitekstiä]
Penrosen neljäkkäät on kehitetty tasaisten pintojen laatoittamiseen niin, ettei toistuvaa kuviota tarvitse noudattaa. Vuorottelemalla kahta erimuotoista neljäkästä, voidaan rakentaa erilaisia useamman neljäkkään kuvioita. Kapeamman neljäkkään sisäkulmat ovat 36° ja 144° ja leveämmän ovat 72° ja 108°. Näiden neljäkkäiden eripituiset sivut suhtautuvat kuin kultainen leikkaus.[14]
Lähteet[muokkaa | muokkaa wikitekstiä]
- Väisälä, Kalle: Geometria. Porvoo: Wsoy, 1959. Teoksen verkkoversio (pdf) (viitattu 29.9.2013).
Viitteet[muokkaa | muokkaa wikitekstiä]
- ↑ Kivelä, Simo K.: Lukiotason matematiikan tietosanakirja matta.hut.fi. 10.08.2000. Viitattu 3.5.2016.
- ↑ Väisälä, Kalle: Geometria, s. 71
- ↑ Usiskin, Zalman & Griffin, Jennifer: The Classification of Quadrilaterals. A Study of Definition, Information Age Publishing, 2008, s. 55–56, (linkki sivulle 55)
- ↑ Byer, Owen & Lazebnik, Felix & Smeltzer, Deirdre: Methods for Euclidean Geometry, Mathematical Association of America, 2010, s. 53, (linkki sivulle 53)
- ↑ a b c d e Weisstein, Eric W.: Rhombus (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)
- ↑ a b Weisstein, Eric W.: Tangential Quadrilateral (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)
- ↑ Väisälä, Kalle: Geometria, s. 91–96
- ↑ Lehtinen, Matti: Geometrian perusteita (Arkistoitu – Internet Archive), s. 8
- ↑ Radić, Mirko: Some relations and properties..., s. 198, alku
- ↑ Radić, Mirko: Some relations and properties..., s. 198, kaava (3)
- ↑ Weisstein, Eric W.: Square (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)
- ↑ Weisstein, Eric W.: Lozenge (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)
- ↑ Weisstein, Eric W.: Golden Rhombus (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)
- ↑ McClure, Mark: The Rhombs (Arkistoitu – Internet Archive), The University of North Carolina at Asheville
Aiheesta muualla[muokkaa | muokkaa wikitekstiä]
- Ballew, Pat: The Origin of Rhombus (Arkistoitu – Internet Archive), sivustolta Math Words, and Some Other Words, of Interest (Arkistoitu – Internet Archive)































