Lieriö

Suora, ympyräpohjainen lieriö

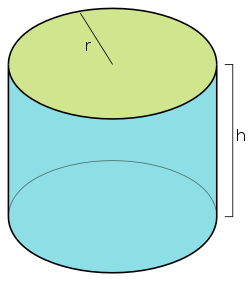
Lieriö on pinta, jonka suora muodostaa kulkiessaan umpinaista käyrää pitkin. Usein lieriöllä tarkoitetaan suoraa ympyrälieriötä (kuvassa). Tämänmuotoista kappaletta sanotaan sylinteriksi.

Tarkan määritelmän mukaan lieriö syntyy, kun tasoa, jossa on annettu yhdesti yhtenäinen alue, liikutetaan tasoon kuulumattoman vektorin suuntaan. Lieriö on tasottuva pinta, mikä tarkoittaa, että se voidaan oikaista tasoon.

Alkeisgeometriassa lieriöksi sanotaan tavallisesti kahden yhdensuuntaisen tason rajoittamaa kappaletta. Lieriön pinnan näin rajoitettua osaa sanotaan vaipaksi, pohjien keskipisteet yhdistävää janaa lieriön akseliksi ja pohjien kohtisuoraa etäisyyttä lieriön korkeudeksi. Lieriö on suora lieriö, jos sen akseli on kohtisuorassa sen pohjia vastaan.

Lieriö, jonka pohja on muodoltaan monikulmio, on särmiö eli prisma. Sen erikoistapauksia ovat muun muassa suuntaissärmiö ja suorakulmainen särmiö.

Suoran lieriön rajoittama tilavuus $V\,$ on

$V = A \cdot h \,$, missä $A\,$ on lieriön pohjan pinta-ala ja $h\,$ on lieriön korkeus

tai erityistapauksessa ympyrälieriölle

$V = \pi \cdot r^2 \cdot h\,$, missä $r\,$ on pohjaympyrän säde ja $h\,$ on korkeus.

Suoran ympyrälieriön muotoisen kappaleen kokonaispinta-ala lasketaan kaavalla

$2\pi rh+2\pi r^2 = 2\pi r(h + r) \,$, missä $2\pi rh\,$ on vaipan pinta-ala ja $2\pi r^2\,$ on kaksi kertaa pohjien pinta-ala.