Tessellaatio


Tessellaatio[1] merkitsee varsinaisesti tasopinnan peittämistä mosaiikkimaisesti tietyn muotoisilla laatoilla tai laatoiksi kutsutuilla kuvioilla siten, että laatat eivät ole osittainkaan päällekkäin eikä niiden väliin jää aukkoja. Matematiikassa tessellaation käsite voidaan yleistää myös kolmeen tai useampaankin ulottuvuuteen ja erilaisiin geometrioihin.
Jaksollisessa laatoituksessa eli tessellaatiossa sama kuvio toistuu säännöllisin välein. Yksinkertaisia tapauksia ovat säännölliset tessellaatiot, joissa laatat ovat yhteneviä säännöllisiä monikulmioita sekä puolisäännölliset (semiregulaariset) laatoitukset, joissa säännöllisiä laattoja on useamman muotoisia, mutta ne kohtaavat toisensa jokaisessa kulmassaan samalla tavalla. Jaksolliset laatoitukset voidaan ryhmitellä 17 tapettiryhmään. Laatoitusta, jossa sama kuvio ei toistu, sanotaan ei-jaksolliseksi. Aperiodisessa laatoituksessa käytetään pientä joukkoa erilaisia laattoja, jotka eivät voi muodostaa toistuvaa kuviota. Useampiulotteisessa geometriassa avaruuden täyttämistä kappaleilla tai hunajakennoilla sanotaan myös avaruuden tessellaatioksi.
Todellinen fyysinen tessellaatio on laatoitus, joka tehdään esimerkiksi sementoiduista keraamista neliöistä tai kuusikulmioita. Sellaisia käytetään usein koristekuvioina, mutta usein myös kestävinä ja vedenpitävinä pinnoitteina seinillä ja lattioilla. Historiallisesti tessellaatioita käytettiin antiikin Roomassa ja islamisessa taiteessa, esimerkiksi Alhambran palatsin koristeellisissa geometrisissa laatoituksissa. 1900-luvulla M. C. Escher käytti monissa teoksissaan taiteellisiin tarkoituksiin sekä tavallisia euklidisia että hyperboliseen geometriaan perustuvia tessellaatioita. Tessellaatioita esiintyy myös luonnossa: esimerkiksi mehiläisten hunajakennoissa esiintyy kuusikulmioista muodostuva tessellaatio.
Historia
[muokkaa | muokkaa wikitekstiä]
Tessellaatioita käyttivät jo muinaiset sumerit vuoden 4000 eaa. aikoihin rakentaessaan savitiilistä koristeellisia seiniä.[2]
Pienistä neliömäisistä laatoista tehdyt koristeelliset mosaiikkilaatoitukset, joista käytettiin nimitystä tessera, olivat antiikin aikana yleisiä.[3] Joskus niissä oli geometrisia kuviointeja.[4][5]
Vuonna 1619 Johannes Kepler tutki yhtenä ensimmäisistä tessellaatioita järjestelmällisesti. Teoksessaan Harmonices Mundi hn kirjoitti säännöllisistä ja semiregulaarisista tessellaatiosta. Hän oli mahdollisesti ensimmäinen, joka tutki ja selosti hunajakennojen ja lumihiutaleiden kuusikulmaisia muotoja.[6][7][8]

Vuonna 1891 venäläinen kristallografi Jevgraf Fjodorov todisti, että jokainen tason jasollinen laatoitus kuuluu johonkin seitsemästätoista erilaisesta isometrioiden ryhmästä.[9][10] Fjodorovin työn katsotaan useinen merkinneen tessellaatioiden matemaattisen tutkimuksen alkua. Muita alan huomattavia tutkijoita ovat olleet Shubnikov ja Belov vuonna 1964[11] sekä Heinrich Heesch ja Otto Kienzle vuonna 1963[12]
Sanan alkuperä
[muokkaa | muokkaa wikitekstiä]Latinassa sana tessella tarkoittaa pientä kuutiomaista saven, kiven tai lasin palasta, jota voidaan käyttää mosaiikkeihin.[13] Alun perin sana tarkoittaa pientä neliötä ja johtuu neliötä tarkoittavasta sanasta tessera, joka aikoinaan lainattiin latinaan kreikasta ja on johdos kreikan kielen lukusanasta τέσσερα, neljä. Merkitykseltään sana vastaa arkikielen sanaa laatoitus, jolla viitataan tessellaatioiden usein lasitetusta savesta valmistettuihin sovelluksiin.
Yleiskatsaus
[muokkaa | muokkaa wikitekstiä]Kaksiulotteinen tessellaatio eli laatoitus on geometrian haara, joka tutkii sitä, miten laatoiksi kutsutut muodot voidaan järjestää annettujen sääntöjen mukaan siten, että niiden väliin ei jää aukkoja. Nämä säännöt voidaan vaihdella. Tavallisimmin edellytetään, että laattojen väliin ei jää aukkoja eikä minkään laatan kärki sijaitse keskellä toisen laatan sivua.[14] Esimerkiksi tiiliä yhteen muurattaessa käytetyt limitykset eivät viimeksi mainittua ehtoa täytä. Sen sijaan esimerkiksi jäljempänä käsitellyt säännölliset tessellaatiot täyttävät tämän ehdon.
Säännölliset tessellaatiot
[muokkaa | muokkaa wikitekstiä]Säännöllinen tessellaatio on laatoitus, jossa taso täytetään yhtenevillä säännöllisillä monikulmioilla ja jossa jokaisessa kärkipisteessä, joissa laatat kohtaavat toisensa, niiden sivut muodostavat yhtä suuret kulmat.[15] Ainoat säännölliset monikulmiot, joista tällainen laatoitus voidaan muodostaa, ovat tasasivuiset kolmiot, neliöt ja säännölliset kuusikulmiot. Kutakin niistä voidaan sijoittaa yhtenevinä kopiona tasoon loputtomasti niin, että ne peittävät koko tason.[7] Neliöistä muodostuva säännöllinen tessellaatio on samanlainen yksinkertainen ruudukko, joka esiintyy esimerkiksi tavallisella ruutupaperilla.
Muita tessellaatioita
[muokkaa | muokkaa wikitekstiä]

Jos asetettuja vaatimuksia muutetaan, tessellaatioita voidaan muodostaa hyvin monen tyyppisiä. Esimerkiksi on olemassa neljä tyyppiä puolisäännöllisiä tessellaatioita, jotka muodostuvat useammasta kuin yhdestä lajista säännöllisiä monitahokkaita mutta joissa monikulmiot silti kohtaavat toisensa samalla tavalla joksisessa kärjessä.[16] Epäsäännöllisiä tessellaatiota voidaan tehdä myös esimerkiksi viisikulmioista, polyominoista ja melkein mistä tahansa geometrisista muodoista. Taiteilija M. C. Escher tuli kuuluisaksi epäsäännöllisten kuvioiden muodostamista tessellaatioista, joiden laatat olivat usein eläinten tai muiden luonnon kohteiden muotoisia.[17] Valitsemalla eri muotoisille laatoille eri värejä voidaan saada aikaan hyvinkin erikoisia kuvioita, joilla voidaan koristella fyysisiä pintoja kuten kirkkojen lattioita.[18]
Matemaattinen käsittely
[muokkaa | muokkaa wikitekstiä]Matemaattisesti tessellaatio eli laatoitus voidaan määritellä euklidisen tason peitteeksi, joka muodostuu numeroituvasta määrästä laatoiksi sanottuja suljettuja joukkoja, jotka leikkaavat toisensa vain reunoillaan. Nämä laatat voivat olla monikulmioita tai muun muotoisia. Yleensä kuitenkin edellytetään, että ne ovat homeomorfisia suljetun kiekon kanssa, eivät siis esimerkiksi äärettömän laajoja alueita tai alueita, joissa on reikä keskellä.[19]
Monissa tessellaatioissa on vain äärellinen määrä laatan perustyyppejä, joista yhden kanssa kaikki laatat ovat yhteneviä. On myös mahdollista, että tessellaation kaikki laatat ovat keskenään yhteneviä. Jos jotakin geometrista muotoa voidaan käyttää tällaisena laatan perustyyppinä, jonka kopioilla voidaan peittää koko taso, sanotaan, että muoto tesselloi tai laatoittaa tason.
Ei tunneta yleistä sääntöä, jolla voitaisiin kaikissa tapauksissa ratkaista, voidaanko taso laatoittaa annetun muotoisilla laatoilla.[19] On kuitenkin helppo todistaa, että minkä tahansa muotoisilla kolmioilla, muillakin kuin tasasivuisilla, samoin kuin millä tahansa nelikulmioilla voidaan laatoittaa taso.[20] Conwayn kriteeri on eräs riittävä, mutta ei välttämätön edellytys sille, että annettu muoto laatoittaa tason jaksollisesti ilman, että sitä tarvitsee missään muuntaa peilikuvakseen.[21]
Monikulmioista muodostuville tessellaatiolle on käytössä useita merkitätapoja. Säännöllisistä monikulmioista muodostuville tessellaatiolle yleisin merkintä on kärkikonfiguraatio, joka on luettelo kärjen ympärillä olevien monikulmion sivujen lukumääristä. Esimerkiksi tavallinen neliöruudukko merkitään 4.4.4.4 tai 44. Säännöllisistä kuusikulmioista koostuva laatoitus merkitään 6.6.6 tai 63.[19]
Tessellaatioon liittyviä käsitteitä
[muokkaa | muokkaa wikitekstiä]Matematiikassa tessellaatioihin liittyy useita teknisiä termejä. Särmä on kahden vierekkäisen laatan yhteisten pisteiden joukko eli leikkaus, joka usein on jana. Kärki on kolmen tai useamman laatan yhteinen piste. Näitä termejä käyttäen isogonaalinen eli kärkitransitiivinen laatoitus määritellään laatoitukseksi, jonka kaikki kärkipisteet ovat samanlaisia, toisin sanoen monikulmiot järjestyvät jokaisen kärjen ympärille samalla tavalla.[19] Perusalue (engl. fundamental region) on muoto, esimerkiksi suorakulmio, joka toistumisesta tessellatio muodostuu.[22] Esimerkiksi tavallisessa neliöistä muodostuvassa ruudukossa perusalueet ovat neliöitä, ja niitä on neljä jokaisen kärjen ympärillä.[19]
Monikulmioiden sivut eivät välttämättä ole samoja kuin laattojen särmät. Esimerkiksi tavallisen tiiliseinän kaltaisessa laatoituksessa näin ei ole, koska jokaisen suorakulmaisen tiilen pitkä sivu rajoittuu kahteen sen ylä- tai alapuolella olevaan tiileen.[19]
Tessellaatioiden luokittelua
[muokkaa | muokkaa wikitekstiä]Normaali laatoitus on tessellaatio, jossa jokainen laatta on topologisesti ekvivalentti kiekon kanssa, kahden laatan leikkaus on joko yhtenäinen pistejoukko tai tyhjä joukko, ja kaikki laatat ovat tasaisesti rajoitettuja. Tämä merkitsee, että vaikka laatat saattavatkin olla eri kokoisia, on olemassa yläraja, jota suurempi yksikään laatta ei pisimmältä halkaisijaltaan ole, sekä myös alaraja, jonka säteinen ympyrä mahtuu minkä tahansa laatan sisään.[23]

Monoedrinen laatoitus on tessellaatio, jossa kaikki laatat ovat yhteneviä. Sillä on siis vain yksi peruslaatta. Yhden erityisen mielenkiintoisen monoedristen tessellaatioiden tyypin muodostavat spiraaliset monoedriset laatoituksen. Ensimmäisen spiraalisen monoedrisen laatoituksen keksi Heinz Voderberg vuonna 1936. Tämän Voderbergin laatoituksen peruslaatta on ei-kupera yhdeksänkulmio.[2]



Monedrinen laatoitus on isoedrinen, jos siinä kaikki laatat kuuluvat samaan transitiivisuusluokkaan, toisin sanoen jokainen laatta voidaan siirtää minkä tahansa toisen laatan paikalle tasoa pitkin yhdensuuntaissiirroilla ja rotaatiolla kääntämättä sitä peilikuvakseen.[23] Jos peruslaatta on sellainen, että sillä voidaan laatoittaa taso, mutta mikään laatoitus on ei ole isoedrinen, peruslaattaa sanotaan anisoedriksesi ja se muodostaa anisoedrisia laatoituksia. Tällöin osa laatoista on peruslaatan peilikuvia.
Säännöllinen tessellaatio on hyvin symmetrinen laatoitus, jossa kaikki laatat ovat samanlaisia säännöllisiä monikulmioita ja joissa minkään laatan kärki ei ole keskellä toisen laatan sivua. Sellaisia laatoituksia on vain kolme, joista yksi muodostuu tasasivuisista kolmioista toinen neliöistä ja kolmas säännöllisistä kuusikulmioista.[24] Nämä kaikki kolme laatoitusta ovat isogonaalisia ja monoedrisiä.
Semiregulaarinen eli Arkhimedeen tessellaatio sisältää useampaa kuin yhtä tyyppiä säännöllisiä monikulmioita isogonaalisessa järjestyksessä. Erilaisia semiregulaarisia tessellaatioita on kahdeksan (tai yhdeksän, jos laatoitukset, jotka ovat toistensa peilikuvia, lasketaan kahdeksi eri tesellaatioksi.)[25] Ne voidaan esittää kärkikonfiguraatioilla; esimerkiksi neliöistä ja säännöllisistä kahdeksankulmioista muodostva semiregulaarinen tessellaatio merkitään 4.82, koska jokaisessa kärjessä toisensa kohtaa yksi neliö ja kaksi kahdeksankulmiota.[26]
Särmätessellaatiossa jokainen laatta voidaan peilata jonkin sivunsa suhteen niin, että se tarkalleen osuu viereisen laatan päälle. Sellaisia ovat esimerkiksi tasasivuisista tai tasakylkisistä kolmioista muodostuvat laatoitukset.[27]
On olemassa myös suuri joukko laatoituksia, joissa jonkin monikulmion kärki on toisen monikulmion sivulla sijaitsematta sen kärjessä. Sellaisia ovat esimerkiksi pythagoralaiset laatoitukset, jotka koostuvat kahden kokoisista neliöistä ja joissa jokainen suuri neliö koskettaa neljää pientä neliötä ja päinvastoin.[28]

Tapettiryhmät
[muokkaa | muokkaa wikitekstiä]Laatoitukset, joilla on siirtosymmetriaa kahdessa toisistaan riippumattomassa suunnassa, voidaan luokitella tapettiryhmiin, joita on kaikkiaan 17.[29] On väitetty, että kaikki nämä 17 ryhmää ovat edustettuina Alhambran palatsissa Granadasa, Espanjassa. Vaikka tämä on kiistanalaista[30], Alhambran laatoistusten monimuotoisuus ja kehittyneisyys on yllättänyt nykyiset tutkijat.[31] Kolmesta säännöllisestä laatoituksesta kaksi kuuluu tapettiryhmään p6m, kolmas ryhmään p4m.
Kaksiulotteiset laatoitukset, joilla on symmetria vain yhteen suuntaan, voidaan vastaavasti luokitella seitsemään friisiryhmään, jotka kuvaat mahdollisia friisimalleja.[32]
Jaksottomat laatoitukset
[muokkaa | muokkaa wikitekstiä]
Penrosen laatoitukset, jotka koostuvat kahdesta erilaisesta nelikulmaisesta protolaatasta, ovat tunnetuin esimerkki laatoista, joilla saadaan aikaan vain ei-jaksollisia laatoituksia. Tällaiset laatoitukset kuuluvat jaksottomien eli aperiodisten tessellaatioiden luokkaan. Jaksottomia laatoituksia voidaan saada aikaan rekursiivisella prosessilla. Erään luokan sellaisia laatoituksia muodostavat Pinwheelin laatoitukset, joissa laatat esiintyvät äärettömän monessa eri asennossa.[33]
Jaksottomilla laatoituksilla ei ole siirtosymmetriaa, mutta muita symmetriaominaisuuksia niillä kyllä voi esiintyä. Niissä sama laatoituksen rajoitettu osa saattaa toistua äärettömän montakin kertaa, minkä lisäksi niiden symmetriat saattavat muodostaa äärellisiä rotaatioiden ja peilausten ryhmiä.[34] Jotkut Penrosen mallit voidaan muodostaa korvaussäännöillä, joissa käytetään rombeiksi nimitettyjen laattojen kokoelmia ja jotka havainnollistavat skaalaussymmetriaa.[35]

Wangin laatat ovat neliöitä, jotka on värjätty jokaiselta sivultaan ja sijoitettu niin, että vierekkäisten neliöiden toisiaan koskettavat sivut ovat samanvärisiä. Tämän sijoittelun vuoksi niitä sanotaan joskus myös Wangin dominoiksi. On mahdollista muodostaa sellainen joukko Wangin dominoita, että niillä voidaan laatoittaa taso, mutta vain aperiodisesti. Tämä tiedetään, koska on osoitettu, että jokainen Turingin kone voidaan kuvata joukolla Wangin dominoita, mutta niillä koko taso voidaan laatoittaa, jos ja vain jos kyseinen Turingin kone ei pysähdy. Koska on todistettu, ettei ole sellaista algoritmia, jolla pysähtymisongelma voitaisiin kaikissa tapauksissa ratkaista, ei ole myöskään sellaista algoritmia, jolla voitaisiin kaikissa tapauksissa selvittää, voidaanko annetulla joukolla Wangin dominoita laatoittaa koko taso.[36][37][38][39][40]

Truchet'n laatat ovat neliömäisiä laattoja, jotka on kuvioitu niin, ettei niillä ole kiertosymmetriaa. Vuonna 1704 Sébastien Truchet käytti neliömäistä laattaa, joka oli jaettu kahteen eriväriseen kolmioon. Tällaisilla laatoilla taso on mahdollista täyttää sekä jaksollisesti että satunnaisesti.[41][42]
Tessellaatiot ja väritys
[muokkaa | muokkaa wikitekstiä]
Joskus laatan värin katsotaan kuuluvan oleellisena osana laatoitukseen; toisissa yhteyksissä värillä ei katsotan olevan merkitystä. Kun laatoitus on esitetty monivärisenä, onkin yksiselitteisyyden vuoksi mainittava, kuuluvatko värit laatoitukseen vai onko niitä käytetty vain selvyyden vuoksi, toisin sanoen, ovatko saman muotoiset mutta eri väriset laatat katsottava identtisiksi, mikä vaikuttaa laatoituksen symmetriaominaisuuksiin. Normaalissa euklidisessa tasossa neljän värin lause osoittaa, että jokainen laatta voidaan värittää yhdellä värillä niin, että mitkään laatat, jotka koskettavat toisiaan muutoinkin kuin vain kulmittain yhdessä pisteessä, eivät ole samanvärisiä. Väritys neljällä värillä ei kuitenkaan aina säilytä laatoituksen kaikkia symmetrioita. Jos värityksen halutaan ne säilyttävän, saatetaan eräissä tapauksissa tarvita seitsemääkin väriä, kuten oheisen kuvan mukaisten suorakulmioiden tapauksessa.[43]
Tessellatiot monikulmioilla
[muokkaa | muokkaa wikitekstiä]
Paitsi säännöllisillä monikulmioilla, on tutkittu myös laatoituksia muunlaisilla monikulmioilla.
Mitä tahansa kolmiota tai nelikulmiota, myös ei-kuperaa, voidaan käyttää peruslaattana, jolloin koko taso voidaan täyttää sen kanssa yhtenevillä laatoilla, monessa tapauksessa useammallakin tavalla.[20] Minkä tahansa nelikulmion kopioista voidaan muodostaa tessellaatio, jolla on siirtosymmetria ja lisäksi rotaatiosymmetria sellaisten 180 asteen kiertojen suhteen, joiden keskuksia ovat nelikulmion sivujen keskipisteet. Jos nelikulmio on epäsymmetrinen, näin saatu laatoitus kuuluu tapettiryhmään p2. Perusalueena on kyseinen nelikulmio.
Säännöllisillä viisikulmiolla tasoa ei voi laatoittaa, koska niissä vierekkäisten sivujen välinen kulma on 108 astetta, eikä 360 astetta (täysi kulma) jaettuna tällä luvulla ole kokonaisluku.[44] Tunnetaan kuitenkin viisitoista erityyppistä epäsäännöllistä viisikulmiota, joilla se on mahdollista. Niistä viisi ensimmäistä keksi saksalainen matemaatikko Karl Reinhardt vuonna 1918. Myöhemmin on keksitty joukko muitakin, viimeksi Casey Mannin vuonna 2015 tietokonegrafiikan avulla löytämä. Ei ole pystytty todistamaan, ovatko jo löydetyt 15 viisikulmiota ainoat, joilla se on mahdollista, vai onko sellaisia vielä muitakin.[45]
Reinhardt osoitti myös, että yhtenevillä kuusikulmioilla taso voidaan laatoittaa vain, jos kuusikulmio kuuluu johonkin kolmesta sen mittasuhteiden perusteella määriteltävistä luokasta. Jos kuusikulmion kulmia merkitään kirjaimilla A, B, C, D, E ja F ja sivuja kirjaimilla a, b, c, d, e, f, tessellaatio on mahdollinen, jos ja vain jos kuusikulmio toteuttaa ainakin yhden seuraavista ehdoista:
- A + B + C = 360° ja a = d,
- A + B + D = 360°, a = d ja c = e tai
- A = C = E = 120°, a = b, c = d ja e = f.
Säännöllinen kuusikulmio täyttää kaikki nämä ehdot, joten se kuuluu kaikkiin niiden määrittämiin luokkiin.[20]
On todistettu, että millään yhtenevillä kuperilla monikulmioilla, joissa on enemmän kuin kuusi sivua, ei tasoa voi täyttää. Joillakin ei-kuperilla monikulmioilla se sen sijaan on mahdollista.[20]
Voronoin laatoitus
[muokkaa | muokkaa wikitekstiä]Voronoin tai Dirichletin laatoitukset ovat laatoituksia, joissa jokainen laatta määritellään niiden pisteiden joukoiksi, jotka ovat lähempänä jotakin annettuun diskreettiin pistejoukkoon kuuluvaa pistettä kuin mitään muuta. Tätä voidaan verrata maantieteellisiin alueisiin, joista kukin on määritelty alueeksi, joka on lähempänä jonkin kaupungin keskustaa kuin minkään muun.[46][47] Jokaista tällaista määrittelevää pistettä ympäröivä Voronoin solu on kupera monikulmio.
Delaunayn triangulaatio on tessellaatio, joka on Voronoin laatoituksen duaaligraafi. Delaunayn triangulaatiot ovat hyödyllisiä numeerisissa simulaatioissa muun muassa sen vuoksi, koska niissä pienimmät sivujen väliset kulmat ovat suurempia kuin missään muussa annettujen pisteiden avulla muodostettavassa triangulaatiossa. [48] Satunnaisesti sijoiteltujen pisteiden määrittämiä Voronoin laatoituksia voidaan käyttää muodostamaan tasoon satunnainen laatoitus.[49]

Pallopinnan tessellaatiot ja Schwarzin kolmiot
[muokkaa | muokkaa wikitekstiä]Tessellaatioita voidaan muodostaa, paitsi tasolle, myös pallon pinnalle. Pallokolmioita, joilla se on mahdollista, sanotaan Schwarzin kolmioiksi.[50][51]
Tessellaatiot kolmiulotteisessa avaruudessa
[muokkaa | muokkaa wikitekstiä]
Vastaavalla tavalla kuin tasossa voidaan tessellaatio määritellä myös kolmiulotteisessa avaruudessa. Tessellaatioita kolmessa tai useammassa ulottuvuudessa sanotaan myös hunajakennoiksi
On olemassa joukko monitahokkaita, jotka voidaan pinota niin, että ne täyttävät kolmiulotteisen tilan aukottomasti. Niitä sanotaan paralleloedreiksi[52] eli plesioedreiksi, ja niissä tahkojen lukumäärä vaihtelee 4:stä 38:een.[53] Säännöllisistä monitahokkaista eli Platonin kappaleista kuutio on kuitenkin ainoa, jolla tila voidaan täyttää aukottomasti.[44] Aristoteles tosin väitti asiaa mitenkään todistamatta, että tila voitaisiin täyttää myös säännöllisillä tetraedreilla, ja niin uskottiinkin yleisesti siihen saakka, kunnes Johannes Regiomontanus 1400-luvulla osoitti, ettei se ole mahdollista.[52]
Muita monitahokkaita, joilla tila voidaan täyttää, ovat kolmi-, neli- ja kuusikulmaiset särmiöt, rombidodekaedri, kahdeksan neljäkkään ja neljän kuusikulmion rajoittama 12-tahokas sekä katkaistu oktaedri.[54]
Kysymys siitä, millaisia säännöllisiä kolmiulotteisia tessellaatioita on olemassa, liittyy läheisesti siihen, minkälaiset säännölliset kidehilat ovat mahdollisia. Kiteisen aineen kidehila voidaan nimittäin käsittää kolmiulotteiseksi tessellaatioksi, jonka laattoja ovat jokaisen atomin ympärillä ne avaruuden alueet, jotka ovat lähempänä kyseisen atomin ydintä kuin minkään muun atomin ydintä.[52] Näitä alueita, jotka samalla ovat paralleloedreja, sanotaan Wigner–Seitzin soluiksi.[52] Esimerkiksi yksinkertaisessa kuutiollisessa kidehilassa ne ovat kuutioita, pintakeskisessä kuutiollisessa hilassa rombidodekaedreja.[55]
Tunnetaan myös aineita, joiden atomit ovat järjestyneet jaksottomasti eli niissä ei ole samanlaisina toistuvaa yksikkökoppia mutta kuitenkin selviä symmetrisiä rakenteita. Niitä sanotaan kvasikiteiksi, ja niitä voidaan pitää Penrosen laattojen kolmiulotteisina vastineina.[56][57]
Vaikka tilaa ei voida täyttää pelkillä säännöllisillä tetraedreillä eikä pelkillä säännöllisillä oktaedreillä, voidaan kuitenkin muodostaa semiregulaarinen hunajakenno, jossa jokaista kärkipistettä ympäröi kahdeksan tetraedriä ja kahdeksan oktaedriä. On olemassa myös kvasisäännöllisiä hunajakennoja, jotka koostuvat sellaista monitahokkaista, jotka eivät ole säännöllisiä mutta joiden sivut ovat säännöllisiä monikulmioita. Sellaisia ovat esimerkiksi särmiöt, joiden pohjana on tasasivuinen kolmio tai säännöllinen kuusikulmio.[58]
Schmittin-Conwayn kaksoisprima on esimerkki kuperasta monitahokkaasta, jonka kopioilla tila voidaan täyttää, mutta vain jaksottomasti.[59]
Tessellaatiot epäeuklidisissa geometrioissa
[muokkaa | muokkaa wikitekstiä]

Tessellaatiot ovat mahdollisia myös epäeuklidisissa geometrioissa kuten hyperbolisessa geometriassa. Hyperbolisen tason uniformisessa laatoituksessa, joka voi olla säännöllinen, kvasisäännöllinen tai semiregulaarinen, laatat ovat säännöllisiä monikulmioita, jotka koskettavat toisiaan reunoillaan. Ne ovat kärkitransitiivisia ja isogonaalisia, toisin sanoen on aina olemassa yhtenevyyskuvaus, jolla mikä tahansa kärki voidaan kuvata mille tahansa toiselle.[60][61]
Hyperbolisen avaruuden uniforminen hunajakenno on uniforminen tessellaatio, jonka kaikki solut ovat uniformisia monitahokkaita, toisin sanoen niiden kaikki tahkot ovat säännöllisiä monikulmioita ja ne voidaan aina kuvata yhtenevyyskuvauksella itselleen niin, että mikä tahansa kärki kuvautuu mille tahansa toiselle. Kolmiulotteisessa hyperbolisessa avaruudessa on yhdeksän Coxeterin ryhmiin liittyvää perhettä kuperia uniformisia hunajakennoja, jotka voidaan muodostaa Wythoffin konstruktiolla. Niitä voidaan kuvata permutoimalla kunkin perheen Coxeterin diagrammin renkaita.[62]
Kuvia
[muokkaa | muokkaa wikitekstiä]-
Floret'n viisikulmainen laatoitus, semiregulaarisen laatoituksen duaali ja yksi viidestätoista viisikulmioiden muodostamista laatoituksista.
-
Vorderbergin laatoitus on yhdeksänkulmioista muodostuva spiraalimainen monoedrinen laatoitus.
-
Vuorotteleva kahdeksankulmainen tai tritetragonaalinen laatoitus on eräs hyperbolisen tason uniforminen laatoitus.
Tessellaatiot taiteessa
[muokkaa | muokkaa wikitekstiä]
Arkkitehtuurissa tessellaatioita on ikivanhoista ajoista käytetty koristeaiheina. Mosaiikkilaatoitukset on usein geometrisesti muotoiltu.[5] Myöhäisemmissä kulttuureissa on käytetty myös aikaisempia suurempia laattoja joko sellaisenaan tai jokainen eri tavalla koristeltuina. Kaikkein koristeellisimpiin kuuluvat monet islamilaisen arkkitehtuurin luomukset varsinkin maurilaiset Girih- ja Zellige-seinälaatoitukset Alhambrassa[63] ja Córdoban moskeijassa.[64]
Tessellaatiot esiintyvät säännöllisesti M. C. Escherin taiteessa. Hänen suoraisina esikuvinaan olivat maurilaisten aikaansaannokset muun muassa Alhambrassa, jossa hän kävi vuonna 1936.[65] Teoksessaan Circle Limit III hän käytti selvästi hyperboliseen geometriaan viittaavaa tessellaatiota.[66][67] Puupiirrostaan Circle Limit IV varten Escher tutki lyijykynän ja musteen avulla tarvittavaa geometriaa.[68] Escher selitti, että sarja nousee rakettien tavoin äärettömän kaukaiselta rajaviivalta, jota kohti se lopulta myös palaa, mutta ettei yksikään sarjan jäsen koskaan tavoita rajaviivaa.[69]
Tesselloidut kuvioinnit ovat hyvin yleisä erilaisissa tekstiileissä, olivatpa ne kudottuja, ommeltuja tai painettuja. Niitä esiintyy niin matoissa, ryijyissä, tapeteissa kuin päiväpeitteissäkin. Tessellaatiot muodostavat yhden keskeisen tyypin myös paperia taittelmalla valmistetuissa origameissa.[70]
Teollisuudessa
[muokkaa | muokkaa wikitekstiä]Tessellaatiota käytetään laajalti tuotantotekniikassa, jotta materiaali saataisiin mahdollisimman tarkoin käytetyksi hyödyksi eikä sitä menisi hukkaan. Näin tehdään esimerkiksi, kun pellistä on leikattava suuri määrä saman muotoisia osia esimerkiksi auton ovia tai juomatöllejä varten.[71]
Tessellaatiota muistuttavia rakenteita muodostuu myös, kun ohut kalvo murtuu ja syntyy samantapaisia kuvioita kuin liejun tai märän saven kuivuessa.[72][73]. Mikro- ja nanoteknologian avulla näissä voidaan havaita jonkin asteista itseorganisoitumista.[74]
Luonnossa
[muokkaa | muokkaa wikitekstiä]



Hunajakenno kuusikulmaisine soluineen on tunnettu esimerkki tessellaatiosta luonnossa.[75]
Kasvikunnassa ruutukuvioita tai muita tesselloituneita kuvioita esiintyy esimerkiksi joidenkin kukkien terälehdissä, puun kuoressa ja hedelmissä. Tunnettuja kasveja, joiden terälehdissä on tällaisia kuvioita, ovat pikarililjat (Fritillaria)[76] ja jotkut myrkkyliljalajit (Colchicum).[77]
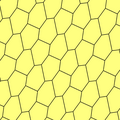
Luonnossa esiintyy monenlaisia kuvioituja muotoja, jotka ovat syntyneet ohuina kalvoina esiintyvien aineiden halkeillessa. Tällaisia muotoja voidaan kuvailla Gilbertin tessellaatioina[78]. Gilbertin tessellaatio on saaneet nimensä Edgar Gilbertin mukaan, ja se on matemaattinen malli sille, miten kuivuvaan saveen muodostuvat kuviot, neulamaiset kiteet ja muut samantapaiset rakenteet muodostuvat. Sen mukaan halkeamat voivat aluksi syntyä satunnaisesti tason eri kohtiin, mutta jokainen halkeama leviää kahteen vastakkaiseen suuntaan alkujaan satunnaisesti valikoituneesta lähtöpisteestään, jolloin halkeamien kohdatessa toisena syntyy epäsäännöllisten kuperien monikulmioiden muodostama tessellaatio.[79] Basalttiset laavavirrat jähmettyvät usein selvästi toisistaan erottuvien pylväiksi muodostamiksi kuvioiksi, kun ne jäähtyessään kutistuvat. Syntyvät kuviot muodostavat usein kuusikulmaista tessellaatiota vastaavan rakenteen. Sellainen on esimerkiksi Giant’s Causeway Pohjois-Irlannissa.[80] Joskus kallio saattaa haljeta lähes suorakulmaisiksi lohkareiksi, niin että syntyy tesselloitunut kiveys. Tällainen harvinainen muodostuma on löydetty esimerkiksi Eaglehawk Neckistä Tasmaniasta.[81]
Tesselloituneita muotoja esiintyy myös vaahdossa. Vaahtokuplat pakkautuvat Plateaun lain mukaisesti niin, että niiden yhteenlaskettu pinta-ala on pienin mahdollinen. Näihin liittyy kysymys siitä, miten kuplat tai kappaleet voidaan pakata mahdollisimman tiiviisti. Vuonna 1887 lordi Kelvin esitti, että tiivein pakkaus muodostuu vain yhdenlaisista kappaleista, katkaistuista oktaedreistä, joiden pinnat ovat vain hieman kaarevia. Vuonna 1993 Denis Weaire ja Robert Phelan ehdottivat Weairen-Phelanin rakenneta, jossa tilavuudeltaan yhtä suuret kuplat erottaa pienempi rajapinta-ala kuin Kelvinin vaahdossa.[82]
Pulmatehtävissä ja ajanvietematematiikassa
[muokkaa | muokkaa wikitekstiä]
Tessellaatiot ovat antaneet aihetta monenlaisiin pulmatehtäviin, alkaen perinteisistä palapeleistä, jotka koostuvat epäsäännöllisen muotoisista puu- tai pahvipaloista[83] ja tangramista[84] aina nykyaikaisempiin tehtäviin saakka, joilla usein on matemaattinen perusta. Esimerkiksi polyiamondit ovat tasasivuisista kolmioista ja polyominot neliöistä koostuvia kuvioita, joita käytetään monissa laatoituspulmatehtävissä.[85][86] Muun muassa Henry Dudeney ja Martin Gardner ovat käyttäneet tessellaatioita monin tavoin ajanvietematematiikassa. Dudeney keksi muun muassa saranoidun dissektion[87], kun taas Gardner kirjoitti rep-tiilestä, kuviosta, joka voidaan jakaa pienempiin alkuperäisen kanssa yhdenmuotoisiin osiin.[88][89] Gardnerin Scientific American -lehdessä julkaisemien artikkelien innoittamana amatöörimatemaatikko Marjorie Rice keksi neljä uutta viisikulmioista muodostuvaa tessellaatiota.[90][91]
Neliön neliöiminen on tehtävä, jossa neliö, jonka sivujen pituudet ovat kokonaislukuja, on täytettävä pienemmillä neliöillä, joiden niidenkin sivujen pituudet ovat kokonaislukuja.[92][93] Sen yleistyksenä voidaan pitää tason neliöintiä, jossa se peitetään neliöillä, joiden sivuina ovat kaikki luonnolliset luvut ilman, että mikään niistä toistuu. James ja Frederick Henle ovat todistaneet, että se on mahdollista.[94]
Lähteet
[muokkaa | muokkaa wikitekstiä]- Martin Gardner: Penrose Tiles to Trapdoor Ciphers. Cambridge University Press, 1989. ISBN 978-0-88385-521-8.
- Branko Grünbaum, G. C. Shephard: Tilings and Patterns. W. H. Freeman, 1987. ISBN 0-7167-1193-1.
- Wilhelm Magnus: Noneuclidean Tesselations and Their Groups. Academic Press, 1974. ISBN 978-0-12-465450-1.
Viitteet
[muokkaa | muokkaa wikitekstiä]- ↑ Matematiikan verkkosanakirja Matematiikkalehti Solmu. Viitattu 27.9.2018.
- ↑ a b Clifford A. Pickover: The Math Book: From Pythagoras to the 57th Dimension, 250 Milestones in the History of Mathematics, s. 372. Sterling, 2009. ISBN 9781402757969.
- ↑ Katherine M. D. Dunbabin: Mosaics of the Greek and Roman world, s. 280. Cambridge University Press, 2006.
- ↑ The Brantingham Geometric Mosaics Hull Museum. Viitattu 27.9.2018.
- ↑ a b Robert Field: Geometric Patterns from Roman Mosaics. Tarquin, 1988. ISBN 978-0-906-21263-9.
- ↑ Johannes Kepler: Harmonices Mundi. {{{Julkaisija}}}, 1619.
- ↑ a b Jan Gullberg: Mathematics from the Birth of Numbers, s. 395. Norton, 1997. ISBN 0-393-04002-X.
- ↑ Ian Stewart: What Shape is a Snowflake, s. 13. Weldenfeld and Nicholson, 2001. ISBN ISBN 0-297-60723-5.
- ↑ Hristo Djidjev, Miodrak Potkonjak: ”Historic Picture: Coverage and Tessellation”, Dynamic Coverage Problems in Sensor Networks, s. 2. Los Alamos National Laboratory, 2012. Teoksen verkkoversio.
- ↑ Jevgraf Fjodorov: Simmetrija na ploskosti. Zapiski Imperatorskogo Sant-Petersburgskogo Mineralogicheskogo Obshchestva, 1891, nro 28, s. 245–291. (venäjäksi)
- ↑ Aleksei Vasilʹevich Shubnikov, Nikolai Vasilʹevich Subnikov Belov: Colored Symmetry. Macmillan, 1964. Teoksen verkkoversio.
- ↑ H. Heesch, O. Kielzle: Flächenschluss: System der Formen lückenlos aneinanderschliessender Flächteile. Springer, 1963. (saksaksi)
- ↑ Tessellate Merriam-Webster Online. Viitattu 27.9.2018.
- ↑ R. Conway, H. Burgiel, G. Goodman-Strauss: The Symmetries of Things. Peters, 2008.
- ↑ H. S. M. Coxeter: ”Regular Tessellations”, Regular Polytopes, 3. painos, s. 58–59. Dover: {{{Julkaisija}}}, 1973..
- ↑ Rollett Cundy: Mathematical Models (2. painos), s. 61–62. Oxford, 1961.
- ↑ J. L. Locher (toim.): The World of M. C. Escher, s. 11–12, 15–16. Abrams, 1974. ISBN 0-451-79961-5.
- ↑ Basilica di San Marco: Tessellated floor Basilica di San Marco. Viitattu 27.9.2018.
- ↑ a b c d e f Branko Grünbaum, Geoffrey Colin Shephard: Tilings and Patterns, s. 59. New York: W. H. Freeman, 1987.
- ↑ a b c d Malcolm E. Lines: ”Lattialaatoista kvasikiteisiin”, Jättiläisten harteilla: matematiikan heijastuksia luonnontieteisiin, s. 107–113. Suomentanut Veli-Pekka Ketola. Art House, 2000. ISBN 951-884-285-X.
- ↑ Doris Schattschneider: Will It Tile? Try the Conway Criterion!. Mathematics Magazine, Syyskuu 1980, 53. vsk, nro 4, s. 224–233.
- ↑ Michele Emmer, Doris Schattschneider: M.C. Escher's Legacy: A Centennial Celebration, s. 325. Springer Berlin Heidelberg, 2007. ISBN 978-3-540-28849-7. Teoksen verkkoversio.
- ↑ a b Clare E. Horne: Geometric Symmetry in Patterns and Tilings, s. 172, 175. Woodhead Publishing, 2000. ISBN 9781855734920.
- ↑ Regular Tessellation Wolfram MathWorld. Eric W. Weisstein. Viitattu 27.9.2018.
- ↑ Ian Stewart: What Shape is a Snowflake, s. 75. Weldenfeld and Nicholson, 2001. ISBN ISBN 0-297-60723-5.
- ↑ Schläfli Tessellations 1997–2012. University of Cambridge. Viitattu 27.9.2018.
- ↑ Matthew Kirby, Ronald Umble: Edge Tessellations and Stamp Folding Puzzles. Mathematics Magazine, 2011, 84. vsk, nro 4, s. 283–289. doi:10.4169/math.mag.84.4.283.
- ↑ David Wells: ”Two squares tessellation”, The Penguin Dictionary of Curious and Interesting Geometry, s. 260–261. New York: Penguin Books, 1991. ISBN 0-14-011813-6.
- ↑ M. A. Armstrong: Groups and Symmetry. Springer-Verlag, 1988. ISBN 978-3-540-96675-3.
- ↑ Branko Grünbaum: What symmetry groups are present in the Alhambra?. Notices of the American Mathematical Society, 2006, 53. vsk, nro 6, s. 670–673. Artikkelin verkkoversio.
- ↑ Peter J. Lu, Steinhardt: Decagonal and quasi-crystalline tilings in medieval Islamic architecture. Science, 23.2.2007, 315. vsk, nro 5815, s. 1106–1110. doi:10.1126/science.1135491.
- ↑ Frieze Group Wolfram MathWorld. Eric W. Weisstein. Viitattu 27.9.2018.
- ↑ C. Radin: The Pinwheel Tilings of the Plane. Annals of Mathematics, Toukokuu 1994, 139. vsk, nro 3, s. 661–702. doi:10.2307/2118575. Artikkelin verkkoversio.
- ↑ Penrose Tiles Talk Across Miles American Mathematical Society. Viitattu 27.9.2018.
- ↑ Aperiodic Tiling University of London, EPSRC. Arkistoitu 29.8.2017. Viitattu 27.9.2018.
- ↑ Hao Wang: Proving theorems by pattern recognition—II. Bell Sytem Technical Journal, 1961, nro 40, s. 1–41. doi:10.1002/j.1538-7305.1961.tb03975.x.
- ↑ Hao Wang: Games, logic and computers. Scientific American, Marraskuu 1965, s. 98–106.
- ↑ Robert Berger: The undecidability of the domino problem. Memoirs of the American Mathematical Society, 1966, 66. vsk, nro 66. doi:10.1090/memo/0066.
- ↑ Raphael M. Robinson: Undecidability and nonperiodicity for tilings of the plane. Inventiones Mathematicae, 1971, 12. vsk, nro 2, s. 177–209. doi:10.1007/bf01418780.
- ↑ Karel II Culik: An aperiodic set of 13 Wang tiles. Discrete Mathematics, 1966, 160. vsk, nro 1–3, s. 245–251. doi:10.1016/S0012-365X(96)00118-5.
- ↑ Cameron Browne: Truchet curves and surfaces. Computer & Graphics, 2008, 32. vsk, nro 2, s. 268–281. doi:10.1016/j.cag.2007.10.001.
- ↑ The tiling patterns of Sebastian Truchet and the topology of structural hierarchy. Leonardo, 1987, 20. vsk, nro 4, s. 373–385. doi:10.2307/1578535.
- ↑ Michiel Hazewinkel (toim.): ”Four-colour problem”, Encyclopedia of Mathematics. Springer Science+Business Media B.V. / Kluwer Academic Publishers, 2001. ISBN 978-1-55608-010-4.
- ↑ a b Malcolm E. Lines: ”Aristoteleesta lasin rakenteeseen”, Jättiläisten harteilla: matematiikan heijastuksia luonnontieteisiin, s. 17–22. Suomentanut Veli-Pekka Ketola. Art House, 2000. ISBN 951-884-285-X.
- ↑ Pentagon Tiling Wolfram MathWorld. Eric W. Weisstein. Viitattu 21.9.2018.
- ↑ Franz Aurenhammer: Voronoi Diagrams – A Survey of a Fundamental Geometric Data Structure. ACM Computing Surveys, {{{Vuosi}}}, 23. vsk, nro 3, s. 345–405. doi:10.1145/116873.116880.
- ↑ Atsuyuki Okabe, Barry Boots, Kokichi Sugihara, Sung Nok Chiu: Spatial Tessellations – Concepts and Applications of Voronoi Diagrams (2. painos). John Wiley, 2000. ISBN 0-471-98635-6.
- ↑ Paul Louis George: Delaunay Triangulation and Meshing: Application to Finite Elements, s. 34–35. Hermes, 1991. ISBN 2-86601-692-0.
- ↑ Jesper Moller: Lectures on Random Voronoi Tessellations. Springer, 1994. ISBN 978-1-4612-2652-9. Teoksen verkkoversio.
- ↑ H. A. Schwarz: Ueber diejenigen Fälle in welchen die Gaussichen hypergeometrische Reihe eine algebraische Function ihres vierten Elementes darstellt. Journal für die reine und angewandte Mathematik, 1873, nro 75, s. 292–335. ISSN 0075-4102. doi:10.1515/crll.1873.75.292. Artikkelin verkkoversio.
- ↑ Schwarz Triangle Wolfram MathWorld. Eric W. Weissman. Viitattu 25.9.2018.
- ↑ a b c d Malcolm E. Lines: ”Aristoteleesta lasin rakenteeseen”, Jättiläisten harteilla: matematiikan heijastuksia luonnontieteisiin, s. 25. Suomentanut Veli-Pekka Ketola. Art House, 2000. ISBN 951-884-285-X.
- ↑ Pater Engel: Über Wirkungsbereichsteilungen von kubischer Symmetrie. Zeitschrift für Kristallographie, Kristallgeometrie, Kristallphysik, Kristallchemie, 1981, 154. vsk, nro 3–4, s. 199–215. doi:10.1524/zkri.1981.154.3-4.199.
- ↑ Branko Grünbaum: Uniform tilings of 3-space. Geombinatorics, 1994, 4. vsk, nro 2, s. 49–56.
- ↑ H. E. Hall: ”Typical Crystal Structures”, Solid state physics, s. 31–32. John Wiley & Sons Ltd., 1974. ISBN 0-471-34280-7.
- ↑ Malcolm E. Lines: ”Lattialaatoista kvasikiteisiin”, Jättiläisten harteilla: matematiikan heijastuksia luonnontieteisiin, s. 121–122. Suomentanut Veli-Pekka Ketola. Art House, 2000. ISBN 951-884-285-X.
- ↑ Philip Ball: ”Mahdoton järjestys: Kun atomit kohtaavat geometrian”, Kemian eturintamassa, s. 164–166. Suomentanut Kimmo Pietiläinen. Terra Cognita, 1997. ISBN 952-5202-07-0.
- ↑ Harold Scott Macdonald Coxeter, F. Arthur Sherk: Kaleidoscopes: Selected Writings of H.S.M. Coxeter. Canadian Mathematical Society; John iley & Sons, 1995. ISBN 978-0-471-01003-6. Teoksen verkkoversio.
- ↑ Marjorie Senechal: Quasicrystals and Geometry, s. 209. CUP Archive, 1996. ISBN 978-0-521-57541-6. Teoksen verkkoversio.
- ↑ Maurice Margenstern, Cornell University Library: Coordinates for a new triangular tiling of the hyperbolic space arxiv.org. Viitattu 27.9.2018.
- ↑ Tiling the Hyperbolic Plane with Regular Polygons demonstrations.wolfram.com. Viitattu 27.9.2018.
- ↑ H.S.M. Coxeter: ”Chapter 10: Regular honeycombs in hyperbolic spave”, The Beauty of Geometry: Twelve Essays, s. 212–213. Dover Publications, 1999. ISBN 0-486-40919-8.
- ↑ Mathematics in Art and Architecture National University of Singapore. Viitattu 27.9.2018.
- ↑ Andrew Whittaker: Speak the Culture: Spain Sivu = 153. Thorogood Publishing, 2008. ISBN 978-1-85418-605-8. Teoksen verkkoversio.
- ↑ J. L. Locher (toim.): The World of M. C. Escher, s. 5, 17. Abrams, 1974. ISBN 0-451-79961-5.
- ↑ Introduction to Hyperbolic and Automatic Groups University of Utah. Viitattu 27.9.2018.
- ↑ Hyperbolic Escher josleys.com. Viitattu 27.9.2018.
- ↑ J. L. Locher (toim.): The World of M. C. Escher, s. 142–143. Abrams, 1974. ISBN 0-451-79961-5.
- ↑ J. L. Locher (toim.): The World of M. C. Escher, s. 16. Abrams, 1974. ISBN 0-451-79961-5.
- ↑ Eric Gjerde: Origami Tessellations. Taylor and Francis, 2008. ISBN 978-1-568-81451-3.
- ↑ Reducing yield losses: using less metal to make the same thing UIT Cambridge. Arkistoitu 29.5.2015. Viitattu 27.9.2018.
- ↑ M. D. Thouless: Crack Spacing in Brittle Films on Elastic Substrates. J. Am. Chem. Soc., 1990, s. 2144–2146. doi:10.1111/j.1151-2916.1990.tb05290.x.
- ↑ Z. C. Xia, J. W. Hutchinson: Crack patterns in thin films. Journal of the Mechanics and Physics of Solids, 2000, 48. vsk, s. 1107–1131. doi:10.1016/S0022-5096(99)00081-2.
- ↑ Controlled mud-crack patterning and self-organized cracking of polydimethylsiloxane elastomer surfaces. Scientific Reports, 2015, nro 5. doi:10.1038/srep14787.
- ↑ How honeycombs can build themselves Nature.com. Viitattu 27.9.2018.
- ↑ Kirjopikarililja Luontoportti.com. Viitattu 27.9.2018.
- ↑ Colchicums: autumn's best-kept secret. American Gardener, syys-lokakuu 2007, s. 18–22.
- ↑ Limit theory for planar Gilbert tessellations arxiv.org. 30.4.2010. Cornell University Library. Viitattu 27.9.2018.
- ↑ B. Noble (toim.); Edgar Gilbert: ”Random plane networks and needle-shaped crystals”, Applications of Undergraduate Mathematics in Engineering. Macmillan, 1967.
- ↑ D. Weaire, N. Rivier: Soap, cells and statistics: Random patterns in two dimensions. Contemporary Physics, 1984, 25. vsk, nro 1, s. 59–99. doi:10.1080/00107518408210979.
- ↑ D. F. Branagan, G. C. Nanson: Tesselated pavements, s. 11–20. University of Wolongong. ISBN 0-864-18001-2.
- ↑ Philip Ball: Shapes, s. 73–76. Oxford University Press, 2009. ISBN 978-0-199-60486-9.
- ↑ History of Jigsaw Puzzles American Jigsaw Puzzle Society. Arkistoitu 19.10.2000. Viitattu 27.9.2018.
- ↑ Jerry Slocum: The Tao of Tangram, s. 9. Barnes & Noble, 2001. ISBN 978-1-4351-0156-2.
- ↑ Solomon W. Golomb: Polyominies. Princeton University Press, 1994. ISBN 0-691-02444-8.
- ↑ George E. Martin: Polyominoes: A guide to puzzles and problems in tiling. Mathematical Association of America, 1991.
- ↑ Greg N. Frederickson: Hinged Dissections: Swinging and Twisting. Cambridge University Press, 2002. ISBN 0521811929. Teoksen verkkoversio.
- ↑ Martin Gardner: On 'Rep-tiles,' Polygons that can make larger and smaller copies of themselves. Scientific American, Toukokuu 1963, nro 208, s. 154–164.
- ↑ Martin Gardner: Aha! A Two Volume Collection: Aha! Gotcha Aha! Insight, s. 48. MAA, 2006. ISBN 978-0-88385-551-5. Teoksen verkkoversio.
- ↑ The Importance of Recreational Math New York Times. Viitattu 27.9.2018.
- ↑ Doris Schattschneider: Tiling the Plane with Congruent Pentagons. Mathematics Magazine, 1978, 51. vsk, nro 1, s. 29–44. doi:10.2307/2689644.
- ↑ Squaring the Square Squaring.net. Viitattu 27.9.2018.
- ↑ Martin Gardner, William T. Tutte: Mathematical Games. Scientific American, Marraskuu 1958.
- ↑ Frederick V. Henle, James M. Henle: Squaring the plane. American Mathematical Monthly, 2008, nro 115, s. 3–12. Artikkelin verkkoversio.
Aiheesta muualla
[muokkaa | muokkaa wikitekstiä] Kuvia tai muita tiedostoja aiheesta Tessellaatio Wikimedia Commonsissa
Kuvia tai muita tiedostoja aiheesta Tessellaatio Wikimedia Commonsissa