Tasasivuinen kolmio
Wikipedia
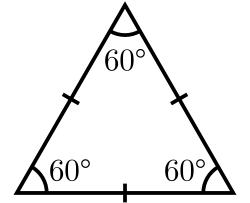
Tasasivuinen kolmio on kolmio, jonka kaikki sivut ovat yhtä pitkiä. Tasasivuisen kolmion kulmat ovat yhtä suuria, suuruudeltaan 60°.
Tasasivuisen kolmion korkeus saadaan kertomalla sen sivun pituus luvulla 
, joka on noin 0,866. Sen pinta-ala on yhtä suuri kuin sen sivun neliö kerrottuna luvulla 
, joka on noin 0,433.
Vivianin lauseen mukaan tasasivuisen kolmion sivujen etäisyydet kolmion sisällä olevasta pisteestä ovat yhteenlaskettuna sama kuin kolmion korkeus.
