Säännöllinen monikulmio

Säännöllinen monikulmio on geometriassa konveksi monikulmio, joka on samalla sekä syklinen monikulmio että tangentiaalinen monikulmio, ja jolla erityisesti kaikki sivut ovat yhtä pitkiä ja kaikki kulmat yhtä suuria. Säännöllinen monikulmio on siis tasasivuinen ja tasakulmainen. Säännöllisestä muodosta johtuen sillä on olemassa useita symmetria-akseleita ja keskipiste. Säännöllisten monikulmioiden avulla etsittiin antiikin aikana piille likiarvoja.

Säännöllisiä monikulmioita ovat esimerkiksi seuraavat monikulmiot:

• 

  Tasasivuinen kolmio

• 

  Neliö

• 

  Säännöllinen viisikulmio

• 

  Säännöllinen kuusikulmio

• 

  Säännöllinen seitsenkulmio

• 

  Säännöllinen kahdeksankulmio

• 

  Säännöllinen yhdeksänkulmio

• 

  Säännöllinen kymmenkulmio

Nimityksiä

Apoteema eli pikkusäde r_i, isosäde r_u, sivun pituus a, sisäkulma 120^o sekä keskuskulma 60^o ja sen keskuskolmio.

Monikulmioita nimitetään lukusanan avulla esimerkiksi viisikulmioksi. Yleistäen, jos monikulmiossa on n kulmaa, sitä voidaan kutsua n-kulmioksi. Tällaisella säännöllisellä monikulmiolla on siten n kulmaa, kärkeä ja sivua. Kaikki kulmat ovat määritelmän mukaan saman suuruisia, joten monikulmio on tasakulmainen, ja kaikki sivut ovat saman pituisia, joten se on myös tasasivuinen.

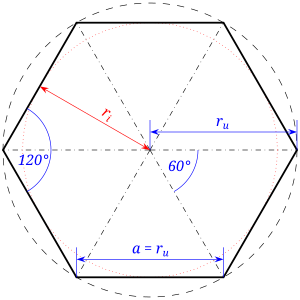
Säännöllinen monikulmio voidaan ajatella säännölliseksi sykliseksi monikulmioksi, jonka kärjet sijaitsevat ympyrän kehällä säännöllisin välein. Ympyrää kutsutaan monikulmion ympäri piirretyksi ympyräksi eli lyhyemmin ulkoympyräksi. Ulkoympyrän keskipiste on samalla monikulmion symmetriapiste, jota voidaan kutsua myös monikulmion keskipisteeksi. Monikulmion kärjet sijaitsevat ison säteen R etäisyydellä keskipisteestä ja säteillä voidaan jakaa monikulmio tasakylkisiin kolmioihin, joita on yhtä monta kuin sivujakin. Kolmioita nimitetään keskuskolmioiksi. Keskipisteen ja sivun välistä etäisyyttä kutsutaan apoteemaksi eli sisään piirretyn monikulmion sivun etäisyydeksi.

Säännöllinen monikulmio voidaan myös ajatella säännölliseksi tangentiaaliseksi monikulmioksi, jonka sivut sivuavat tangentteina monikulmion sisälle piirrettyä ympyrää. Tätä ympyrää voidaan kutsua monikulmion sisälle piirretyksi ympyräksi eli lyhyemmin sisäympyräksi. Sisäympyrän sädettä r kutsutaan pieneksi säteeksi ja sen arvo on sama kuin edellä mainitulla apoteemalla.

Ominaisuuksia

Säännölliset monikulmiot perivät kaikki yleisen monikulmion ominaisuudet. Niillä on säännöllisyydestä johtuen paljon erityisiä ominaisuuksia:

• Säännöllisen monikulmion ympäri ja sisälle voidaan aina piirtää edellä kuvatulla tavalla ympyrät.
• Jos annetaan kulmien lukumäärä ja piirin pituus, kaikista näin muodostetuista monikulmioista säännöllisellä monikulmiolla on suurin pinta-ala.
• Jos annetaan kulmien lukumäärä ja pinta-alan suuruus, kaikista näin muodostetuista monikulmioista säännöllisellä monikulmiolla on lyhin piiri.
• Jos säännöllisen monikulmion sisältä valitaan mielivaltaisesti sisäpiste, niin sisäpisteestä sivuille piirrettyjen kohtisuorien yhteispituus on sama kuin "apoteema kertaa n".

Seuraavissa kaavojen suureet tarkoittavat: s on sivun pituus, a on apoteema, p on piiri, A on ala, n on kulmien lukumäärä, $\alpha$ on sisäkulman suuruus.

Kulmat

• Sisäkulma on $\alpha ={\frac {n-2}{n}}\cdot 180^{\circ }$.
• Ulkokulma eli sivun ja viereisen sivun jatkeen välinen kulma $\beta ={\frac {360^{\circ }}{n}}$
• keskuskolmion keskuskulma β on yhtä suuri kuin ulkokulma: $\beta =\delta$

Sivunpituus

Sivun pituus voidaan määrittää trigonometristen funktioiden avulla.

Sivun pituus lasketaan: $s=2r\tan {\frac {180^{\circ }}{n}}=2R\sin {\frac {180^{\circ }}{n}}={\sqrt {\frac {4A\tan {\frac {180^{\circ }}{n}}}{n}}}$

Tietyillä kulmilla sivun pituus voidaan määrittää tarkastikin:

• tasasivuinen kolmio: $s=R{\sqrt {3}}=2r{\sqrt {3}}$
• neliö: $s=R{\sqrt {2}}=2r$
• säännöllinen kuusikulmio: $s=R={\frac {2r{\sqrt {3}}}{3}}$

Sisä- ja ulkoympyrän säde

Kummallekin ympyrälle on omat trigonometriset kaavansa:

• Sisäympyrän säde: $r={\tfrac {1}{2}}s\cot {\frac {180^{\circ }}{n}}=R\cos {\frac {180^{\circ }}{n}}$
• Ulkoympyrän säde: $R={\tfrac {1}{2}}s\csc {\frac {180^{\circ }}{n}}=r\sec {\frac {180^{\circ }}{n}}$

Koska trigonometriset funktiot antavat tarkkoja arvoja tietyillä kulmilla, voidaan säde ilmoittaa tarkastikin:

• tasasivuinen kolmio: $r={\frac {s{\sqrt {3}}}{6}}$ ja $R={\frac {s{\sqrt {3}}}{3}}$
• neliö: $r={\frac {s}{2}}$ ja $R={\frac {s{\sqrt {2}}}{2}}$
• säännöllinen viisikulmio: $r={\frac {s}{10}}{\sqrt {25+10{\sqrt {5}}}}$ ja $R={\frac {s}{10}}{\sqrt {50+10{\sqrt {5}}}}$
• säännöllinen kuusikulmio: $r={\frac {s{\sqrt {3}}}{2}}$ ja $R=s$

Pinta-ala

Pinta-ala voidaan ilmaista monella eri tavalla. Yksinkertainen geometrinen tapa on kertoa puolipiiri apoteemalla

$A={\frac {pa}{2}}={\frac {nsa}{2}}.$

Toisaalta se voidaan laskea trigonometriseti:

$A={\tfrac {1}{4}}ns^{2}\cot {\frac {180^{\circ }}{n}}=nr^{2}\tan {\frac {180^{\circ }}{n}}={\tfrac {1}{2}}nR^{2}\sin {\frac {360^{\circ }}{n}}$.

Koska trigonometriset funktiot antavat tarkkoja arvoja tietyillä kulmilla, voidaan pinta-ala ilmoittaa tarkastikin:

• tasasivuinen kolmio: $A={\frac {s^{2}{\sqrt {3}}}{4}}$
• neliö: $A=s^{2}$
• säännöllinen viisikulmio: $A={\frac {s^{2}}{4}}{\sqrt {25+10{\sqrt {5}}}}$
• säännöllinen kuusikulmio: $A={\frac {3s^{2}{\sqrt {3}}}{2}}$

Konstruktiot

Geometriassa on antiikin ajoista lähtien yritetty konstruoida säännöllisiä monikulmioita pelkästään harppia ja viivainta käyttämällä. Jo se kysymys, onko se ylipäätään mahdollista, on ollut vaikea kysymys vastattavaksi. Saksalainen Carl Gauss todisti, että sellaiset säännölliset n-kulmiot ovat konstruoitavissa, jossa $n=2^{p}$ (jossa $p\geq 2$), tai $n=2^{p}(2^{2^{k}}+1)$ (jossa $p\geq 0,\,k\geq 0,\,ja\,2^{2^{k}}+1$ on alkuluku). Ensimmäisen säännön mukaan konstruoitavia n-kulmioita ovat 4-, 8-, 16-, 32-, ... ja niin edelleen. Toisen säännön mukaan näiden lisäksi voidaan konstruoida vielä 3-, 6-, 12-, 24-, ... sekä 5-, 10-, 20-, 40-, ... sekä 17-, 34-, 68-, ... sekä 257- ja 65537-kulmioita ja niin edelleen.

Historiaa: Piin määritys

Arkhimedeen tapa laskea piin arvo käyttämällä säännöllisiä monikulmioita ympyrän sisä- ja ulkopuolella. Kun kulmien lukumäärää kasvatettiin, saatiin monikulmioiden piirin pituuksiksi arvoja, joiden välissä 2πr tuli olla.

N-kulmioiden kulmia lisättiin puolittamalla edellisen laskun monikulmion keskuskulmaa. Lähtien 4-kulmiosta liikkeelle jatkettiin 8-, 16-, 32- ja 64-kulmiolla. Samaa tehtiin tahdissa ympyrää ympäröivälle n-kulmiolle.

Antiikin suureen ajattelijaan Arkhimedeeseen on liitetty piin arvon laskeminen. Hän piirsi ympyrän ympärille ja sisäpuolelle n-kulmiot, joiden piirien pituudet hän laski. Ulkopuolen piirin pituus oli luonnollisesti pitempi kuin ympyrän kehä, ja sisäpuolisen n-kulmion piiri sitä pienempi. Piin likiarvoksi saatiin tällä menetelmällä piin ylä- ja alarajan keskiarvo. Kun kulmien lukumäärää n suurennettiin puolittamalla edellisen kuvion kulmia, tarkentui piin likiarvo. Piin määrittämiseksi on keskitty lukuisia muitakin menetelmiä, joten tällä menetelmällä on enää lähinnä historiallinen arvo.

Vertailutaulukko

$n$: Kulmaluku

$\varphi$: Sivua vastaava keskuskulma

$a$: Sivunpituus

$R$: Ulkoympyrän säde

$r$: Sisäympyrän säde

$\beta$: Sisäkulma

$A$: Pinta-ala

$n$	Nimitys	$\varphi$	${\frac {a}{R}}$	${\frac {r}{R}}$	$\beta$	${\frac {A}{R^{2}}}$	Kuvio
2	Jana	180°	2,0000	0,0000	0	0,0000
3	Kolmio	120°	1,7321	0,5000	60	1,2990
4	Nelikulmio	90°	1,4142	0,7071	90	2,0000
5	Viisikulmio	72°	1,1756	0,8090	108	2,3776
6	Kuusikulmio	60°	1,0000	0,8660	120	2,5981
7	Seitsemänkulmio	51,43°	0,8678	0,9010	128,57	2,7364
8	Kahdeksankulmio	45°	0,7654	0,9239	135	2,8284
9	Yhdeksänkulmio	40°	0,6840	0,9397	140	2,8925
10	Kymmenenkulmio	36°	0,6180	0,9511	144	2,9389
11	11-kulmio	32,73°	0,5635	0,9595	147,27	2,9735
12	12-kulmio	30°	0,5176	0,9659	150	3,0000
13	13-kulmio	27,69°	0,4786	0,9709	152,31	3,0207
14	14-kulmio	25,71°	0,4450	0,9749	154,29	3,0372
15	15-kulmio	24°	0,4158	0,9781	156	3,0505
16	16-kulmio	22,5°	0,3902	0,9808	157,5	3,0615
17	17-kulmio	21,18°	0,3675	0,9830	158,82	3,0706
18	18-kulmio	20°	0,3473	0,9848	160	3,0782
19	19-kulmio	18,95°	0,3292	0,9864	161,05	3,0846
20	20-kulmio	18°	0,3129	0,9877	162	3,0902
21	21-kulmio	17,14°	0,2981	0,9888	162,86	3,0949
22	22-kulmio	16,36°	0,2846	0,9898	163,64	3,0991
23	23-kulmio	15,65°	0,2723	0,9907	164,35	3,1027
24	24-kulmio	15°	0,2611	0,9914	165	3,1058
25	25-kulmio	14,4°	0,2507	0,9921	165,6	3,1086
26	26-kulmio	13,85°	0,2411	0,9927	166,15	3,1111
27	27-kulmio	13,33°	0,2322	0,9932	166,67	3,1133
28	28-kulmio	12,86°	0,2239	0,9937	167,14	3,1153
29	29-kulmio	12,41°	0,2162	0,9941	167,59	3,1171
30	30-kulmio	12°	0,2091	0,9945	168	3,1187

Lähteet

• Väisälä, Kalle: Geometria. Porvoo: Wsoy, 1959. Teoksen verkkoversio (pdf) (viitattu 29.9.2013).
• Yiu, P.: Euclidean Geometry (luentomoniste) http://math.fau.edu/yiu/Geometry.html. 1998. Florida Atlantic University. Viitattu 29.9.2013.

Aiheesta muualla

• G.H. Hughes: The Polygons of Albrecht Dürer -1525 arXiv.org. Viitattu 5.10.2013.