Tasakulmainen monikulmio
Tasakulmainen monikulmio on geometriassa monikulmio, joka kaikki kulmat ovat yhtä suuret.[1] Jos vielä sivutkin ovat yhtä pitkät, on kyseessä säännöllinen monikulmio.[2][3]
Tasakulmaiset monikulmiot perivät kaikki yleisen monikulmion ominaisuudet, mutta tasakulmaisuudesta seuraa esimerkiksi seuraava ominaisuus. Konveksin monikulmion kulmien summa saadaan määritettyä jakamalla monikulmio osakolmioihin. Niitä saadaan n-kulmiolle, jossa on n kappaletta kulmaa, aina n - 2 kappaletta. Jokaisen kolmion kulmien summa on 180°, joten n-kulmion kulmien summa on
Koska tasakulmaisessa n-kulmiossa kaikki kulmat ovat samoja, antaa tämä yhdelle sisäkulmalle
Esimerkkejä[muokkaa | muokkaa wikitekstiä]
Seuraavat esimerkit ovat konvekseja monikulmioita. Sallimalla sellaisia kulmia, jotka "kääntyvät sisäalueen ulkopuolelle", kasvaa variaatioiden lukumäärä suuresti.
Kolmio[muokkaa | muokkaa wikitekstiä]
Kolmiossa sisäkulmien summa on 180°. Jokaiselle kulmalle riittää siitä 60°. Johtuen kolmion yksinkertaisesta rakenteesta, on tämän muotoisia kolmioita vain yksi. Tasasivuinen kolmio on tasakulmaisena myös säännöllinen kolmio.[4]
-
Tasasivuinen kolmio
-
Suorakulmio
-
Neliö
Nelikulmio[muokkaa | muokkaa wikitekstiä]
Konveksissa nelikulmiossa sisäkulmien summa on 360° ja se jaettuna neljälle kulmalle antaa sisäkulmaksi 90°. Näitä kutsutaan suorakulmaisiksi nelikulmioiksi eli suorakulmioiksi, koska niillä on vain suoria kulmia. Sellainen suorakulmio, jonka sivut ovat saman pituisia, kutsutaan neliöksi ja se on siten säännöllinen nelikulmio.
Mielenkiintoinen poikkeus syntyy ajatuksesta, että yksi kulma olisi 270°. Silloin muidenkin kulmien olisi oltava sama 270° ja kuvioksi syntyy "nurinkurinen" suorakulmio.
Viisikulmio[muokkaa | muokkaa wikitekstiä]
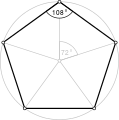
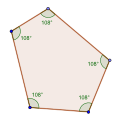
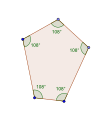
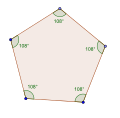
Konveksissa viisikulmiossa sisäkulmien summa on 540°, joka antaa kulmille 108°.
-
Säännöllinen viisikulmio
-
Tasakulmainen viisikulmio
Kuusikulmio[muokkaa | muokkaa wikitekstiä]
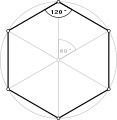
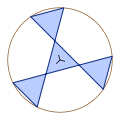
Konveksissa kuusikulmiossa sisäkulmien summa on 720°, joka antaa kulmille 120°.
-
Säännöllinen kuusikulmio
-
Itseään leikkaava tasakulmainen kuusikulmio.
Lähteet[muokkaa | muokkaa wikitekstiä]
Viitteet[muokkaa | muokkaa wikitekstiä]
- ↑ Weisstein, Eric W.: Equiangular Polygon (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)
- ↑ Weisstein, Eric W.: Equilateral Polygon (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)
- ↑ Weisstein, Eric W.: Regular Polygon (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)
- ↑ Weisstein, Eric W.: Equilateral Triangle (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)
Aiheesta muualla[muokkaa | muokkaa wikitekstiä]
- Cut-the_Knot: Equiangular Polynomy