Voronoin diagrammi

Voronoin diagrammi on matematiikassa tason jako osiin annetusta erillisten pisteiden joukosta mitattujen etäisyyksien perusteella. Tämä pistejoukko, johon kuuluvia pisteitä sanotaan siemeniksi, kohteiksi tai generaattoreiksi, oletetaan ennalta annetuksi, ja kutakin tällaista kohdetta vastaava alue käsittää ne alkuperäisen tasoalueen pisteet, jotka ovat lähempänä kyseistä kohdetta kuin mitään muuta. Näin muodostettuja alueita sanotaan Voronoin soluiksi. Pistejoukon määrittämä Voronoin diagrammi on sen Delaunayn kolmioinnin duaali.
Voronoin diagrammi on saanut nimensä Georgi Voronoin mukaan. Siitä käytetään myös nimityksiä Voronoin tessellaatio, Voronoin dekompositio, Voronoin partitio tai Dirichlet’n tessellaatio[1] (Peter Gustav Lejeune Dirichlet’n mukaan). Voronoin diagrammeilla on käytännöllisiä ja teoreettisia sovelluksia monilla aloilla, pääasiassa tieteessä ja teknologiassa mutta myös kuvataiteissa.[2][3] Alueita, joihin Voronoin diagrammi tason jakaa, sanotaan myös Thiessenin monikulmioiksi.[4][5]
Yksinkertaisin tapaus[muokkaa | muokkaa wikitekstiä]
Yksinkertaisimmassa tapauksessa, jota esittää edellä oleva kuva, on annettu äärellinen joukko euklidisen tason pisteitä: {p1, ..., pn}. Tässä tapauksessa jokainen kohde pk on vain yksi piste, ja sitä vastaava Voronoin solu Rk käsittää ne euklidisen tason pisteet, joiden etäisyys pisteestä pk on pienempi tai yhtä suuri kuin mistään muusta annettuun joukkoon kuuluvasta pisteestä. Jokainen sellainen solu voidaan muodostaa puolitasojen leikkauksena, ja näin ollen kaikki nämä solut ovat muodoltaan kuperia ja ovat joko monikulmioita tai ulottuvat äärettömän kauas. Voronoin diagrammin janat käsittävät kaikki ne tason pisteet, jotka ovat yhtä etäällä kahden lähimmästä kohteesta. Voronoin kärjet eli solmut ovat pisteet, jotka ovat yhtä etäällä kolmesta tai useammasta kohteesta.
Muodollinen määritelmä[muokkaa | muokkaa wikitekstiä]
Olkoon metrinen avaruus, jonka etäisyysfunktio on . Olkoon joukko indeksejä ja järjestetty joukko ei-tyhjiä osajoukkoja (kohteita) avaruudessa . Kohteeseen liittyvä Voronoin solu eli Voronoin alue, , on niiden :n pisteiden joukko, joiden etäisyys ei ole suurempi kuin niiden etäisyys muista kohteista , missä on mikä tahansa :sta poikkeava indeksin arvo. Toisin sanoen jos merkitsee pisteen ja osajoukon välistä etäisyyttä, on
Voronoin diagrammi on yksinkertaisesti solujen järjestetty joukko. Periaatteessa osa kohteista saattaa olla osittain tai jopa kokonaan päällekkäisiä (kuten jäljempänä olevassa sovelluksessa, jossa kohteet tarkoittavat kauppaliikkeitä), mutta tavallisesti niiden edellytetään olevan toisistaan erillisiä. LIsäksi määritelmä sallii, että kohteiden lukumäärä on ääretön, millä tapauksella on sovelluksia lukujen geometriassa ja kristallografiassa, mutta usein rajoitutaan tarkastelemaan tapauksia, joissa niiden lukumäärä on äärellinen.
Siinä erikoistapauksessa, että avaruus on äärellisulotteinen euklidinen avaruus, jokainen kohde pistemäinen, niiden lukumäärä äärellinen ja ne kaikki erillisiä, Voronoin solut ovat kuperia polytooppeja ja ne voidaan esittää kombinatorisella tavalla käyttämällä niiden kärkiä, tahkoja, kaksiulotteisia sivuja jne. Joskus indusoitua kombinatorista rakennetta sanotaan Voronnoin diagrammiksi. Yleisessä tapauksessa Voronoin solut eivät välttämättä ole kuperia tai edes yhtenäisiä.
Euklidisen avaruuden tapauksessa muodollinen määritelmä voidaan muotoilla uudestaan tavanomaisin termein. Jokainen Voronoin monitahokas liittyy generaattoripisteeseen . Olkoon euklidisen avaruuden kaikkien pisteiden joukko. Olkoon
- piste, joka generoi Voroinoin alueen ,
- piste, joka generoi alueen ,
- piste, joka generoi alueen ,
ja niin edelleen. Silloin jokainen Voronoin monikulmion piste on lähempänä tämän monikulmion generaattoripistettä kuin mitään muuta generaattoripistettä.[6]
Esimerkki[muokkaa | muokkaa wikitekstiä]
Yksinkertaisena sovellusesimerkkinä voidaan tarkastella jonkin alan liikkeiden sijaintia kaupungissa. Oletetaan, että on arvioitava asiakkaiden lukumäärä kussakin liikkeessä. Jos liikkeet ovat kaikissa muissa suhteissa samanlaiset, esimerkiksi hintojen, tavaravalikoimien ja palvelun laadun osalta, voidaan olettaa, että yleensä jokainen asiakas käy lähimmässä kaupassa. Tässä tapauksessa voidaan muodostaa Voronoin diagrammi, jonka kohteet ovat nämä kauppaliikkeet. Kuhunkin yksittäiseen liikkeeseen liittyvä Voronoin solu voidaan siis käsittää alueeksi, jonka asukkaat käyvät ostoksilla kyseisessä liikkeessä.
Kahden pisteen välinen etäisyys voidaan määritellä eri tavoin. Geometriassa käytetään tavallisesti euklidista etäisyyttä: joka vastaa paikkojen välistä etäisyyttä linnunteitse. Kaupungissa on kuitenkin usein mielekkäämpää käyttää katuja pitkin mitattuja etäisyyksiä. Jos kaupunki on rakennettu säännöllisen ruutukaavan mukaan ja kadut ovat koordinaattiakselien suuntaisia, tällöin saadaan niin sanottu Manhattan-metriikka, jossa kahden pisteen välinen etäisyys on :.[7] Voronoin diagrammit tulevat varsin eri näköisiksi riippuen siitä, kummalla tavalla etäisyydet määritellään eli kumpaa metriikkaa käytetään.
Ominaisuuksia[muokkaa | muokkaa wikitekstiä]
- Voronoin diagrammin Voronoin diagrammi euklidisessa avaruudessa, kun kohteet ovat pistemäisiä, on samojen pisteiden muodostama Delaunayn triangulaatio.
- Generoivista pisteistä kahta lähimpänä toista sijaitsevaa vastaavat Voronoin solut rajoittuvat toisiinsa.
- Jos euklidisella tasolla on annettuna joukko erillisiä pisteitä, kaksi pistettä ovat vielä
- Jos avaruus on normiavaruus ja etäisyys jokaisesta kohteesta on annettu (esimerkiksi jos kohteet ovat kompakteja joukkoja tai suljettuja palloja), jokainen Voronoin solu voidaan esittää kohteista eri suuntiin liittyvien janojen yhdisteenä.[8] Tämä ei välttämättä pidä paikkaansa, jos etäisyyttä ei ole annettu.
- Melko yleisillä ehdoilla (avaruus esimerkiksi voi olla ääretönulotteinen uniforminen kupera avaruus tai kohteita voi olla äärettömän monta) Voronoin solut ovat seuraavassa mielessä vakaita: jos kohteita siirretään jonkin matkaa tai niiden muotoa muutetaan jonkin verran, myös Voronoin soluihin tulee vain pieniä muutoksia.[9] Tämä ei kuitenkaan edes kaksiulotteisessa avaruudessa pidä kaikissa tapauksissa paikkansa, jos avaruus ei ole uniforminen ja kupera tai jos se ei ole euklidinen.
Historia ja tutkimus[muokkaa | muokkaa wikitekstiä]
Vähemmän muodollisesti Voronoin diagrammeja käsitteli jo Descartes vuonna 1644.[1]. Dirichlet käytti 2- ja 3-ulotteisia Voronoin diagrammeja apuna tutkiessaan neliömuotoja vuonna 1850.[1] Brittiläinen lääkäri John Snow käytti Voronoin diagrammia vuonna 1854 havainnollistamaan sitä, että useimmat koleraepidemian tuona vuonna Lontoossa tappamat ihmiset asuivat lähempänä tartunnan saanutta Broad Steetin pumppukaivoa kuin mitään muuta vesipumppua.
Nykyisen nimensä Voronoin diagrammit saivat venäläisen matemaatikon Georgi Voronoin mukaan, joka määritteli n-ulotteisen tapauksen ja tutki sitä vuonna 1908. Geofysiikassa ja meteorologiassa paikallisesti jakautuneen aineiston, esimerkiksi sademäärämittausten tuulosten analysointiin käytettyjä Voronoin diagrammeja sanotaan Thiessenin monikulmioiksi amerikkalaisen meteorologin Alfred H. Thiessenin mukaan. Tiiviin aineen fysiikassa vastaavanlalisia tessellaatioita sanotaan Wigner–Seitzin soluiksi. Kiteisen aineen käänteishilan Voronoin soluja sanotaan Brillouinin vyöhykkeiksi. Lien ryhmien yleisissä verkoissa soluja sanotaan yksinkertaisesti perusalueiksi. Yleisen metrisen avaruuden tapauksessa soluja sanotaan usein metrisiksi perusmonikulmioiksi.
Muita nimityksiä tälle käsitteelle tai joillekin sen tärkeille erikoistapauksille ovat: Voronoin monitahokkaat, Voronoin monikulmiot, vaikutusalue(et), Voronoin jako, Voronoin tessellaatio(t) ja Dirichlet'n tessellaatio(t).
Esimerkkejä[muokkaa | muokkaa wikitekstiä]

Kahdessa tai kolmessa ulottuvuudessa säännöllisten hilamaisten pistejoukkojen Voronoin tessellaatioita ovat monet tunnetut kuviot.
- kaksiulotteinen hila johtaa yleensä epäsäännölliseen hunajakennomaiseen tessellaatioon, jotka muodostuvat yhtä suurista pisteen suhteen symmetrisistä kuusikulmioista. Jos pisteet muodostavat säännöllisen kolmioverkon, Voronoin diagrammi on myös säännöllinen. Jos pisteet muodostavat suorakulmaisen hilan, kuusikulmioiden sijasta Voronoin solut ovat suorakulmioita tai erikoistapauksessa neliöitä. On kuitenkin myös muita pistejoukkoja, joiden generoima Voronoin diagrammi on suorakulmainen ruudokko; esimerkiksi vektorien (1,0) ja (1/2,1/2) määrittämän hilan Voronoin diagrammi on neliöruudukko.
- Yksinkertaisen kuutiollisen hilan Voronoin diagrammit ovat kuutioita.
- Heksagonaalisen tiivispakkauksen Voronoin solut ovat trapetsorombidodekaedreja.
- Pintakeskisen kuutiollisen hilan Voronoin solut ovat rombidodekaedreja.
- Tilakeskisen kuutiollisen hilan Voronoin solut ovat katkaistuja oktaedreja.
Pistejoukolle (x, y), missä x kuuluu diskreettiin joukkoon X ja y diskreettiin joukkoon Y, saadaan Voronoin diagrammiksi laatat, joissa nämä pisteet eivät välttämättä ole keskipisteinä.
Korkeamman kertaluvun Voronoin diagrammit[muokkaa | muokkaa wikitekstiä]
Normaali Voronoin solu määritellään niiden pisteiden joukoksi, jotka ovat lähempänä jotakin joukon S pistettä kuin mitään muuta saman joukon pistettä. Vastaavasti n:nnen kertaluvun Voronoin solu määritellään niiden pisteiden joukoksi, joihin liittyy n kappaletta joukon S pisteitä siten, että nämä pisteet ovat n lähimpänä sijaistevaa tämän joukon pistettä. Myös korkeamman kertaluvun Voronoin solut täyttävät yhdessä koko tason.
Korkeamman kertaluvun Voronoin diagrammit voidaan generoida rekursiivisesti. Jos (n - 1):nnen kertaluvun diagrammi tunnetaan, voidaan n:nnen kertaluvun diagrammi muodostaa korvaamalla jokainen joukon X = {x1, x2, ..., xn-1} generoima solu joukon S - X generoimalla Voronoin diagrammilla.
Kaukaisimpien pisteiden Voronoin diagrammi[muokkaa | muokkaa wikitekstiä]
Annetun n pisteen joukon (n - 1):nnen kertaluvun Voronoin diagrammia sanotaan kaukaisimpien pisteiden Voronoin diagrammiksi.
Jos on annettu pistejoukko S = {p1, p2, ..., pn}, kaukaisimpien pisteiden Voronoin diagrammi jakaa tason soluihin, joista kunkin muodostaa se tason alue, josta katsottuna jokin piste pi on kauempana kuin mikään muu joukon S piste. Jokaiseen tällaiseen kohteeseen ei välttämättä liity tällaista solua. Kohteeseen pi nimittäin liittyy tällainen solu, jos ja vain jos se on jokin suppeimman sellaisen kuperan monikulmion kärkipisteistä, johon kaikki S:n pisteet kuuluvat.
Olkoot H = {h1, h2, ..., hk} tämän kuperan monikulmion P kärkipisteiden joukko. Silloin kaukaisimpien pisteiden Voronoin diagrammi on tason jako k soluun, jollainen liittyy kuhunkin H:n pisteeseen siten, ett' piste q on kohteeseen hi liittyvässä solussa, jos ja vain jos d(q, hi) > d(q, pj) kaikilla pj ? S, joille hi ? pj, missä d(p, q) on pisteiden p ja q välinen euklidinen etäisyys.[10][11]
Kaukaisimpien pisteiden Voronoin diagrammin solujen välisillä rajoilla on topologisen reaalipuun rakenne äärettömät säteet lehtinään. Jokainen äärellinen puu on isomorfinen jonkin sellaisen puun kanssa, joka voidaan täten muodostaa kaukaisimpien pisteiden Voronoin diagrammista.[12]
Yleistyksiä ja muunnelmia[muokkaa | muokkaa wikitekstiä]
Kuten määritelmästäkin voi päätellä, Voronoin solut voidaan vastaavalla tavalla määritellä muissakin kuin euklidisessa metriikassa, esimerkiksi Mahalanobisin ja Manhattan-metriikassa. Näissä tapauksissa Voronoin solujen rajat voivat kuitenkin olla monimutkaisempia kuin euklidisessa tapauksessa.

Painotettu Voronoin diagrammi saadaan, kun suoraviivaiset etäisyydet generaattoripisteistä korvataan näiden etäisyyksien funktioilla, jotka saadaan antamalla kullekin generaattoripisteelle painokerroin, jolla etäisyys kerrotaan tai joka lisätään siihen. Kukin piste kuuluu siihen Voronoin soluun, jota vastaava näin määritelty funktio saa siinä pienimmän arvon. Toisin kuin metrisissä avaruuksissa, tässä tapauksessa osa Voronoin soluista saattaa olla tyhjiä joukkoja. Potenssidiagrammi on Voronoin diagrammi, jonka määritellään ympyräjoukon avulla käyttämällä etäisyyden mittana pisteen potenssia ympyröiden suhteen; se voidaan käsittää painotetuksi Voronoin diagrammiksi, jossa kunkin ympyrän sädettä käytetään painokertoimena ja lisätään ympyrän keskipisteestä mitatun etäisyyden neliöön.[13]
Useammassa kuin kahdessa ulottuvuudessa Voronoin diagrammit yleensä sangen monimutkaisia eivätkä ne usein edes ole käytännössä toteutettavissa. Vaihtoehtona on käyttää likimääräisiä Voronoin diagrammeja, joissa Voronoin solujen väliset rajat ovat sumeita ja voidaan toteuttaa likimääräisesti.[14]
Voronoin diagrammit liittyvät läheisesti muihin geometrisiin struktuureihin kuten esimerkiksi mediaaliakseliin, jolla on tietoteknisiä sovelluksia muun muassa kuvien segmentoinnissa, tekstintunnistuksessa, sekä vyöhykediagrammeihin. Ne eroavat Voronoin diagrammista siinä, että lähtökohtana olevat kohteet eli generaattorit eivät välttämättä ole pisteitä vaan voivat olla myös janoja tai monikulmioita. Lisäämällä diagrammiin janat, jotka yhdistävät näiden kohteiden lähimmät pisteet toisiinsa, tasoalue voidaan jakaa osiin.[15] Tätä struktuuria voidaan käyttää navigaatioverkkona kulkureitin löytämiseksi laajan alueen läpi. Navigaatioverkon käsitettä voidaan yleistää niin, että sitä voidaan soveltaa kolmiulotteisiin ympäristöihin kuten lentokenttään tai monikerroksisiin rakennuksiin.[16]
Sovelluksia[muokkaa | muokkaa wikitekstiä]
Luonnontieteissä[muokkaa | muokkaa wikitekstiä]

- Biologiassa Voronoin diagrammeja käytetään monien biologisten struktuurien kuten solujen[17] sekä luiden mikrorakenteen mallintamiseen.[18] Itse asiassa Voronoin tessellaatioita voidaan käyttää geometrisena apuvälineenä niiden fyysisten rajoitusten ymmärtämiseen, jotka ohjaavat kudosten muodostumista.[19]
- Hydrologiassa Voronoin diagrammeja käytetään alueellisten sademäärien laskemiseen, kun paikalliset sademäärät on mitattu erillisillä havaintopaikoilla. Tässä yhteydessä niitä kutsutaan tavallisesti Thiessenin monikulmioiksi.
- Ekologiassa Voronoin diagrammeja käytetään metsän kasvun tutkimiseen, ja niitä voidaan mahdollisesti soveltaa myös laadittaessa ennustemalleja metsäpaloille.
- Laskennallisessa kemiassa molekyylissä olevien atomiydinten mukaan määräytyviä Voronoin soluja käytetään atomien osittaisvarausten laskemiseen. Tämä suoritetaan Voronoin deformaatiotiheysmenetelmällä.
| Tämä artikkeli tai sen osa on tuotu vieraskielisestä lähteestä ja käännös on keskeneräinen. Voit auttaa Wikipediaa tekemällä käännöksen loppuun. |
Lääketieteessä[muokkaa | muokkaa wikitekstiä]
- Lääketieteellisessä diagnoosissa Voronoin diagrammeihin perustuvia lihaskudoksen malleja voidaan käyttää neuromuskulaaristen sairauksien toteamiseen.[19]
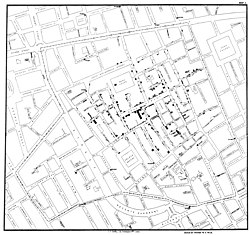
John Snow'n alkuperäinen diagrammi - Epidemiologiassa Voronoin diagrammeja voidaan käyttää tartunnan lähteiden jäljittämiseen epidemioiden esiintyessä. Yhtenä ensimmäisistä tällaisen tutkimuksen teki John Snow vuoden 1854 koleraepidemiasta Lontoon Sohossa. Hän osoitti tällä tavoin korrelaation koleratartunnan ja henkilön asuinpaikan välillä, mikä viittasi siihen, että valtaosa tartunnan saaneista ja siihen kuolleista oli saanut juomavetensä eräästä tietystä kaivosta.[20]
Insinöörialoilla[muokkaa | muokkaa wikitekstiä]
- Polymeerifysiikassa Voronoin diagrammeja voidaan käyttää esittämään polymeerien vapaata tilavuutta.
- Materiaalitieteissä metalliseosten monikiteistä mikrorakennetta kuvataan usein Voronoin diagrammeilla. Kiinteän olomuodon fysiikassa Wigner–Seitzin solut ovat kiteisen aineen Voronoin soluja. Kiteisiin, joiden symmetriaa esittää jokin avaruusryhmä, liittyy aaltovektoreiden muodostama käänteishila, jonka Voronoin soluja ovat Brillouinin vyöhykkeet.
- Ilmailussa valtamerikarttojen päälle asetetaan Voronoin diagrammit, jotka hätätilanteiden varalta osoittavat, mikä lentokenttä tai varalaskupaikka on lähimpänä lentoreitin kutakin kohtaa.
- Arkkitehtuurisa Voronoin mallit ovat muun muassa olleet perustana voittaneelle ehdotukselle Australian Gold Coastin taidekeskuksen, Home of the Artsin kehittämiseksi.[21]
- Kaupunkisuunnittelussa Voronoin diagrammeja voidaan soveltaa kaupungin sisäisten tavarankuljetusten kulkureittien optimointiin.[22]
- Kaivosalalla Voronoin monikulmioita käytetään arvokkaiden mineraalien ja muiden luonnonvarojen varantojen arviointiin. Tällöin paikkoja, joista tutkittavaa ainetta on löydetty, käytetään lähtökohtana Voronoin monikulmioiden muodostamiseen.
Geometriassa[muokkaa | muokkaa wikitekstiä]
- Pisteiden sijaintia esittävä tietorakenne voidaan rakentaa Voronoin diagrammin huipulle, jotta sen avulla voidaan vastata lähintä naapuria koskeviin kyselyihin sen selvittämiseksi, mikä tietynlaisista kohteista on lähimpänä annettua kohtaa. Lähimmän naapurein kyselyillä on useita sovelluksia. Niillä voidaan esimerkiksi selvittää, mikä sairaala sijaitsee lähimpänä tiettyä paikkaa, tai mikä kohteet tietokannassa ovat eniten toistensa kaltaisia. Laaja sovellusalue on vektorikvantisointi, jota paljon käytetään tiedonpakkauksessa.
- Geometriassa Voronoin diagrammeja voidaan käyttää löytämään pistejoukkoon liittyvä suurin tyhjä ympyrä ja sitä ympäröivä monikulmio. Tätä voidaan soveltaa esimerkiksi etsittäessä uudelle tavaratalolle kaupunkialueelta sijaintipaikka, jossa se on mahdollisimman kaukana kaikista aikaisemmista.
- Voronoin diagrammia yhdessä kaukaisimman pisteen Voronoin diagrammin kanssa käytetään tehokkaissa algoritmeissa, joilla lasketaan pistejoukon pyöreys.[10] Voroin lähestymistapa on käyttökelpoinen myös arvoitaessa pyöreyttä, kun tietoa haetaan koordinaattimittauskoneesta.
, niin että niitä voidaan käyttää verkon generointiin, pisteiden sijainnin selvittämiseen,
Tietojenkäsittelyssä[muokkaa | muokkaa wikitekstiä]
- Tietoverkkojen suunnittelussa Voronoin diagrammeja voidaan käyttää langattoman verkon kapasiteetin arviointiin.
- Tietokonegrafiikassa Voronoin diagrammeja käytetään muodostamaan kappaleen särkymistä tai murtumista esittävien mallien geometriseen muotoiluun. Niillä voidaan myös proseduraalisesti generoida kuvioita, jotka jäljittelevät elävien olentojen rakennetta.
- Automaattisessa robottinavigaatiossa Voronoin diagrammeja käytetään vapaiden kulkureittien löytämiseen. Jos pisteet merkitsevät esteitä, graafin kärjet vastaavat reittejä, jotka ovat kauimpana kaikista esteistä ja joissa törmäyksen vaara on pienin.
Paikallishallinnossa[muokkaa | muokkaa wikitekstiä]
Australian Victoriassa valtion koulut yleensä ottavat oppilaat siihen alkeis- tai ylemmän asteen kouluun, joka on lähimpänä kunkin oppilaan asuinpaikkaa.[23] Oppilaat ja heidän vanhempansa voivat nähdä tarkoitusta varten laaditun verkkosovelluksen avulla, mikä on lähin koulu.[24] Sovelluksessa paikallisen kartan päälle on asetettu Voronoin diagrammi, jonka kohteina ovat koulut.
Algoritmit[muokkaa | muokkaa wikitekstiä]
Nykyaikainen laskennallinen geometria on tuottanut tehokkaita algoritmeja Voronoin diagrammien muodostamiseksi.
Suoria algoritmeja ovat:
- Fortunen algoritmi on O(n log(n)) -algoritmi Voronoin diagrammin laatimiseksi annetusta tason pistejoukosta.
- Lloydin algoritmi ja sen yleistykset Linde-Buzo-Grayn algoritmin avulla käyttävät Voronoin tessellaatiota mielivaltaisen moniulotteisessa avaruudessa siten, että ne iteratiivisesti suppenevat kohti erästä Voronoin diagramin erityistä muotoa, jota sanotaan sentroidiseksi Voronoin tessellaatioksi. Siinä jokainen kohde on samalla solunsa keskipiste.
Bowyerin–Watsonin algoritmi, joka suoritusajaltaan vaihtelee O(n log(n)):sta O(n log(n2)):een. Se muodostaa ensin Delaunayn kolmioinnin missä tahansa määrässä ulottuvuuksia, minkä jälkeen sen avulla voidaan muodostaa Voronoin diagrammi.
Katso myös[muokkaa | muokkaa wikitekstiä]
Lähteet[muokkaa | muokkaa wikitekstiä]
- G. Lejeune Dirichlet: Über die Reduktion der positiven quadratischen Formen mit drei unbestimmten ganzen Zahlen. Journal für die Reine und Angewandte Mathematik, 1850, nro 40, s. 209–227. doi:10.1515/crll.1850.40.209.
- Georgy Voronoi: Nouvelles applications des paramètres continus à la théorie des formes quadratiques. Journal für die Reine und Angewandte Mathematik, 1908, nro 133, s. 97–178. doi:10.1515/crll.1908.133.97.
- Atsuyuki Okabe, Barry Boots, Kokichi Sugihara, Sung Nok Chiu: Spatial Tessellations – Concepts and Applications of Voronoi Diagrams (2nd edition. John Wiley, 2000. ISBN 0-471-98635-6.
- Franz Aurenhammer, Rolf Klein, Der-Tsai Lee: Voronoi Diagrams and Delaunay Triangulations. World Scientific, 2013. ISBN 978-9814447638.
- Adrian Bowuer: Computing Dirichlet tessellations. The Computer Journal, 1981, nro 2, s. 162–166. doi:10.1093/comjnl/24.2.162.
- Daniel Reem: An algorithm for computing Voronoi diagrams of general generators in general normed spaces. Proceedings of the sixth International Symposium on Voronoi Diagrams in science and engineering (ISVD 2009), 2009, s. 144–152. doi:10.1109/ISVD.2009.23.
- David F. Watson: Computing the n-dimensional Delaunay tessellation with application to Voronoi polytopes. The Computer Journal, 1981, nro 2, s. 167–172. doi:10.1093/comjnl/24.2.167.
- Mark de Berg, Marc van Kreveld, Mark OVermars, Otfried Schwarzkopf, Mark Overmars: ”Chapter 7: Voronoi Diagrams”, Computational Geometry, s. 147–163. Sisältää kuvauksen Fortunen algoritmista. Springer Verlag, 2000. ISBN 978-3-540-65620-3.
- Rolf Klein: Abstract voronoi diagrams and their applications. Computer Science: Lecture Notes in Computer Science, 1989, nro 333, s. 148–157. ISBN 978-3-540-52055-9. doi:10.1007/3-540-50335-8_31.
Viitteet[muokkaa | muokkaa wikitekstiä]
- ↑ a b c Voronoi Diagram Eric Weisstein. Viitattu 6.6.2019.
- ↑ Franz Aurenhammer: title=Voronoi Diagrams – A Survey of a Fundamental Geometric Data Structure. ACM Computing Surveys, 1991, s. 345–405. doi:10.1145/116873.116880.
- ↑ Atsuyiki Okabe, Barry Boots, Kokichi Sugihara, Sung Nok Chiu: Spatial Tessellations – Concepts and Applications of Voronoi Diagrams. 2. painos. John Wiley, 2000. ISBN 978-0-471-98635-5.
- ↑ Peter A. Burrough, Rachael McDonnell, Christopher D. Lloyd: ”Local, deterministic methods for interpolation”, Principles of Geographical Information Systems, s. 160. Oxford University Press, 1998. 978-0-19-874284-5. Teoksen verkkoversio.
- ↑ Zekai Sen: ”Delaney, Varoni, and Thiessen Polygons”, Spatial Modeling Priciples in Earth Sciences, s. 57. Springer, 2009. ISBN 978-3-319-41758-5. Teoksen verkkoversio.
- ↑ Q. T. Tran, D. Tainar, M. Safar: Transactions on Large-Scale Data- and Konwledge-Centered Systems, s. 357. {{{Julkaisija}}}, 2009. ISBN 9783642037214.
- ↑ Taxicab Metric MathWorld. Eric Weisstein. Viitattu 6.6.2019.
- ↑ Daniel Reem: An algorithm for computing Voronoi diagrams of general generators in general normed spaces. Proceedings of the Sixth International Symposium on Voronoi Diagrams in Science and Engineering (ISVD 2009), Vuosi = 2009, {{{Vuosi}}}, s. 144–152. ISBN 978-1-4244-4769-5.
- ↑ Daniel Reem: The geometric stability of Voronoi diagrams with respect to small changes of the sites. Proceedings of the 27th Annual SCM symposium on Compotational Geometry (SoCG, {{{Vuosi}}}, s. 254–263. doi:10.1145/1998196.1998234.
- ↑ a b Mark de Berg, Marc van Kreveld, Mark Overmars, Otfried Schwarzkoph: ”Luku 7.4: Farthest-Point Voronoi Diagrams”, Computational Geometry. Springer-Verlag, 2008. ISBN 978-3-540-77974-2.
- ↑ Sven Skyum: A simple algorithm for computing the smallest enclosing circle. Information Processing Letters, 18.2.1991, nro 3, s. 121–125. doi:10.1016/0020-0190(91)90030-L.
- ↑ Therese Biedl, Carsten Grimm Leonidas Palios, Jonathan Shewchuk, Sander Verdonschot: ”Realizing farthest-point Voronoi diagrams”, Proceedings of the 28th Canadian Conference on Computational Geometry (CCCG 2016). {{{Julkaisija}}}, 2016.
- ↑ Herbert Edelsbrunner: Algorithms in Combinatorial Geometry, contribution 13.6: Power Diagrams. EATCS Monographs on Theoretial Computer Science, 1987, s. 327–328. Springer Verlag.
- ↑ S. Arya, T. Malamatos, D. M. Mount: ”Space-Efficient Approximate Voronoi Diagrams”, Proc. 34th ACM Symp. on Theory of Computing (STOC 2002), s. 721–730. STOC, 2002. Teoksen verkkoversio.
- ↑ Roland Geraerts: ”Planning Short Paths with Clearance using Explicit Corridors”, Internationa Conference on Robotics and Automation, s. 1997–2004. IEEE, 2010. Teoksen verkkoversio. .
- ↑ Wouter G. van Toll, Atlas F. Cook IV, Roland Geraerts: ”Navigation Meshes for Realistic Multi-Layered Environments”, International Conference on Intelligent Robots and Systems, s. 3526–3532. IEEE/RSG, 2011. Teoksen verkkoversio.
- ↑ Martin Bock, Amit Kumar Tyagi, Jan Ulrich Kreft, Wolfgang Alt: Generalized Voronoi Tessellation as a Model of Two-dimensional Cell Tissue Dynamics. Bulletin of Mathematical Biology, 2009, nro 7, s. 1696–1731.
- ↑ Hui Li: Spatial Modeling of Bone Microarchitecture, 2012}}
- ↑ a b D. Sanchez-Gutierrez, M. Tozluoglu, J. D. Barry, A. Pascual, Y. Mao, L. M. Escudero: Fundamental physical cellular constraints drive self-organization of tissues. The EMBO Journal, {{{Vuosi}}}, nro 1, s. 77–88. doi:10.15252/embj.201592374. Artikkelin verkkoversio.
- ↑ Steven Johnson: The Ghost Map: The Story of London's Most Terrifying Epidemic — and How It Changed Science, Cities, and the Modern World, s. 187. Penguin Publishing Group, 2006. ISBN 978-1-101-15853-1. Teoksen verkkoversio.
- ↑ Gold Coast Cultural Precint: Hota Gallery ARM Architecture. Viitattu 6.6.2019.
- ↑ C. Lopez, C.-L. Zhao, S. Magniol, N. Chiabaut, L. Léclerc: Sustainability, 28.2.2019, nro 5. Artikkelin verkkoversio.
- ↑ Restrictions and boundaries www.education.vic.gov.au. Arkistoitu 31.5.2018. Viitattu 6.6.2019. (englanniksi)
- ↑ Melbourne School Zones melbourneschoolzones.com. Viitattu 6.6.2019.
Aiheesta muualla[muokkaa | muokkaa wikitekstiä]
 Kuvia tai muita tiedostoja aiheesta Voronoin diagrammi Wikimedia Commonsissa
Kuvia tai muita tiedostoja aiheesta Voronoin diagrammi Wikimedia Commonsissa






















![{\displaystyle \ell _{2}=d\left[\left(a_{1},a_{2}\right),\left(b_{1},b_{2}\right)\right]={\sqrt {\left(a_{1}-b_{1}\right)^{2}+\left(a_{2}-b_{2}\right)^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4dbecd722552090b30fcd0166107f3a2cece7e8d)
![{\displaystyle d\left[\left(a_{1},a_{2}\right),\left(b_{1},b_{2}\right)\right]=\left|a_{1}-b_{1}\right|+\left|a_{2}-b_{2}\right|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9da43d1f11cfcb755e4600f943fe4c8dedd46263)




