Ristitulo
Ristitulo eli vektoritulo on kolmiulotteisessa euklidisessa avaruudessa määritelty kahden vektorin välinen laskutoimitus, jonka merkkinä käytetään vinoristiä ×. Jos a ja b ovat kaksi erisuuntaista vektoria, niiden ristitulo a × b on vektori, joka on molempia vastaan kohtisuorassa ja näin ollen kohtisuorassa niiden määrittämään tasoon nähden. Ristitulolla on monia sovelluksia matematiikassa, fysiikassa, tekniikassa ja tietokoneohjelmoinnissa. Se on erotettava vektorien pistetulosta eli skalaaritulosta.
Jos vektorit ovat saman- tai vastakkaissuuntaisia, toisin sanoen ne eivät ole lineaarisesti riippumattomia, tai jompikumpi niistä on nollavektori, ristitulo on nollavektori. Muussa tapauksessa vektorien ristitulo on itseisarvoltaan (eli pituudeltaan) yhtä suuri kuin sen suunnikkaan pinta-ala, jonka sivuina nämä vektorit ovat; erityisesti toistensa nähden kohtisuorien vektorien ristitulo on niiden pituuksien tulo. Ristitulo on antikommutatiivinen, toisin sanoen a × b = -b × a), ja se noudattaa osittelulakia vektorien yhteenlaskun suhteen, toisin sanoen a × (b + c) = a × b + a × c). Avaruus varustettuna ristitulolla on algebra reaalilukujen kunnan yli. Se ei ole vaihdannainen eikä liitännäinen, mutta se on Lien algebra.
Pistetulon tavoin ristitulo riippuu euklidisen avaruuden metriikasta, mutta toisin kuin pistetulo, se riippuu myös avaruuden orientaatiosta eli kätisyydestä. Ristitulon käsitettä voidaan yleistää monin tavoin; se voidaan tehdä kätisyydestä riippumattomaksi tulkitsemalla tulos pseudovektoriksi, tai kuinka monessa ulottuvuudessa tahansa voidaan vektorien ulkoista tuloa käyttää niin, että tuloksena on bivektori tai 2-muoto. Käyttämällä orientaatiota ja metristä struktuuria aivan samoin kuin tavanomaisessa kolmiulotteisessa ristitulossa voidaan n ulottuvuudessa muodostaa n - 1 vektorin tulo niin, että se on kohtisuorassa niitä kaikkia vastaan. Kuitenkin vain kolmessa tai seitsemässä ulottuvuudessa [1] voidaan kahden vektorin ei-triviaali tulo määritellä niin, että tuloksena on vektori. Niistäkin vain kolmiulotteisessa avaruudessa ristitulo on yksikäsitteinen.

Määritelmä[muokkaa | muokkaa wikitekstiä]

Vektorien a ja b ristitulo on määritelty vain kolmiulotteisessa avaruudessa, ja se merkitään a × b. Fysiikassa käytetään joskus myös merkintää ,[2] mutta matematiikassa sitä vältetään käyttämästä, jottei se sekaantuisi ulkoiseen tuloon.
Ristitulo a × b määritellään vektorina c, joka on kohtisuorassa sekä a:ta että b:tä vastaan ja jonka suunta määräytyy oikean käden säännön mukaan ja joka pituudeltaan on yhtä suuri kuin sen suunnikkaan pinta-ala, jonka sivuina annetut vektorit ovat.
Ristitulo määritellään tällöin kaavalla [3][4]
missä on vektorien a ja b välinen kulma niiden määrittämässä tasossa (näin ollen se on aina 0°:n ja 180°:n välillä), ja ovat vektorien a ja b pituudet ja n niiden määrittämää tasoa vastaan kohtisuorassa oleva yksikkövektori, jonka suunta määräytyy oikean käden säännön mukaan oheisen kuvan osoittamalla tavalla. Jos vektorit a ja b ovat saman- tai vastakkaissuuntaisia ( eli niiden välinen kulma on joko 0° tai 180°), seuraa määritelmästä, että niiden ristitulo on nollavektori 0.

Sopimuksen mukaan vektorin n suunnan antaa oikean käden sääntö: jos oikean käden etusormi osoittaa vektorin a ja keskisormi vektorin b suuntaan, peukalo osoittaa vektorin n suuntaan oheisen kuvan mukaisesti. Tästä säännöstä seuraa, että ristitulo on antikommutatiivinen. Toisin sanoen, jos vektorit a ja b vaihdetaan keskenään, ristitulon suunta muuttuu vastakkaiseksi eli b × a = -(a × b). Niinpä jos oikean käden asentoa muutetaan siten, että etusormi osoittaa vektorin b ja keskisormi vektorin a suuntaan, osoittaa peukalo väistämättä päinvastaiseen suuntaan kuin aikaisemmin.
Edellä esitetystä määritelmästä seuraa, että ristituloa käytettäessä koordinaatiston kätisyys on otettava huomioon. Jos poikkeuksellisesti käytetään vasenkätistä koordinaatistoa, vektorin n suunnan antaa vasemman käden sääntö ja se osoittaa päinvastaiseen suuntaan.
Tästä aiheutuu kuitenkin ongelma, sillä jos yksi mielivaltainen vertailujärjestelmä vaihdetaan toiseen, esimerkiksi peilauksessa, jolloin siirrytään oikeakätisestä vasenkätiseen koordinaattijärjestelmään, ristitulon n suunta muuttuu. Tämän ongelma selviää, kun ymmärretään, ettei kahden vektorin ristitulo ole aito vektori vaan pseudovektori, kuten jäljempänä tarkemmin selitetään.
Nimet[muokkaa | muokkaa wikitekstiä]

Vuonna 1881 Josiah Willard Gibbs ja hänestä riippumatta Oliver Heaviside, ottivat käyttöön sekä pistetulon että ristitulon käyttämällä edellisen merkkeinä pistettä, (a . b), jälkimmäisen merkkinä vinoristiä ("x") (a x b).[5]
Vastaavia laskutoimituksia oli jo vuonna 1877 käyttänyt William Kingdon Clifford. Korostaakseen sitä, että toinen niistä antaa tuloksena skalaarin, toinen vektorin, hän antoi niille nimet skalaaritulo ja vektoritulo[5], joita edelleenkin yleisesti käytetään nimitysten pistetulo ja ristitulo ohella.
Siihen, että vektoritulon merkiksi valittiin vinoristi (a × b) ja sitä alettiin nimittää ristituloksi, vaikutti todennäköisesti se, että ristitulon a × b jokaista skalaarista komponenttia laskettaessa kerrotaan keskenään a:n ja b:n ne komponentit, jotka eivät vastaa toisiaan. Sitä vastoin pistetuloa a · b laskettaessa kerrotaan vektorien toisiaan vastaavat, yhdensuuntaiset komponentit. Kuten jäljempänä selitetään, ristitulo voidaan esittää tietynlaisen 3×3 -matriisin muodossa. Sarrus'n säännön mukaisesti tämä merkitsee, että matriisin lävistäjien suunnassa toisiaan seuraavat luvut kerrotaan keskenään.
Ristitulon laskeminen[muokkaa | muokkaa wikitekstiä]
Koordinaattimerkintä[muokkaa | muokkaa wikitekstiä]

Kolmiulotteisen avaruuden standardien kantavektorien i, j ja k ristitulot ovat oikeakätisessä koordinaatistossa seuraavat:
mistä ristitulon antikommutatiivisuuden vuoksi seuraa:
Ristitulon määritelmästä seuraa myös, että
- (nollavektori).
Voidaan osoittaa, että ristitulo noudattaa osittelulakia ja on lineaarinen, mikä tosin ei aivan mutkattomasti seuraa sen määritelmästä. Näiden ominaisuuksiensa sekä edellä lueteltujen kantavektorien ristitulojen avulla voidaan laskea minkä tahansa kahden vektorin u ja v ristitulo. Jokainen vektori voidaan nimittäin esittää kolmen kohtisuoran komponentin summana, joista kukin on yhden kantavektorin suuntainen:
Ristitulo u × v voidaan näin ollen laskea osittelulain avulla:
Tämä voidaan tulkita niin, että u × v hajotetaan yhdeksän yksinkertaisemman ristitulon summaksi, joista jokaisen tekijät ovat kantavektorien i, j ja k suuntaisia. Jokainen näistä yhdeksästä ristitulosta on helppo käsitellä, sillä ne ovat joko toistensa suuntaisia tai toisiinsa nähden kohtisuorassa. Tästä hajotelmasta saadaan edellä esitettyjen yhtälöiden avulla ja yhdistämällä samanmuotoiset termit:
mikä merkitsee, että tuloksena saatavan vektorin kolme skalaarikomponenttia s = s1i + s2j + s3k = u × v ovat
Sarakevektorien avulla sama tulos voidaan ilmaista myös seuraavasti:
Matriisimerkintä[muokkaa | muokkaa wikitekstiä]

Ristitulo voidaan muodollisesti[Huomautus 1] esittää myös determinanttina:
Tämä determinantti voidaan laskea Sarrus'n säännön tai kofaktorikehitelmän avulla. Sarrus'n säännön avulla saadaan
Jos sen sijaan käytetään kofaktorikehitelmää ensimmäiselle riville, saadaan: [6]
mistä ristitulovektorin komponentit saadaan suoraan.
Ominaisuuksia[muokkaa | muokkaa wikitekstiä]
Geometrinen merkitys[muokkaa | muokkaa wikitekstiä]


Kahden vektorin ristitulon itseisarvo on yhtä suuri kuin sellaisen suunnikkaan pinta-ala, jonka sivuina nämä vektorit ovat (katso kuvio 1):
Sellaisen suuntaissärmiön tilavuus V, jonka särmät ovat a, b ja c, voidaan laskea käyttämällä ristitulon ja pistetulon yhdistelmää, jota sanotaan skalaarikolmituloksi (katso kuvio 2):
Koska skalaarikolmitulo voi olla myös negatiivinen, suorakulmaisen särmiön tilavuus on skalaarikolmitulon itseisarvo. Esimerkiksi
Koska ristitulon itseisarvo on verrannollinen vektorien välisen kulman siniin, ristituloa voidaan käyttää kohtisuoruuden mittana samaan tapaan kuin pistetulo on yhdensuuntaisuuden mitta. Kahden yksikkövektorin ristitulon itseisarvo on 1, jos ja vain jos ne ovat kohtisuorassa, ja 0, jos ja vain jos ne ovat saman- tai vastakkaissuuntaisia. Samojen vektorien pistetulon laita on tässä suhteessa täsmälleen päinvastoin.
Vektorien komponenttiesityksen avulla voidaan myös määrittää niiden välinen kulma. Niiden pistetulo antaa tämän kulman kosinin, joka voi olla positiivinen tai negatiivinen, kun taas ristitulon itseisarvo antaa saman kulman sinin, joka on aina positiivinen.
Algebralliset ominaisuudet[muokkaa | muokkaa wikitekstiä]



- Jos kahden vektorin ristitulo on nollavektori (toisin sanoen a × b = 0), joko ainakin toinen vektoreista on nollavektori, (a = 0 ja/tai b = 0), tai vektorit ovat saman- tai vastakkaissuuntaisia (a || b), jolloin niiden välisen kulman sini on nolla ( = 0° tai = 180° ja ).
- Vektorin ristitulo itsensä kanssa on nollavektori, toisin sanoen a × a = 0.
- Ristitulo on antikommutatiivinen:
- Ristitulo noudattaa osittelulakia yhteenlaskun suhteen:
- Jos ristitulon jompikumpi tekijä kerrotaan skalaarilla, myös ristitulon arvo tulee kerrotuksi samalla skalaarilla:
- Ristitulo ei ole liitännäinen, mutta sille pätee Jacobin identiteetti:
Osoittelulaki, lineaarisuus ja Jacobin identiteetti osoittavat, että vektoriavaruus varustettuna vektorien yhteenlaskulla ja ristitulolla on Lien algebra, tarkemmin sanottuna kolmiulotteisen reaalisen ortogonaalisen ryhmän Lien algebra SO(3).
- Ristitulo ei noudata supistussääntöä: Vaikka a ei olisi nollavektori, yhtälöstä a × b = a × c ei seuraa, että b = c, vaan ainoastaan että:
Ristitulon määritelmästä seuraa, että tällöin vektorien a ja b - c välisen kulman on oltava nolla eli niiden on oltava yhdensuuntaiset. Toisin sanoen ne liittyvät toisiinsa skaalaustekijällä t, eli
jollakin skalaariarvolla t.
- Jos a · b = a · c ja a × b = a × c jollakin vektorilla a, joka ei ole nollavektori, on b = c, sillä
- and
eli b - c on sekä vektorin a suuntainen että sitä vastaan kohtisuorassa, mikä on mahdollista vain, jos b - c = 0 eli b ja c ovat identtiset.
- Geometrisen määritelmän perusteella ristitulo on invariantti rotaatiossa akselin a × b ympäri. Kaavana:
- , where on rotaatiomatriisi, jossa .
Yleisemmin ristitulo noudattaa seuraavaa identiteettiä matriisimuunnoksissa:
missä on 3×3 -matriisi ja sen käänteismatriisin transpoosi. Voidaan helposti nähdä, miten tämä kaava palautuu edelliseen, jos on rotaatiomatriisi.
Kahden ristitulon summalle pätee:
Differentioituminen[muokkaa | muokkaa wikitekstiä]
Differentiaalilaskennan tulosääntö pätee jokaiselle bilineaariselle laskutoimitukselle ja näin ollen myös ristitulolle:
missä a ja b ovat reaalimuuttujasta t riippuvia vektorifunktioita.
Kolmitulot[muokkaa | muokkaa wikitekstiä]
Ristituloa käytetään molempia kolmituloja muodostettaessa. Kolmen vektorin skalaarikolmitulo on määritelty seuraavasti:
Skalaarikolmitulo on itseisarvoltaan yhtä suuri kuin sellaisen suuntaissärmiön tilavuus, jonka sivut ovat a, b ja c, ja siinä esiintyvät vektorit voidaan vaihtaa keskenään mihin tahansa järjestykseen, joka on edellä esitetyn parillinen permutaatio. Seuraavat lausekkeet ovat näin ollen yhtä suuret:
Vektorikolmitulo on vektorin ja toisen ristitulon tuloksen ristitulo, ja sen liittää pistetuloon seuraava lause:
Vektorien järjestyksen muistamiseen tämän kaavan oikealla puolella olevassa lausekkeessa voidaan käyttää muistisääntöä "BAC miinus CAB". Tätä kaavaa käytetään fysiikassa vektoreilla suoritettavien laskutoimitusten yksinkertaistamiseen. Muuan vektorianalyysissä käyttökelpoinen, gradientteihin liittyvä erikoistapaus on:
missä on Laplacen operaattori vektoreille.
Myös seuraavat identtiset yhtälöt liittävät ristitulon skalaarikolmituloon:
- ,
missä I on identtinen matriisi.
Vaihtoehtoinen muotoilu[muokkaa | muokkaa wikitekstiä]
Ristitulon ja pistetulon yhdistää toisiinsa kaava
Tässä oikealla puolella on vektorien a' ja b Gramin determinantti, vektorien määräämän suunnikkaan pinta-alan neliö. Tämä ehto määrittää ristitulon suuruuden. Sillä jos pistetulo on määritelty vektorien välisen kulman avulla:
tämä yhtälö voidaan kirjoittaa uudestaan muotoon:
Koska Pythagoraan lauseesta seuraa, että kaikilla kulmilla pätee
- ,
saadaan tästä:
mikä on ristitulon itseisarvo ilmaistuna kulman avulla ja yhtä suuri kuin vektorien a ja b määrittämän suunnikkaan pinta-ala.
Tämä vaatimus yhdessä sen kanssa, että ristitulo on kohtisuorassa tekijöihinsä a ja b nähden tarjoaa mahdollisuuden ristitulon vaihtoehtoiseen määritelmään:[8]
Lagrangen identiteetti[muokkaa | muokkaa wikitekstiä]
Yhteyttä
voidaan verrata toiseen yhteyteen, joka liittyy tämän yhtälön oikealla puolella olevaan lausekkeeseen, nimittäin Lagrangen identiteettiin,[9]
missä a ja b voivat olla n-ulotteisia vektoreita. Tämä osoittaa, että Riemannin tilavuusmuoto pinnoille on sama asia kuin vektorianalyysin avulla laskettu tilavuusalkio. Tapauksessa n = 3 nämä kaksi yhtälöä voidaan yhdistää niin, että saadaan vektorien ristitulon itseisarvolle lauseke niiden komponenttien avulla:[10]
Sama tulos saadaan myös suoraan käyttämällä ristitulon komponentteja, jotka saadaan yhtälöstä:
Avaruudessa Lagrangen yhtälö on erikoistapaus normin multiplikatiivisuudesta kvaternioiden algebrassa: |vw| = |v||w|.
Se on myös erikoistapaus toisesta kaavasta, jota sitäkin toisinaan sanotaan Lagrangen identiteetiksi ja joka samalla on kolmiulotteinen tapaus Binet'n-Cauchyn identiteetistä:[11][12]
Jos a = c ja b = d, tämä yksinkertaistaa edellä esitettyä kaavaa.
Infinitesimaaliset generaattorit ja rotaatiot[muokkaa | muokkaa wikitekstiä]
Ristitulo kuvaa sopivasti rotaatioiden infinitesimaalisia generaattoreja avaruudessa . Erityisesti jos n on yksikkövektori avaruudessa ja R(f,,n) merkitsee rotaatiota origon kautta kulkevan, n:n määrittämän akselin ympäri kulman f verran (mitattuna radiaaneina, n:n kärjen suunnasta katsottuna vastapäivään), on
jokaiselle vektorille . Ristitulo n kuvaa näin ollen vektorin n ympäri suoritetun rotaation infinitesimaalista generaattoria. Nämä infinitesimaaliset generaattorit muodostavat Lien algebran so(3) rotaatioryhmässä SO(3), ja todetaan, että Lien algebra varustettuna ristitulolla on isomorfinen Lien algebran so(3) kanssa.
Vaihtoehtoisia tapoja ristitulon laskemiseksi[muokkaa | muokkaa wikitekstiä]
Muunnos matriisien kertolaskuksi[muokkaa | muokkaa wikitekstiä]
Vektorien ristitulo voidaan ilmaista myös antisymmetrisen matriisin ja vektorin tulona:[11]
missä yläindeksi T tarkoittaa matriisin transpoosia ja [a]× määritellään seuraavasti:
On huomattava, että [a]× on kääntyvä matriisi, jossa a on sen oikean- tai vasemmanpuoleinen nollavektori.
Jos a itsekin on ristitulo,
saadaan
Todistus korvausmenettelyllä Ristitulon kehitelmä johtaa tulokseen Tässä vasemmalla puolella oleva lauseke on yhtä suuri kuin
Toisaalta oikealla puolella oleva lauseke on,
jonka transpoosi on
Yhtälön oikea puoli voidaan saattaa muotoon
Vertailu osoittaa, että yhtälön molemmilta puolilta saatiin sama matriisi.
Geometrisen algebran avulla tämä tulos voidaan yleistää korkeampiinkin ulottuvuuksiin. Erityisesti kaikissa ulottuvuuksissa bivektori voidaan samastaa antisymmetristen matriisien kanssa, jolloin antisymmetrisen matriisin ja vektorin tulo on ekvivalentti bivektorin ja vektorin tulon ensimmäistä astetta olevan osan kanssa. Kolmessa ulottuvuudessa bivektorit ovat vektorien Hodgen duaaleja, joten tulo on ekvivalentti ristitulon kanssa, kun bivektoria käytetään sen vektoriduaalin sijasta. Korkeammissa ulottuvuuksissakin tulo voidaan laskea, mutta bivektoreilla on enemmän vapausasteita eivätkä ne ole ekvivalentteja vektorien kanssa.
Esimerkiksi epipolaarisessa geometriassa tämä merkintä on usein myös paljon helppokäyttöisempi.
Ristitulon yleisistä ominaisuuksista seuraa välittömästi, että
- and
ja siitä, että [a]× on antisymmetrinen, seuraa, että
Edellä esitetty kolmitulon bac-cab -sääntö voidaan tämän merkinnän avulla helposti todistaa.
Kuten edellä todettiin, Lien algebra varustettuna ristitulolla on isomorfinen Lien algebran so(3), kanssa, jonka alkiot voidaan samastaa antisymmetristen 3×3 -matriisien kanssa. Kuvaus a -> [a]× on isomorfismi :n ja so(3):n välillä. Tässä kuvauksessa 3-vektorien ristitulo vastaa antisymmetristen 3x3 -matriisien kommutaattoria.
Indeksimerkintä tensoreille[muokkaa | muokkaa wikitekstiä]
Ristitulo voidaan vaihtoehtoisesti määritellä Levi-Civita-symbolin eijk ja pistetulon avulla (joka ortonormaalin kannan tapauksessa on sama kuin ). Sen avulla vektorimerkintä voidaan muuttaa tensorien sovellukseksi:
missä indeksit vastaavat vektorin komponentteja. Tämä ristitulon luonnehdinta esitetään usein lyhemmin käyttämällä Einsteinin summaussääntöä
jossa toistetut indeksit arvojen 1...3 yli on laskettu yhteen. On huomattava, että tämä esitysmuoto on toinen muoto ristitulon antisymmetrisiin matriiseihin perustuvasta esitysmuodosta:
Klassisessa mekaniikassa ristitulon esittäminen Levi-Civita-symbolin avulla voi tehdä mekaaniset symmetriat ilmiselviksi, kun fysikaaliset systeemit ovat isotrooppisia. Esimerkkinä voidaan mainita hiukkanen Hooken lain mukaisessa potentiaalissa, jossa se voi värähdellä kolmessa ulottuvuudessa; mikään näistä ulottuvuuksista ei ole millään tavalla erikoisasemassa, jolloin liikemäärämomentin ristituloesitys on symmetrinen tavalla, jonka Levi-Civita-esitys tekee ilmeiseksi.
Muistisääntö[muokkaa | muokkaa wikitekstiä]
Ristitulon määritelmän muistamiseen voidaan muistisääntönä käyttää sanaa "xyzzy".
Jos
missä:
on:
Toinen ja kolmas yhtälö saadaan ensimmäisestä yksinkertaisesti kierrättämällä alaindeksit keskenään pystysuorasti, x -> y -> z -> x. Vaikeutena on luonnollisesti ensimmäisen yhtälön muistaminen, mihin on käytettävissä kaksi keinoa: on joko muistettava Sarrus'n skeeman kaksi relevanttia lävistäjää (ne, joissa 'i' esiintyy), tai on muistettava xyzzy-järjestys.
Koska Sarrus'n skeeman ensimmäinen lävistäjä on juuri edellä mainitun 3×3 -matriisin päälävistäjä, sanan xyzzy kolme ensimmäistä kirjainta on helppo muistaa.
| Tämä artikkeli tai sen osa on tuotu vieraskielisestä lähteestä ja käännös on keskeneräinen. Voit auttaa Wikipediaa tekemällä käännöksen loppuun. |
Sovelluksia[muokkaa | muokkaa wikitekstiä]
Ristituloa sovelletaan monissa yhteyksissä, esimerkiksi laskennallisessa geometriassa, fysiikassa ja insinöörialoilla. Seuraavassa mainitaan joitakin esimerkkejä sovelluksista.
Laskennallinen geometria[muokkaa | muokkaa wikitekstiä]
Ristituloa voidaan käyttää laskettaessa kahden ristikkäisen suoran etäisyys, toisin sanoen sellaisten suorien etäisyys kolmiulotteisessa avaruudessa, jotka eivät ole samassa tasossa.
Ristitulolla voidaan laskea myös kolmion tai monikulmion normaali, mitä usein tarvitaan tietokonegrafiikassa. Esimerkiksi monikulmion kiertyminen myötä- tai vastapäivään jonkin sen sisällä olevan pisteen ympäri voidaan laskea jakamalla se kolmioihin hieman pyörän puolien tapaan ja laskemalla puolien väliset kulmat yhteen, jolloin ristitulon avulla saadaan selville kunkin kulman etumerkki.
Tason laskennallisessa geometriassa ristitulon avulla voidaan määrittää kolmen pisteen , ja määräämän kulman etumerkki. Se vastaa pisteparin ja määräämien, samassa talossa olevien vektorien ristitulon suuntaa, toisin sanoen lausekkeen etumerkkiä. Jos ristitulo on nolla, pisteet ovat samalla suoralla. Käytettäessä "oikeakätisestä" koordinaattijärjestelmää nämä kolme pistettä muodostavat positiivisen pyörähdyskulman kierrossa pisteen ympäri pisteestä pisteeseen , mikäli lauseke on positiivinen, ja negatiivisen pyörähdyskulman, jos lauseke on negatiivinen.
Ristitulon avulla voidaan laskea monitahokkaiden kuten tetraedrin tai suuntaissärmiön tilavuus.
Pyörimismäärä ja vääntömomentti[muokkaa | muokkaa wikitekstiä]
Hiukkasen pyörimismäärä annetun akselin suhteen on:
missä hiukkasen paikkavektori origon suhteen ja hiukkasen liikemäärä.
Samaan tapaan pisteeseen B vaikuttavan voiman momentti pisteen A suhteen on:
Mekaniikassa voiman momenttia sanotaan myös vääntömomentiksi ja merkitään
Koska paikkavektori , liikemäärä ja voima ovat kaikki aitoja vektoreita, sekä pyörimismäärä että voiman momentti ovat pseudovektoreita eli aksiaalisia vektoreita.
Jäykkä kappale[muokkaa | muokkaa wikitekstiä]
Ristituloa käytetään usein jäykän kappaleen kuvailuun. Jäykän kappaleen kahden pisteen O ja Q välinen etäisyys pysyy vakiona, ja niiden nopeuksien välinen riippuvuus kappaleen pyöriessä on:
missä on kunkin pisteen paikkavektori, sen nopeus ja kappaleen kulmanopeus.
Koska paikkavektori ja nopeus ovat aitoja vektoreita, kun taas kulmanopeus on pseudovektori eli aksiaalinen vektori.
Lorentzin voima[muokkaa | muokkaa wikitekstiä]
Ristitulo esiintyy Lorentzin voiman lausekkeessa, joka osoittaa, kuinka suuri voima liikkuvaan sähkövaraukseen vaikuttaa sähkö- ja magneettikentässä.
Koska nopeus , voima ja sähkökentän voimakkuus ovat kaikki aitoja vektoreita, kun taas magneettivuon tiheys on pseudovektori.
Muita sovelluksia[muokkaa | muokkaa wikitekstiä]
Vektorianalyysissä vektorikentän roottori määritellään muodollisesti nablan ja vektorikentän ristitulona.
Ristitulon kirjoittaminen matriisien kertolaskun muotoon on epipolaarisessa geometriassa paljon käytetty toimenpide.
Ristitulo ulkoisena tulona[muokkaa | muokkaa wikitekstiä]
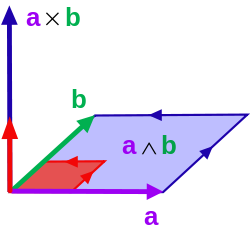
Ristituloa voidaan kuvata ulkoisen tulon käsittein. Tämä näkemys sallii ristitulon luonnollisen geometrisen tulkinnan. Ulkoisessa algebrassa kahden vektorin ulkoinen tulo (eli kiilatulo) on bivektori. Bivektori on suunnattu tasoalue pitkälti samaan tapaan kuin vektori on suunnattu jana. Kun on annettu kaksi vektoria a ja b, niiden bivektori voidaan käsittää suunnatuksi suunnikkaaksi, jonka sivuina a ja b ovat. Ristitulo saadaan tällöin ottamalla bivektorista Hodgen duaali, joka kuvaa 2-vektorit vektoreille:
Tämä voidaan käsittää suunnatuksi moniulotteiseksi alkioksi, joka on "kohtisuorassa" bivektoria vastaan. Vain kolmessa ulottuvuudessa tuloksena saadaan suunnattu jana, siis vektori, kun taas esimerkiksi neljässä ulottuvuudessa Hodgen duaali on kaksiulotteinen, siis toinen tasoalue. Niinpä vain kolmessa ulottuvuudessa vektorien a ja b ristitulo on bivektorin kanssa duaalinen vektori: se on kohtisuorassa bivektoria vastaan, sen suunta riippuu koordinaatiston kätisyydestä, ja se suuruudeltaan samassa suhteessa kohtisuoraa yksikkövektoria suurempi kuin on yksikköbivektoria suurempi, täsmälleen niin kuin sen ominaisuudet on edellä kuvattu.
Ristitulo ja kätisyys[muokkaa | muokkaa wikitekstiä]
Kun muodostetaan mitattavien suureiden ristitulo, koordinaattijärjestelmän kätisyyttä ei voida valita mielivaltaisesti. Kun kuitenkin fysiikan lait kirjoitetaan yhtälöiksi, koordinaattijärjestelmän ja myös sen kätisyyden pitäisi olla mielivaltaisesti valittavissa. Jotta tästä ei koituisi ongelmia, on oltava tarkkana, ettei koskaan kirjoiteta sellaisia yhtälöitä, joiden molemmat puolet eivät käyttäydy samoin kaikissa muunnoksissa, jotka voivat tulla kysymykseen. Jos esimerkiksi yhtälön toisella puolella on kahden vektorin ristitulo, on otettava huomioon, että jos koordinaattijärjestelmän kätisyyttä ei ole ennalta annettu, tulos ei ole (aito) vektori vaan pseudovektori. Tällöin yhteensopivuussyistä yhtälön toisenkin puolen on oltava pseudovektori.
Yleisesti ristitulo voi olla joko aito vektori tai pseudovektori riippuen siitä, kumpaa tyyppiä sen tekijät ovat. Tuloksen tyyppi riippuu sen tekijöiden tyypeistä seuraavasti:
- vektori × vektori = pseudovektori
- pseudovektori × pseudovektori = pseudovektori
- vektori × pseudovektori = vektori
- pseudovektori × vektori = vektori.
Tästä seuraa myös, että ylempänä esitetyt ortonormaalin oikeakätisen karteesisen koordinaatiston yksikkövektorien i, j ja k ristitulot edellyttävät itse asiassa, että kaikki nämä kantavektorit ovat pseudovektoreita (ellei niiden ei sallita olevan eri tyyppiä, mitä yleensä ei sallitakaan), sillä i × j = k, j × k = i and k × i = j.
Koska ristitulo saattaa olla myös (aito) vektori, se ei välttämättä vaihda suuntaansa peilauksessa tason suhteen. Näin on asian laita, jos toinen ristitulon tekijöistä on (aito) vektori ja toinen pseudovektori (toisin sanoen kahden vektorin ristitulo) Esimerkiksi kolmen aidon vektorin vektorikolmitulo on aito vektori.
Yleistyksiä[muokkaa | muokkaa wikitekstiä]
On olemassa useita tapoja yleistää ristitulon käsite useampaan ulottuvuuteen.
Lien algebra[muokkaa | muokkaa wikitekstiä]
Ristitulo on yksi yksinkertaisimmista Lien tuloista, ja näin ollen sitä yleistyksiä Lien algebrat, jotka on aksiomatisoitu binääriksi tuloiksi, jotka toteuttavat multilineaarisuuden, ristikkäissymmetrian ja Jacobin identiteetin aksioomat. On olemassa monia Lien algebroja, ja niiden tutkimuksesta on tullut laaja matematiikan ala, Lien teoria.
Esimerkiksi Heisenbergin algebra antaa toisen Lien algebran mukaisen struktuurin avaruudelle Tässä kannassa tulo on
Kvaterniot[muokkaa | muokkaa wikitekstiä]
Ristitulo voidaan esittää myös kvaternioiden termein, ja tämä onkin syynä siihen, miksi kirjaimia i, j ja k on alettu käyttää avaruuden standardien kantavektorien tunnuksina. Yksikkövektorit i, j ja k vastaavat "binäärisiä" (180 asteen) kiertoja vastaavien akselien ympäri. Näitä rotaatiota vastaavat "puhtaat" kvaterniot, joiden skalaariosa on nolla ja joiden normi on 1.
Esimerkiksi edellä esitetyt yksikkövektorien i, j, and k ristitulot vastaavat täysin kvaternioiden i, j ja k kertolaskua. Yleensäkin jos vektori [a1, a2, a3] esitetään kvaterniona a1i + a2j + a3k, kahden vektorin ristitulo saadaan laskemalla vastaavien kvaternioiden tulo ja poistamalla tuloksesta reaaliosa. Tämä reaaliosa on toisaalta sama kuin samojen vektorien pistetulon vastavektori.
Samastamalla 'puhtaasti imaginaariset kvaterniot edellä selitetyllä tavalla :n vektorien kanssa osoittautuu toisaalta, että vektorien ristitulo on puolet vastaavien kvaternioiden kommutaattorin arvosta.
Oktoniot[muokkaa | muokkaa wikitekstiä]
Seitsenulotteisten vektorien ristitulo voidaan muodostaa samaan tapaan kuin kolmiulotteistenkin käyttämällä oktonioita kvaternioiden sijasta. Se että muissa kuin kolmi- tai seitsenulotteisessa avaruudessa ei ole ei-triviaalia vektoriarvoista ristituloa, seuraa Hurwitzin lauseesta, jonka mukaan ainoat normitetut jakoalgebrat ovat 1-, 2-, 4- ja 8-ulotteiset.
Kiilatulo[muokkaa | muokkaa wikitekstiä]
Useammassa ulottuvuudessa ristitulolla ei ole suoranaista vastinetta, joka antaisi tulokseksi vektorin. On kuitenkin olemassa käsite kiilatulo, jolla on samantapaisia ominaisuuksia, paitsi että kahden vektorin kiilatulo ei ole tavallinen vektori vaan 2-vektori. Kuten edellä mainittiin, ristitulo voidaan tulkita kiilatuloksi kolmessa ulottuvuudessa käyttämällä Hodgen duaalia 2-vektorien kuvaamiseksi vektoreille. Kiilatulon Hodgen duaali antaa tuloksenaan (n - 2)-vektorin, joka on ristitulon luonnollinen yleistys missä tahansa määrässä ulottuvuuksia.
Kiilatulo ja pistetulo voidaan yhteenlaskemalla yhdistää geometriseksi tuloksi.
| Tämä artikkeli tai sen osa on tuotu vieraskielisestä lähteestä ja käännös on keskeneräinen. Voit auttaa Wikipediaa tekemällä käännöksen loppuun. |
Antisymmetriset matriisit[muokkaa | muokkaa wikitekstiä]
Jos ristitulon edellytetään olevan binäärinen laskutoimitus, sen argumentteina on oltava tarkalleen kaksi vektoria. Jos sen tuloksen ei tarvitse olla vektori tai pseudovektori vaan sen sijaan matriisi, käsite voidaan yleistää kuinka moneen ulottuvuuteen tahansa.[13][14][15]
Esimerkiksi mekaniikassa kulmanopeus voidaan tulkita joko pseudovektoriksi tai antisymmetriseksi matriisiksi eli ristikkäissymmetriseksi tensoriksi . Jälkimmäisessä tapauksessa jäykän kappaleen nopeuslaki saa muodon:
missä O määritellään muodollisesti kappaleen asemaan liittyvän pyörähdysmatriisin avulla: . Kolmessa ulottuvuudessa pätee:
Kvanttimekaniikassa pyörimismäärä eli liikemäärämomentti esitetään usein antisymmetrisenä matriisina tai tensorina. Tarkemmin sanottuna se on kappaleen paikan ja liikemäärän ristitulo:
Koska sekä :llä että :llä voisi olla mielivaltainen määrä komponentteja, tämäntyyppinen ristitulo voidaan yleistää kuinka moneen ulottuvuuteen tahansa siten, että laskutoimituksen "fysikaalinen" tulkinta säilyy.
Asian laskennallisesta puolesta kerrottiin edellä osiossa #Vaihtoehtoisia tapoja ristitulon laskemiseksi.
Historia[muokkaa | muokkaa wikitekstiä]
Vuonna 1773 italialainen matemaatikko Joseph Louis Lagrange (alkuperäiseltä nimeltään Giuseppe Luigi Lagrancia) otti käyttöön sekä piste- että ristituloksi nykyisin nimitetyt lausekkeet tutkiessaan tetraedriä kolmessa ulottuvuudessa.[16] Vuonna 1843 irlantilainen matemaattinen fyysikko Sir William Rowan Hamilton otti käyttöön kvaterniot ja niiden kertolaskun sekä samalla myös termit "vektori" ja skalaari". Jos [0, u] ja [0, v] ovat kaksi kvaternioita, joissa u ja v ovat :n vektoreita, kvaternioiden tulo on [-u · v, u × v]. James Clerk Maxwell muotoili kuuluisat sähkömagnetismin yhtälönsä alun perin Hamiltonin kvaternioiden avulla, ja tästä ja muista syistä kvaterniot kuuluivat jonkin aikaa oleellisena osana fysiikan oppimäärään.
Vuonna 1878 William Kingdon Clifford julkaisi teoksensa Elements of Dynamic (Dynamiikan alkeet), joka aikanaan oli hyvin edistyksellinen. Siinä hän määritteli kahden vektorin tulon[17] vektoriksi, joka oli suuruudeltaan yhtä suuri kuin sen suunnikkaan pinta-ala, jonka sivuina alkuperäiset vektorit ovat, ja suunta kohtisuorassa niiden muodostamaa tasoa vasten.
Englantilainen Oliver Heaviside ja Yalen yliopiston professori Josiah Willard Gibbs Connecticutissa olivat myös sitä mieltä, että kvaternioihin perustuvat laskentamenetelmät olivat liian hankalia, ja niitä käytettäessä tuloksesta oli usein merkitystä vain sen skalaari- tai vektoriosalla. Niinpä he ottivat käyttöön sekä piste- että ristitulon noin 40 vuotta kvaternioiden käyttöönoton jälkeen, mutta he saivat osakseen kiivasta vastustusta. Siihen, että uusi lähestymistapa lopulta hyväksyttiin, vaikutti paljolti sen tehokkuus, joka teki Heavisidelle mahdolliseksi yhdistää Maxwellin alkuperäisistä 20 sähkömagnetismin yhtälöistä useita siten, että jäljelle jäivät vain ne neljä, joita nykyisinkin yleisesti käytetään.[18]
Tästä kehityksestä pitkälti riippumatta ja saamatta omana aikanaan osakseen sanottavaa huomiota Hermann Grassmann kehitti geometrisen algebran, joka ei rajoittunut kahteen tai kolmeen ulottuvuuteen ja jossa ulkoisella tulolla oli keskeinen osa. Vuonna 1853 Grassmannin aikalainen Augustin-Louis Cauchy julkaisu tutkielman algebrallisista avaimista, joilla voitiin ratkaista yhtälöitä ja joilla oli samat kertolaskuominaisuudet kuin ristitulolla.[19][20] William Kingdon Clifford yhdisti Hamiltonin ja Grassmanin algebrat Cliffordin algebraksi, jossa kahden vektorin tulona saatava bivektori kolmiulotteisten vektorien tapauksessa on vektorin kaltainen ja vastaa vektorien ristituloa.
Ristitulon nimen ja merkinnän otti käyttöön Gibbs. Alun perin ne esiintyivät hänen yksityisesti opiskelijoilleen laatimassa monisteessa Elements of Vector Analysis vuodelta 1881. Käsitteen käyttökelpoisuuden mekaniikassa pani merkille Aleksandr Kotelnikov. Gibbsin merkintä ja nimitys "ristitulo" tulivat yleiseen käyttöön sen jälkeen, kun hänen entinen oppilaansa Edwin Bidwell Wilson laati oppikirjan Vector Analysis. Wilson järjesteli Gibbsin luentojen aineiston uudelleen ja yhdisti siihen aineistoa Heavisideltä, Föppsiltä ja Hamiltonilta. Hän jakoi vektorianalyysin kolmeen osaan:
»Ensimmäisenä se, mikä koskee vektorien yhteenlaskua sekä piste- ja ristituloa. Toisena se, mikä koskee differentiaali- ja integraalilaskennan yhteyksiä skalaari- ja vektorifunktioihin. Kolmantena se, mikä sisältää teorian lineaarisista vektorifunktioista.»
Kirjassa määriteltiin kahdenlaiset vektorien kertolaskut, joista käytettiin seuraavia nimiä:
- kahden vektorin suora, skalaari- eli pistetulo
- kahden vektorin ristikkäinen, vektori- eli ristitulo.
Kirjassa käsiteltiin myös useita erilaisia kolmituloja sekä useamman kuin kolmen vektorin tuloja. Edellä mainittu kolmitulon laajennus oli myös mukana.
Katso myös[muokkaa | muokkaa wikitekstiä]
- Karteesinen tulo (tulojoukko)
- Pistetulo
- Skalaarikolmitulo
- Pseudovektori
Huomautukset[muokkaa | muokkaa wikitekstiä]
- ↑ Tässä "muodollisesti" merkitsee, että tämä merkintä on determinantin muotoinen, mutta ei tarkkaan ottaen ole determinantin määritelmän mukainen; kyseessä on lähinnä ristitulon kehitelmän muistamiseksi laadittu muistisääntö.
Lähteet[muokkaa | muokkaa wikitekstiä]
- Florian Cajori: A History Of Mathematical Notations Volume II, s. 134. Open Court Publishing, 1929. ISBN 978-0-486-67766-8. Teoksen verkkoversio.
- E. A. Milne: ”2. luku, Vector Product”, Vectorial Mechanics, s. 11–31. Methuen Publishing, 1948.
- Edwin Bidwell Wilson: Vector Analysis: A text-book for the use of students of mathematics and physics, founded upon the lectures of J. Willard Gibbs. Yale University Press, 1901. Teoksen verkkoversio.
- T. Levi-Civita, U. Amaldi: Lezioni di meccanica razionale. Bologna: Zanichelli editore, 1949. (italiaksi)
Viitteet[muokkaa | muokkaa wikitekstiä]
- ↑ WS Massey: Cross products of vectors in higher dimensional Euclidean spaces. The American Mathematical Monthly, 1983, 90. vsk, nro 10, s. 697–701. doi:10.2307/2323537.
- ↑ H. Jeffreys, BS.: Methods of mathematical physics. Cambridge University Press, 1999. Teoksen verkkoversio.
- ↑ Edwin Bidwell Wilson: Vector Analysis: A text-book for the use of students of mathematics and physics, s. 60–61. Yale University Press, 1901.
- ↑ Dennis G. Zill, Michael R. Cullen: ”Definition 7.4: Cross product of two vectors”, Advanced engineering mathematics, 3. painos, s. 324. . ISBN 0-7637-4591-X. Teoksen verkkoversio.
- ↑ a b A History of Vector Analysis math.ucdavis.edu.
- ↑ Dennis G. Zill, Michael R. Cullen: ”Equation 7: a × b as sum of determinants”, Advanced engineering mathematics, s. 321. Jones & Bartlett Learning, 2006. ISBN 0-7637-4591-X. Teoksen verkkoversio.
- ↑ M. R. Spiegel, S. Lipschutz, D. Spellman: Vector Analysis, s. 29. McGraw Hill, 2009. ISBN 978-0-07-161545-70.
- ↑ WS Massey: Cross products of vectors in higher dimensional Euclidean spaces. The American Mathematical Monthly, joulukuu 1983, 90. vsk, nro 10, s. 697–701. doi:10.2307/2323537. JSTOR 2323537.
- ↑ Vladimir A. Boichenko, Gennadii Alekseevich Leonov, Volker Reitmann: Dimension theory for ordinary differential equations, s. 26. Viewer+Teubner Verlag, 2005. ISBN 3-519-00437-2.
- ↑ Pertti Lounesto: Clifford algebras and spinors, 2. painos. Cambridge University Press, 2001. ISBN 0-521-00551-5. Teoksen verkkoversio. [vanhentunut linkki]
- ↑ a b Shuangzhe Liu and Gõtz Trenkler: Hadamard, Khatri-Rao, Kronecker and other matrix products. Int J Information and systems sciences, 2008, 4. vsk, nro 1, s. 160–177. Institute for scientific computing and education. Artikkelin verkkoversio (pdf). (Arkistoitu – Internet Archive)
- ↑ Eric W. Weisstein: ”Binet-Cauchy identity, 2. painos”, CRC concise encyclopedia of mathematics, s. 228. CRC Press, 2003. ISBN 1-58488-347-2. Teoksen verkkoversio.
- ↑ Generalizing Cross Products and Maxwell's Equations to Universal Extra Dimensions arxiv.org. 2006.
- ↑ C.A. Gonano: Estensione in N-D di prodotto vettore e rotore e loro applicazioni. Politecnico di Milano, Italy., 2011. Teoksen verkkoversio.
- ↑ Cross product in N Dimensions – the doublewedge product C.A. Gonano, R.E. Zich.
- ↑ Lagrange, J. L.: ”Solutions analytiques de quelques problèmes sur les pyramides triangulaires”, Oeuvres, 3. osa. , 1773.
- ↑ William Kingdon Clifford: Elements of Dynamic, Part I, s. 95. MacMillan & Co, 1878. Teoksen verkkoversio.
- ↑ Paul J. Nahin: Oliver Heaviside: the life, work, and times of an electrical genius of the Victorian age, s. 108–109. JHU Press, 2000. ISBN 0-8018-6909-9.
- ↑ Michael J. Crowe: A History of Vector Analysis, s. 83. DOver, 1994. ISBN 0-486-67910-1.
- ↑ Augustin-Louis Cauchy: Oeuvres, 12. osa, s. 16. , 1999. Teoksen verkkoversio.
Kirjallisuutta[muokkaa | muokkaa wikitekstiä]
- Kivelä, Simo K.: Algebra ja geometria. Espoo: Otatieto, 1989. ISBN 951-672-103-6.
- Rikkonen, Harri: Matematiikan pitkä peruskurssi I: Vektorialgebra ja analyyttinen geometria. Helsinki: Otakustantamo, 1969. ISBN 951-671-067-0.
- Pitkäranta, Juhani: Calculus Fennicus – TKK:n 1. lukuvuoden laaja matematiikka (2000–2013) (pdf) Helsinki: Avoimet oppimateriaalit ry. ISBN 978-952-7010-12-9 ISBN 978-952-7010-6 (pdf).
Aiheesta muualla[muokkaa | muokkaa wikitekstiä]
- Hazewinkel, Michiel (toim.): ”Cross product”, Encyclopedia of Mathematics. Springer, 2001. ISBN 978-1-55608-010-4. Teoksen verkkoversio.
- Cross product Wolfram MathWorld. Eric W. Weisstein.
- The Dot and Cross Procudts Eli Lansey.
- Cross product in N Dimensions – the doublewedge product (pdf) 2014. C.A. Gonano and R.E. Zich, Polytehcnic University of Milan.
- Real and Complex Products of Complex Numbers cut-the-knot.org.
- Cross-Products and Rotations in Euclidean 2- and 3-Space (pdf) 2007. W. Cahan, University of California, Berkeley.



























































![{\displaystyle \mathbf {a} \times \mathbf {b} =[\mathbf {a} ]_{\times }\mathbf {b} ={\begin{bmatrix}\,0&\!-a_{3}&\,\,a_{2}\\\,\,a_{3}&0&\!-a_{1}\\-a_{2}&\,\,a_{1}&\,0\end{bmatrix}}{\begin{bmatrix}b_{1}\\b_{2}\\b_{3}\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0fe5f2ef2ad4f1683fe47d483c4ce3e900f419f5)
![{\displaystyle \mathbf {a} \times \mathbf {b} =[\mathbf {b} ]_{\times }^{\mathrm {T} }\mathbf {a} ={\begin{bmatrix}\,0&\,\,b_{3}&\!-b_{2}\\-b_{3}&0&\,\,b_{1}\\\,\,b_{2}&\!-b_{1}&\,0\end{bmatrix}}{\begin{bmatrix}a_{1}\\a_{2}\\a_{3}\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/121d5aedd8549ca91c624e9c862711aa81962e34)
![{\displaystyle [\mathbf {a} ]_{\times }{\stackrel {\rm {def}}{=}}{\begin{bmatrix}\,\,0&\!-a_{3}&\,\,\,a_{2}\\\,\,\,a_{3}&0&\!-a_{1}\\\!-a_{2}&\,\,a_{1}&\,\,0\end{bmatrix}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/614cc7fd18f2f2e212803822f31acb2505c98c89)

![{\displaystyle [\mathbf {a} ]_{\times }=\mathbf {d} \mathbf {c} ^{\mathrm {T} }-\mathbf {c} \mathbf {d} ^{\mathrm {T} }.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7bebe8181aeb49a3e8987339594fd7de7c454a9)

![{\displaystyle [\mathbf {a} ]_{\times }={\begin{bmatrix}0&c_{2}d_{1}-c_{1}d_{2}&c_{3}d_{1}-c_{1}d_{3}\\c_{1}d_{2}-c_{2}d_{1}&0&c_{3}d_{2}-c_{2}d_{3}\\c_{1}d_{3}-c_{3}d_{1}&c_{2}d_{3}-c_{3}d_{2}&0\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ff95aa2908dc95252f1a28c8a9167458c98c993)



![{\displaystyle [\mathbf {a} ]_{\times }\,\mathbf {a} =\mathbf {0} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e918b623a3b34134199284e350a5a06f8fe0305)
![{\displaystyle \mathbf {a} ^{\mathrm {T} }\,[\mathbf {a} ]_{\times }=\mathbf {0} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/3cd1a98ffd5ab228553c458345bb26af8422bb43)
![{\displaystyle \mathbf {b} ^{\mathrm {T} }\,[\mathbf {a} ]_{\times }\,\mathbf {b} =0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c23cfb35b83ca69742e7da1381a7477a18d04e4d)





![{\displaystyle \eta ^{mi}\varepsilon _{ijk}a^{j}=[\mathbf {a} ]_{\times }.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f337c326ad2b755913fd5d9ffbd88daab6bfad44)
































![{\displaystyle [x,y]=z,[x,z]=[y,z]=0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf27588f0b4586bd6a22e7e3d7c9d8513219e3ea)





![{\displaystyle \Omega =[\omega ]_{\times }={\begin{bmatrix}\,\,0&\!-\omega _{3}&\,\,\,\omega _{2}\\\,\,\,\omega _{3}&0&\!-\omega _{1}\\\!-\omega _{2}&\,\,\omega _{1}&\,\,0\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/05e0047b97afd82fad69c347f1c4ec89e9635d5e)





