Trigonometrinen funktio
Trigonometriset funktiot ovat matematiikassa kulman funktioita, jotka ovat tärkeitä, kun tutkitaan kolmioita tai mallinnetaan jaksollisia ilmiöitä. Trigonometriset funktiot määritellään yleisesti kulman sisältävän suorakulmaisen kolmion sivujen suhteina, mutta ne voidaan yhtäpitävästi määritellä yksikköympyrään piirrettyjen janojen pituuksina.[1] Modernimmat määritelmät esittävät ne sarjoina tai tiettyjen differentiaaliyhtälöiden ratkaisuina, jolloin ne voidaan laajentaa käsittämään sekä positiiviset että negatiiviset luvut ja jopa kompleksiluvut. Kaikki nämä lähestymistavat esitellään edempänä.
Nykyään on käytössä kuusi trigonometrista perusfunktiota, jotka on taulukoitu alempana keskinäisine yhteyksineen. Näitä yhteyksiä pidetään usein varsinkin neljän viimeisen funktion määritelmänä, mutta ne voidaan määritellä yhtä hyvin myös geometrisesti tai muilla tavoilla ja johtaa sitten funktioiden väliset yhteydet.
| Funktio | Lyhenne | Yhteydet |
| Sini | sin | |
| Kosini | cos | |
| Tangentti | tan | |
| Kotangentti | cot | |
| Sekantti | sec | |
| Kosekantti | csc (tai cosec) |
Ennen oli käytössä myös muutama nykyään vähän käytetty funktio, joiden arvoja myös taulukoitiin, kuten:
- versaalisini:
- ekssekantti:
Myös sekantti ja kosekantti ovat harvoin käytettyjä, sillä niiden sijasta käytetään yleensä sinin ja kosinin käänteisarvoja.
Trigonometristen funktioiden tiettyjen rajoittumien käänteisfunktioita ovat arkusfunktiot.
Määritelmät suorakulmaisen kolmion avulla[muokkaa | muokkaa wikitekstiä]

Määritelläksemme trigonometriset funktiot kulmalle α, aloitamme mielivaltaisesta suorakulmaisesta kolmiosta, jonka terävistä kulmista toiselle käytetään merkintää α (0 < α < 180°). Suoran kulman vastainen sivu on hypotenuusa, mitä merkitsemme myös h:lla. Vastainen kateetti on tarkastelemamme kulman vastainen sivu eli a. Viereinen kateetti on suoran kulman ja tarkastelemamme kulman välinen sivu eli b.
Oletamme kaikkien kolmioiden olevan euklidisella tasolla, jolloin kolmion sisäkulmien summa on 180°. Tällöin suorakulmaisen kolmion terävät kulmat ovat molemmat välillä 0° < θ < 90°, missä θ on kulma. Määrittelemmekin nyt tässä trigonometriset funktiot vain näille kulmille, laajempia määritelmiä esittelemme tuonnempana.
Kulman sini on vastaisen kateetin ja hypotenuusan pituuksien suhde. On huomattava, että tämä suhde riippuu vain kulmasta α, sillä kaikki suorakulmaiset kolmiot, joissa on kulma α, ovat yhdenmuotoisia. Kulman kosini on viereisen kateetin ja hypotenuusan pituuksien suhde. Kulman tangentti on vastaisen ja viereisen kateetin pituuksien suhde. Määritelmistä saamme seuraavat kaavat:
Jäljellä oleville kolmelle funktiolle on helpointa antaa määritelmät äsken laatimiemme määritelmien avulla. Kulman kosekantti on kulman sinin käänteisluku eli hypotenuusan ja vastaisen kateetin pituuksien suhde. Kulman sekantti on kulman kosinin käänteisluku eli hypotenuusan ja viereisen kateetin pituuksien suhde. Kulman kotangentti on kulman tangentin käänteisluku eli viereisen ja vastaisen sivun pituuksien suhde. Saamme kaavat:
Kun kulma on hyvin lähellä nollaa tai suoraa kulmaa, kolmio on muodoltaan hyvin kapea. Tällöin siinä toinen kateetti on hyvin lyhyt ja toinen melkein hypotenuusan pituinen. Tällä perusteella laajennamme antamaamme trigonometristen funktioiden määritelmiä rajatapauksina myös 0 ja 90 asteen kulmille seuraavasti:
Nollan asteen kulmalle ei voida määritellä kotangenttia eikä sekanttia eikä liioin 90 asteen kulmalle tangenttia eikä kosekanttia. Kulman lähestyessä näitä arvoja näiden funktioiden arvot kasvavat rajattomasti, minkä vuoksi funktioilla sanotaan näissä kohdissa olevan raja-arvo ääretön.
Määritelmät yksikköympyrän avulla[muokkaa | muokkaa wikitekstiä]
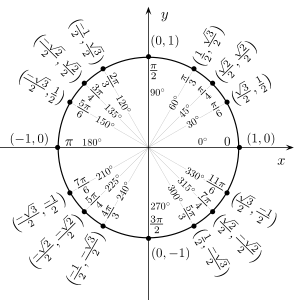
Trigonometriset funktiot voidaan myös määritellä yksikköympyrän eli origossa sijaitsevan ympyrän, jonka säde on 1, avulla. Tämä määritelmä ei juuri eroa aiemmasta suorakulmaisten kolmioiden avulla tehdystä, sillä se tukeutuu vahvasti suorakulmaisiin kolmioihin. Yksikköympyrän etu on kuitenkin se, että se sallii trigonometristen funktioiden määrittelyjoukon luontevan laajentamisen kaikille positiivisille ja negatiivisille kulmille sen sijaan, että hyväksyttäisiin kulman arvot ainoastaan välillä 0° < θ < 90°.
Piirretään origon kautta kulkeva suora, joka muodostaa positiivisen x-akselin kanssa kulman θ. Suora leikkaa yksikköympyrän kahdessa pisteessä, joista toinen on x-akselin ylä- ja toinen alapuolella (tai erikoistapauksessa, kun θ=0, pisteissä (-1,0) ja (1,0)). Olkoon toinen näistä leikkauspisteistä (x,y). Tällöin määritellään, että tämän pisteen x-koordinaatti on kulman θ kosini ja y-koordinaatti sen sini, eli
- .
Jos kulma on muodostettu kiertämällä leikkauspisteestä (1,0) lähdettäessä vastapäivään, kulma θ katsotaan positiiviseksi, myötäpäivään kierrettäessä negatiiviseksi. Koska yksikköympyrän yhtälö on:
- ,
seuraa tästä, että kaikilla θ:n arvoilla pätee
- .
Tämä yhtälö on itse asiassa sama kuin Pythagoraan lause trigonometristen funktioiden avulla ilmaistuna.
Kuvassa on annettu joitain tavallisia kulmien arvoja radiaaneissa. Vastapäivään tehdyt mittaukset ovat positiivisia ja myötäpäivään tehdyt negatiivisia kulmia.
Yksikköympyrän sisälle piirretty kolmio vahvistaa, että jos kulma θ on terävä, tämä määritelmä on yhtäpitävä aikaisemman, suorakulmaiseen kolmioon perustuvan määritelmän kanssa: kolmion hypotenuusa on ympyrän säde, jonka pituus on 1, joten sin θ = y/1 ja cos θ = x/1. Yksikköympyrää voi ajatella tapana tarkastella ääretöntä määrää suorakulmaisia kolmioita vaihtelemalla sivujen pituuksia mutta pitämällä hypotenuusa yhtäsuurena.
Yksikköympyrään perustuva määritelmä ei kuitenkaan edellytä, että kulman on oltava terävä. Kuviosta voidaan todeta, että jos pisteestä (1,0) lähdetään ympyrän kehää pitkin vastapäivään kulman θ tai edelleen kulman 180°-θ verran, pisteet, joihin päädytään, ovat toistensa peilikuvia y-akselin eli suoran x=0 suhteen. Koska näiden pisteiden koordinaatit ovat (cos θ, sin θ) ja (cos (180°-θ), sin (180°-θ), seuraa tästä, että
- ja
- ,
tai jos kulmayksikkönä käytetään radiaania,
- ja
Jos taas kulma θ korvataan kulmalla -θ, päädytään pisteeseen, joka on alkuperäisen pisteen peilikuva x-akselin suhteen. Siitä seuraa, että
- ja
- .
Tämä merkitsee, että kosini on parillinen, sini sen sijaan pariton funktio.
Muut trigonometriset funktiot määritellään sinin ja kosinin suhteina tai käänteisarvoina samoin kuin suorakulmaista kolmiota lähtökohtana käytettäessäkin voitaisiin tehdä:
- ,
- ,
- ,
- ,

Kulmilla, jotka ovat suurempia kuin täysikulma tai pienempiä kuin , trigonometriset funktiot määritellään antamalla kulman kiertyä ympäri. Toisin sanoen, jos ympyrän kehää pitkin kuljetaan kulman verran, ajatellaan, että on tehty ensin täysi kierros ja sen jälkeen jatkettu vielä kulman verran, jolloin päädytään samaan pisteeseen kuin jos olisikin kierretty vain kulman verran. Tällä tavalla laajennetut sini ja kosini ovat siis jaksollisia funktioita, joiden jakso on .
kaikille kulman arvoille θ ja kokonaisluvuille n.
Sinillä, kosinilla ja tangentilla on kaikilla äärettömästi nollakohtia seuraavasti, kun kulma on θ ja n on kokonaisluku:
Jaksollisen funktion pienintä positiivista jaksoa sanotaan funktion perusjaksoksi. Sinin, kosinin, sekantin ja kosekantin kokonainen ympyrä eli radiaania tai 360 astetta; tangentin perusjakso on puoliympyrä eli radiaania tai 180 astetta. Yllä määriteltiin vain sini ja kosini suoraan yksikköympyrän avulla, sillä neljä muuta trigonometrista funktiota voidaan määritellä niiden avulla:

Oikealla olevassa kuvassa on sinin ja kosinin kuvaajista huomattavasti poikkeava tangenttifunktion kuvaaja piirrettynä koordinaatistoon. Huomaa, että sen x-akselin leikkauspisteet vastaavat sinifunktion vastaavia, kun taas ne arvot joilla se ei ole määritelty vastaavat kosinifunktion nollakohtia. Funktion arvot muuttuvat hitaasti lähellä kulman arvoja ja nopeasti kulmilla jotka ovat lähellä arvoja . Tangentilla on pystysuora asymptootti :n arvoilla . Tämä johtuu siitä, että kulman arvon lähestyessä arvoa vasemmalta lähestyy funktion arvo ääretöntä, kun taas oikealta lähestyttäessä sen arvo lähestyy miinus ääretöntä.

Kaikki trigonometriset funktiot voidaan vaihtoehtoisesti määritellä O-keskisen yksikköympyrän (kuvattu oikealla) avulla, ja vastaavanlaisia geometrisia määritelmiä käytettiinkin ennen paljon. Ympyrän jänteelle AB, jossa θ on puolet kolmion OAB janan AB vastaisesta kulmasta, sin(θ) on AC (puolet jänteestä); määritelmä, jonka esitti intialainen matemaatikko Aryabhata 400-luvun lopulla. cos(θ) on vaakasuora jana OC, ja versin(θ) = 1 − cos(θ) on jana CD. tan(θ) on ympyrän pisteeseen A piirretylle tangentille piirretyn janan AE pituus, minkä takia funktio onkin nimetty tangentiksi. cot(θ) on jana AF, joka on myös pisteen A kautta kulkevalla tangentilla. sec(θ) ja csc(θ) ovat sekanttien osia, ja niitä voidaan myös pitää janan OA projektioina x- ja y-akseleille pisteeseen A piirrettyä tangenttia pitkin. DE on exsec(θ) = sec(θ) − 1 (sekantin ympyrän ulkopuolinen osa). Näissä konstruktioista on helppoa nähdä, että tangentti- ja sekanttifunktiot hajaantuvat, kun θ lähestyy suoraa kulmaa, ja että kosekantti ja kotangentti hajaantuvat θ:n lähestyessä nollaa. (Moni muu vastaava rakennelma on mahdollinen, ja yksinkertaiset trigonometriset identiteetit voidaan todistaa graafisesti.)
Jos kulma θ on hyvin pieni, on sitä vastaava kaari (arc oheisessa kuviossa) vain hieman pidempi kuin tämän kulman vastainen kateetti, jonka pituus on sin θ. Mitä pienempi kulma θ on, sitä tarkemmin nämä ovat yhtä pitkiä, eli niiden suhde on sitä lähempänä arvoa 1. Tähän liittyen voidaankin osoittaa, että kun kulmayksikkönä käytetään radiaania, on
- .
Todistus[muokkaa | muokkaa wikitekstiä]
Todistetaan tapaus , tapaus todistetaan vastaavalla tavalla.
Koska ympyrän jänne on lyhyempi kuin sen määrittämä kaari, niin sinifunktion määritelmän ja tasakylkisen kolmion huippukulman puolittajan ominaisuuksien nojalla pätee . Kun ja , niin .
Yksikköympyrän sektori, jonka määrittää kulma on puolestaan pienempi kuin suorakulmainen kolmio, jonka kateetin pituus on ja viereinen kulma . Siis tangenttifunktion määritelmän nojalla saadaan , joka on yhtäpitävä epäyhtälön kanssa. Koska , kun , niin .
Yhdistettynä edellinen jänteen ja kaaren pituuksista johdetun epäyhtälön kanssa saadaan . Koska , niin kuristuslauseen nojalla .
Seuraus[muokkaa | muokkaa wikitekstiä]
, sillä , kun on :n lähellä, joten .
Tätä ja edellistä raja-arvoa sekä trigonometristen funktioiden yhteenlaskukaavoja käytetään johdettaessa - ja muiden trigonometristen funktioiden derivaattoja.
Määritelmät sarjakehitelmien avulla[muokkaa | muokkaa wikitekstiä]

Huomautus: Kuten differentiaalilaskennassa yleensäkin, kaikkien kulmien arvot ilmoitetaan tässä radiaaneina. (Katso otsikko radiaanien merkitys)
Pelkällä geometrialla ja raja-arvoilla voidaan osoittaa, että sinin derivaatta on kosini, ja että kosinin derivaatta on sinin vastaluku. Taylorin polynomien avulla voidaan näyttää että seuraavat identiteetit pätevät kaikille reaaliluvuille x:
Näitä identiteettejä käytetään usein sinin ja kosinin määritelminä ja lähtöpisteenä trigonometristen funktioiden ja niiden sovellusten (esim. Fourier-sarjoissa) täsmälliselle käsittelylle, sillä sarjojen teoria voidaan rakentaa reaalilukujen pohjalta, ilman minkäänlaisia geometrisia tulkintoja. Näiden funktioiden derivoituvuus ja jatkuvuus todentuu näin sarjojen määritelmien pohjalta.
Muillekin funktioille on olemassa sarjakehitelmiä (Abramowitz ja Stegun 1964, Weisstein 2006):
Kun tämä sarja esitetään muodossa, jossa nimittäjät ovat vastaavia kertomia, saavat osoittajat, joita kutsutaan "tangenttiluvuiksi", kombinatoriaalisen tulkinnan: ne ovat äärellisten parittomasti mahtavien joukkojen vuorottelevien permutaatioiden lukumäärä.
Kun tämä sarja esitetään muodossa, jossa nimittäjät ovat vastaavia kertomia, saavat osoittajat, joita kutsutaan "sekanttiluvuiksi", kombinatoriaalisen tulkinnan: ne ovat äärellisten parillisesti mahtavien joukkojen vuorottelevien permutaatioiden lukumäärä.
missä
- on n:s Bernoullin luku,
- on n:s Eulerin luku, ja
- on n:s ylös/alas-luku.
Kompleksianalyysissä käytetyn teoreeman mukaan tällä funktiolla on yksikäsitteinen analyyttinen laajennus kompleksilukujen alueelle. Sen Taylorin polynomi on sama kuin reaaliluvuille määritelty, joten trigonometriset funktiot on määritelty kompleksiluvuille käyttämällä yllä olevia Taylorin sarjoja.
Suhde eksponenttifunktioon ja kompleksilukuihin[muokkaa | muokkaa wikitekstiä]
Eksponenttifunktiolle voidaan johtaa Taylorin sarjakehitelmä:
Tämä on alun perin johdettu vain muuttujan x reaaliarvoille. Tämä kehitelmä tekee kuitenkin mahdolliseksi laajentaa eksponenttifunktiota niin, että se on määritelty silloinkin, kun x on mielivaltainen kompleksiluku: otetaan vain yllä oleva kehitelmä funktion määritelmäksi. Tällöin osoittautuu, että trigonometriset funktiot ja eksponenttifunktio liittyvät kompleksialueella läheisesti toisiinsa: kosini- ja sinifunktio ovat eksponenttifunktion reaali- ja imaginaariosa, kun muuttuja on puhtaasti imaginaarinen:
Tämän yhteyden huomasi ensimmäisenä Leonhard Euler, ja sitä kutsutaan hänen mukaansa Eulerin lauseeksi. Tämän lauseen seurauksena trigonometrisista funktioista tulee oleellinen osa kompleksianalyysin geometrista tulkintaa. Esimerkiksi kompleksitasolle piirretty yksikköympyrä, jonka määrittelee kaava , voidaan parametrisoida sinin ja kosinin avulla, jolloin kompleksiarvoisten eksponenttifunktioiden ja trigonometristen funktioiden välinen yhteys muuttuu entistä selvemmäksi.
Eulerin kaavan avulla voidaan lisäksi määritellä trigonometriset funktiot kompleksiargumenteilla :
missä .[2]
Lisäksi kaikille reaalisille :
Funktioiden käyttäytyminen kompleksitasossa[muokkaa | muokkaa wikitekstiä]
Funktio ei saavuta ääretöntä missään äärellisessä pisteessä, mutta funktio lähenee sitä raja-arvona, jos lähestyy ääretöntä siten, että sen imaginääriosa kasvaa kohti ääretöntä tai pienenee kohti miinusääretöntä. Tästä seuraa, että ääretön on siis funktion asymptoottinen arvo. Edelläesitetty pätee myös funktiolle , koska sinin arvot saadaan kosinin arvoista siirtämällä niitä x-akselin suuntaan :n verran.[4]
Määritelmät differentiaaliyhtälöiden avulla[muokkaa | muokkaa wikitekstiä]
Sini- ja kosinifunktio toteuttavat differentiaaliyhtälön
toisin sanoen kumpikin on oman toisen derivaattansa vasta-alkio. Kaksiulotteisessa lineaariavaruudessa V, joka koostuu tämän yhtälön kaikista ratkaisuista, sinifunktio saadaan alkuehdoilla ja , ja kosinifunktio saadaan alkuehdoilla ja . Koska sini ja kosini ovat lineaarisesti riippumattomia, muodostavat ne V:n kannan. Tämä tapa määritellä trigonometriset funktiot on olennaisesti sama kuin Eulerin kaavan avulla tehty määritelmä. Tätä differentiaaliyhtälöä voi myös käyttää sinin ja kosinin trigonometristen kaavojen todistamiseen.
Tangenttifunktio on epälineaarisen differentiaaliyhtälön
yksiselitteinen ratkaisu alkuarvoilla .
Radiaanien merkitys[muokkaa | muokkaa wikitekstiä]
Radiaanit määrittelevät kulman mittaamalla yksikköympyrän kehää pitkin kuljettua matkaa ja ovat trigonometristen funktioiden luonnollinen muuttuja. Ainoastaan ne sini- ja kosinifunktiot, jotka kuvaavat radiaanit suhteiksi, toteuttavat ne differentiaaliyhtälöt, jotka tavallisesti kuvaavat niitä. Jos sinin tai kosinin muuttujan "taajuutta" muutetaan,
muuttuu derivaattojen "amplitudi".
- .
Vakio on muunnoskerroin yksiköstä toiseen. Jos on ilmoitettu asteissa,
Sinin toinen derivaatta ei siis toteuta differentiaaliyhtälöä
- ,
vaan yhtälön
- ;
kosinifunktio käyttäytyy samalla tavoin.
Nämä sinit ja kosinit ovat siis eri funktioita, ja sinin neljäs derivaatta on sini vain, jos muuttuja on radiaaneissa.
Muita määritelmiä[muokkaa | muokkaa wikitekstiä]
Matemaattisessa analyysissä trigonometriset funktiot voidaan määritellä abstraktisti seuraavien perusominaisuuksiensa avulla. Olkoot s(x) ja c(x) kaksi reaalimuuttujan reaaliarvoista funktiota, joilla on seuraavat ominaisuudet:
- . Funktiot s(x) ja c(x) on määritelty kaikilla arvoilla
- . s(0) = 0 ja c(0) = 1.
- . kaikilla
- . Kaikilla arvoilla pätevät seuraavat funktioiden yhteen- ja vähennyslaskukaavat:
- s (x+y) = s(x)c(y) + c(x)s(y)
- c (x+y) = c(x)c(y) - s(x)s(y)
- :.
Tällöin funktiota s sanotaan sinifunktioksi ja merkitään , ja vastaavasti funktiota c sanotaan kosinifunktioksi ja merkitään .[5]
Vaikka tämän määritelmän nojalla ei olekaan heti selvää, onko tällaisia funktiota ylipäänsä olemassa tai ovatko ne yksikäsitteisesti määritellyt, voidaan siitä kuitenkin johtaa trigonometristen funktioiden muut ominaisuudet. Väliarvolauseen avulla voidaan esimerkiksi todistaa, että tällaiset funktiot ovat jaksollisia[6]. Niin ikään voidaan osoittaa, että nämä funktiot ovat derivoituvia ja että
- ja
- .[7]
Derivaattojen avulla voidaan edelleen johtaa näiden funktioiden Taylorin sarjat, ja tällöin todetaan, että tämä funktioiden ominaisuuksiin perustuva määritelmä on yhtäpitävä sarjakehitelmiin perustuvan määritelmän kanssa.[8]
Edelleen voidaan todistaa, että jos yksikköympyrältä valitaan sellainen piste (x0,y0), että tämän pisteen ja pisteen (1,0) välisen kaaren pituus on s, niin ja . Tämä osoittaa, että tämä abstrakti määritelmä on myös yhtäpitävä funktioiden geometrisen, yksikköympyrään perustuvan määritelmän kanssa.[8]
Trigonometristen funktioiden ominaisuuksia ja muunnoskaavoja[muokkaa | muokkaa wikitekstiä]
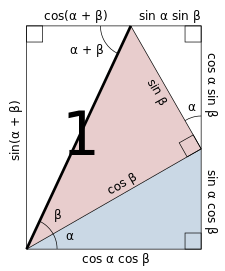
Trigonometristen funktioiden monet tärkeimmät ominaisuudet voidaan johtaa sinin ja kosinin yhteen- ja vähennyslaskukaavoista. Näistä voidaan johtaa vastaavat kaavat myös tangentille ja kotangentille:
Näiden avulla voidaan johtaa edelleen myös seuraavat muunnoskaavat:
Trigonometristen funktioiden tarkkoja arvoja[muokkaa | muokkaa wikitekstiä]
- Katso myös: Rationaalinen trigonometria

Yleensä trigonometrisen funktion arvoa ei voida esittää tarkasti, mutta joillekin erityisarvoille tämä onnistuu helposti käyttämällä Pythagoraan lausetta apuna. Esitämme näistä arvoista muutamia ja kaksi ns. muistikolmiota, joiden avulla voi tarkkoja arvoja laskea käsin.
Neliön lävistäjä jakaa neliön kahteen yhtä suureen suorakulmaiseen ja tasakylkiseen kolmioon. Näissä molemmissa kateetit ovat yhtä pitkät ja kulmat 45°-45°-90°. Pythagoraan lauseen mukaan neliön lävistäjän ja sivun suhde on √2. Nyt kun suorakulmaisen kolmion kaikkien sivujen pituudet tunnetaan, voidaan trigonometristen funktioiden tarkka arvo laskea määritelmien avulla.
Tasasivuisen kolmion kaikki kulmat ovat suuruudeltaan 60°. Jakamalla tämä kolmio kahtia korkeusjanalla, syntyy kaksi suorakulmaista kolmiota, joiden kulmat ovat 30°-60°-90° ja lyhyemmän kateetin pituus on puolet hypotenuusasta. Pythagoraan lauseesta seuraa, että pidemmän kateetin pituus on √3/2 kertaa hypotenuusan pituus.
Näiden sekä edellä jo mainittujen yhteen- ja vähennyslaskukaavojen avulla trigonometristen funktioiden tarkat arvot voi johtaa monille muillekin kulmille, kuten kaikille kulmille, joiden asteluku on kolmen monikerta. Käytännössä lausekkeista tulee melko monimutkaisia.
Derivaatat ja integraalit[muokkaa | muokkaa wikitekstiä]
Trigonometristen funktioiden derivaatat voidaan johtaa niiden yhteen- ja vähennyslaskukaavojen avulla. Tällöin on kulmayksikkönä käytettävä radiaania. Ohessa on myös sinin, kosinin ja tangentin integraalit.
Todistus[muokkaa | muokkaa wikitekstiä]
Todistetaan tulos , tulos todistetaan vastaavalla tavalla.
(yhteenlaskukaavan nojalla) (edellä todistettujen raja-arvojen nojalla) .
Käänteisfunktiot[muokkaa | muokkaa wikitekstiä]
- Pääartikkeli: Arkusfunktiot
Trigonometriset funktiot ovat jaksollisia, joten niiden määrittelyjoukkoa täytyy rajoittaa, jotta niille olisi mahdollista määritellä käänteisfunktio. Seuraavassa taulukossa oikealla olevat yhtälöt määrittelevät vasemmalla olevan funktion; nämä eivät siis ole johdettuja kaavoja. Käänteisfunktiot, joista käytetään nimitystä arkusfunktiot, määritellään yleensä seuraavalla tavalla:
Trigonometrisille funktioille on mahdollista määrittää käänteisfunktiot myös mille tahansa jakson pituiselle monotoniselle välille. Joskus käytetään merkintää, jossa käänteisfunktion nimen alkuosan päällä on viiva, korostamaan sitä, että määrittely on tehty funktion päähaaran mukaan. Esimerkiksi . Tällainen merkintätapa on kuitenkin harvinainen.
Trigonometristen funktioiden käänteisfunktioille käytetään joskus merkintätapaa sin−1(x) ja cos−1(x). Tässä merkintätavassa on kuitenkin vaarana, että käänteisfunktion sijasta sama merkintä voi tarkoittaa myös funktion negatiivista potenssia. Tämän välttämiseksi käytetään nimiä arcsin, arccos jne. trigonometristen funktioiden käänteisfunktioille.
Sovelluksia[muokkaa | muokkaa wikitekstiä]
Trigonometriset funktiot ovat, kuten nimestäkin käy ilmi, ratkaisevan tärkeitä trigonometriassa. Tämä johtuu pääasiassa kahdesta seuraavasta kaavasta:
Sinilause[muokkaa | muokkaa wikitekstiä]
Sinilauseen mukaan mille tahansa kolmiolle pätee:
joka voidaan esittää myös muodossa

jossa a, b ja c ovat kolmion sivut, α on sivun a vastainen kulma, β on b:n vastainen kulma, γ on c:n vastainen kulma ja R on kolmion ympäri piirretyn ympyrän säde. Sinilause voidaan todistaa jakamalla kolmio kahteen suorakulmaiseen kolmioon ja käyttämällä yllä esitettyä sinin määritelmää suorakulmaisen kolmion sivujen suhteina. Sinilause on hyödyllinen laskettaessa tuntemattomien sivujen pituuksia, kun kaksi kulmaa ja yksi sivu on tiedossa. Tämä on yleinen tilanne kolmioinnissa, jonka avulla mitataan tuntemattomia pituuksia määrittämällä kaksi kulmaa ja niiden välinen pituus.
Kosinilause[muokkaa | muokkaa wikitekstiä]
Kosinilause on Pythagoraan lauseen laajennus mielivaltaisille kolmioille:
joka voidaan muotoilla myös
jossa a, b ja c ovat kolmion sivut ja γ on sivun c vastainen kulma. Tämänkin lauseen todistus on yksinkertainen kun jaetaan tutkittava kolmio kahteen suorakulmaiseen kolmioon. Kosinilauseen avulla voidaan laskea kolmion puuttuvat tiedot jos kaksi sivua ja kulma on tiedossa.
Kannattaa huomata että kolmio ei välttämättä ole yksikäsitteisesti määrätty, jos tunnettu kulma ei sijaitse tunnettujen sivujen välissä. Tällöin kosinilauseen ratkaisussa saadaan kaksi vaihtoehtoista sivun pituutta.
Tangenttilause[muokkaa | muokkaa wikitekstiä]
On olemassa myös tangenttilause:
jossa a ja b kolmion sivuja, ja α ja β ovat niitä vastaavat kulmat.
Trigonometriset funktiot ovat tärkeitä muissakin kohteissa kuin kolmioiden tutkimuksessa. Ne ovat jaksollisia funktioita, joiden kuvaajille ominainen aaltomuoto on hyödyllinen toistuvien ilmiöiden, kuten ääni- ja valoaaltojen mallintamisessa. Jokainen signaali voidaan kirjoittaa eritaajuisten sinifunktioiden (tavallisesti äärettömänä) summana; tämä on perustavanlaatuinen ajatus harmonisessa analyysissä, jossa trigonometrisia sarjoja käytetään osittaisdifferentiaaliyhtälöiden erilaisten reuna-arvotehtävien ratkaisussa.
Katso myös[muokkaa | muokkaa wikitekstiä]
Lähteet[muokkaa | muokkaa wikitekstiä]
- ↑ Trigonometric function Encyclopedia Britannica. 9.12.2022. Viitattu 17.1.2023. (englanniksi)
- ↑ Nevanlinna, R., Paatero, V.: ”VI”, Funktioteoria, s. 89. Helsinki: Otavan korkeakoulukirjasto, 1971.
- ↑ Nevanlinna, R., Paatero, V.: ”VI”, Funktioteoria, s. 94. Helsinki: Otavan korkeakoulukirjasto, 1971.
- ↑ Nevanlinna, R., Paatero, V.: ”VI”, Funktioteoria, s. 93. Helsinki: Otavan korkeakoulukirjasto, 1971.
- ↑ Lauri Myrberg: ”Trigonometriset funktiot”, DIfferentiaali- ja integraalilaskenta, osa 1, s. 86. Kirjayhtymä, 1977. ISBN 951-26-0936-3.
- ↑ Lauri Myrberg: ”Täydennys trigonometrisiin funktioihin”, DIfferentiaali- ja integraalilaskenta, osa 1, s. 161-162. Kirjayhtymä, 1977. ISBN 951-26-0936-3.
- ↑ Lauri Myrberg: ”Trigonometristen funktioiden derivaatat”, Differentiaali- ja integraalilaskenta, osa 1, s. 112. Kirjayhtymä, 1977. ISBN 951-26-0936-3.
- ↑ a b Lauri Myrberg: ”Täydennys trigonometrisiin funktioihin”, Differentiaali- ja integraalilaskenta, osa 2, s. 133-136. Kirjayhtymä, 1977. ISBN 951-26-0936-3.
Kirjallisuutta[muokkaa | muokkaa wikitekstiä]
- Rikkonen, Harri: Matematiikan pitkä peruskurssi II – Reaalimuuttujan funktioiden differentiaalilasku. Helsinki: Otakustantamo, 1969. ISBN 951-671-022-0.
- Pitkäranta, Juhani: Calculus Fennicus – TKK:n 1. lukuvuoden laaja matematiikka (2000–2013) (pdf) Helsinki: Avoimet oppimateriaalit ry. ISBN 978-952-7010-12-9 ISBN 978-952-7010-6 (pdf).
Aiheesta muualla[muokkaa | muokkaa wikitekstiä]






























































![{\displaystyle \lim _{\theta \to 0}\left[{\frac {\sin {\theta }}{\theta }}\cdot {\frac {\sin {\theta }}{(1+\cos {\theta })}}\right]=\lim _{\theta \to 0}{\frac {\sin {\theta }}{\theta }}\cdot \lim _{\theta \to 0}{\frac {\sin {\theta }}{(1+\cos {\theta })}}=1\cdot 0=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d25cad50839eedde5af3530d0b58ea38a07fe12e)






























































![{\displaystyle \lim _{h\to 0}\left[\sin {x}\cdot {\cfrac {\cos {h}-1}{h}}+\cos {x}\cdot {\cfrac {\sin {h}}{h}}\right]=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/150e781ca93b5af21e1fd865d036981f10e52959)








![{\displaystyle {\frac {a+b}{a-b}}={\frac {\tan[{\frac {1}{2}}(\alpha +\beta )]}{\tan[{\frac {1}{2}}(\alpha -\beta )]}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e4a8f253e02afa67bcc9b6073fec1ce8bca2496)
