Erityinen suhteellisuusteoria
Suppea suhteellisuusteoria eli erityinen suhteellisuusteoria tai erikoinen suhteellisuusteoria on fysiikassa yleisesti hyväksytty ja kokeellisesti hyvin tuettu tieteellinen teoria, jonka Albert Einstein julkaisi 1905. Se korvasi newtonilaisen eli klassisen mekaniikan käsityksen muuttumattomasta avaruudesta ja ajasta näiden yhtymäksi, aika-avaruudeksi, ja sisällytti itseensä sähkömagnetismin teorian, kuten Maxwellin yhtälöissä on esitetty.
Muuttumattomalla nopeudella liikkuvan kappaleen sanotaan olevan inertiaalikoordinaatistossa. Jos vakionopeuksisia kappaleita on monia ja ne liikkuvat samaan suuntaan, ovat ne samassa inertiaalikoordinaatistossa. Jos inertiaalikoordinaatistoja on monia, ovat niiden kappaleiden ominaisuudet suhteellisia toisiinsa, ja ominaisuuksia voidaan verrata suppean suhteellisuusteorian avulla, josta nimi suhteellisuusteoria tulee. Teoria on suppea, koska se pätee vain inertiaalikoordinaatistoille, eikä siinä voi siten suhteellistaa kiihtyviä tai hidastuvia liiketiloja.[1] Suppeassa suhteellisuusteoriassa jätetään huomiotta kappaleiden painovoiman luonne, joka yleisen suhteellisuusteorian mukaan aiheuttaa aika-avaruuden vääristymistä ja kaikki liike, myös kiihtyvä, on saatettu teoriassa silloin yleisesti suhteellistetuksi.
Suppeassa suhteellisuusteoriassa vertaillaan inertiaalikoordinaatistojen kappaleiden ominaisuuksia, kuten suhteellista sijaintia, nopeutta ja liike-energiaa, Lorentz-muunnoksilla. Nämä ottavat huomioon aika-avaruuden muuttumisen, joka on merkittävää eritoten tyhjiön valonnopeutta lähellä olevissa suhteellisissa nopeuksissa. Klassisessa mekaniikassa käytetään samankaltaisia Galilei-muunnoksia, jotka eivät ota huomioon aika-avaruuden muutoksia.[1] Klassista mekaniikkaa voidaan pitää siksi nykyään enää vain suhteellisuusteorian approksimaationa, jota voidaan soveltaa valoa paljon hitaammissa nopeuksissa.
Suppean suhteellisuusteorian pääkohdat julkaistiin 1905 Annalen der Physik -tiedejulkaisun numerossa 10 Einsteinin artikkelissa Liikkuvien kappaleiden elektrodynamiikasta (saks. zur elektrodynamik bewegter körper).[2] Samassa numerossa julkaistiin myös Einsteinin valokvantteja ja Brownin liikettä käsitelleet artikkelit.
Suppeasta suhteellisuusteoriasta seuraa myös massan ja energian välisen yhteyden osoittava yhtälö E=mc². Yhtälö julkaistiin myöhemmin 1905 Einsteinin kirjoittamassa Annalen der Physikin artikkelissa Riippuuko kappaleen hitaus sen energiasta? (saks. Ist die trägheit eines körpers von dessen energieinhalt abhängig?).[3]
1915 Einstein julkaisi toistaiseksi epävarman yleisen suhteellisuusteorian. Se on suppean suhteellisuusteorian yleispätevämpi laajennos, josta teorian nimi yleinen johtuu. Teorian avulla voidaan tarkastella muun muassa kiihtyvää tai hidastuvaa liikettä, painovoimaa, mustia aukkoja, aika-avaruuden kaareutumista ja maailmankaikkeuden kehitystä.[1]
Postulaatit[muokkaa | muokkaa wikitekstiä]
- Suhteellisuusperiaate: Fysiikan lait ovat samat jokaisessa inertiaalikoordinaatistossa.[4] Avaruudessa ei siis ole mitään toisia parempaa erityispistettä tai suuntaa, jonka voisi määrätä olevan paikallaan tai nopeudeltaan nolla.
- Valon (tai muun sähkömagneettisen säteilyn) tyhjiönopeus on sama kaikissa inertiaalikoordinaatistossa, eikä riipu valon lähteen ja havaitsijan keskinäisestä nopeudesta.[4]
Postulaatit ovat olettamuksia, joihin suppea suhteellisuusteoria perustuu. Postulaateista toinen on seuraus ensimmäisestä.[1]
Suhteellisuusteorian seurauksia[muokkaa | muokkaa wikitekstiä]
Postulaateista seuraa suppean suhteellisuusteorian mukaan muun muassa seuraavanlaisia maailmankaikkeuden ominaisuuksia:
- Levossa olevalle samanaikaiset tapahtumat eivät ole samanaikaisia kuin levossa olevan kannalta liikkeessä olevalle.
- Ajankulku on suhteellista ja suhteellisesti liikkuvan aika kuluu hitaammin (katso kaksosparadoksi). Siten ajassa eteenpäin "matkustaminen" on mahdollista.
- Levossa olevan suhteen liikkuvien kappaleiden kulkema matka on fyysisesti lyhempi kuin levossa olevan mittaamana ja levossa olevan mittaamana liikkuvat kappaleet lyhentyvät/litistyvät menosuuntaansa. Esimerkiksi raketin lähtiessä Maasta ja liikkuessa lähes valonnopeudella suhteessa Maahan, on raketti Maasta mitattuna fyysisesti lyhentynyt pitkittäin menosuuntaansa. Raketista katsoen Maa ja muu Maan kaltaisella nopeudella liikkuva universumi on litistynyt raketin menosuuntaan. Siten myös raketin kannalta sen kulkema matka on lyhyempi kuin maasta mitattuna. (Katso myös: Tikapuuparadoksi.)
- Aine voi muuntua energiaksi ja päinvastoin, rikkoen massan säilymislain. Tätä tapahtuu havaittavasti ydinreaktioissa, mutta jatkuvasti myös arkielämässä, joskin tämä on huomaamattomampaa.
- Sähkömagneettinen säteily liikkuu tyhjiössä aina valonnopeudella havaitsijasta riippumatta. Esimerkiksi suhteessa Maahan lähellä valonnopeutta liikkuvan raketin matkustajat näkevät valon liikkuvan tyhjiössä edelleen valonnopeudella huolimatta heidän rakettinsa nopeudesta. Maasta raketin rinnalle lähetetty lasersäde ei siis raketista mitattuna liiku hitaammin kuin Maasta mitattuna.
- Massallinen kappale ei voi saavuttaa tyhjiön valonnopeutta suhteessa levossa olevaan kappaleeseen sillä massallinen kappale vaatii valonnopeuden saavuttamiseksi äärettömästi energiaa. Massallinen tai massaton hiukkanen valonnopeuden ylittäessään jossakin inertiaalikoordinaatistossa rikkoisi myös syy-seuraus suhteen (kausaliteetin). Tällöin tapahtuman A aiheuttama tapahtuma B, jota valoa nopeampi kappale välittää, ja joiden välillä on jokin etäisyys, voisi tapahtua ennen A:ta jossakin toisessa inertiaalikoordinaatistossa.
Saattaa kuulla väitettävän että suppean suhteellisuusteorian mukaan kaikki on suhteellista. Tämä ei pidä paikkaansa: muun muassa sähkömagneettisen säteilyn tyhjiönopeus, massan lepoenergia ja aika-avaruusintervalli (matemaattinen käsite) ovat kaikille havaitsijoille samat.
Inertiaalikoordinaatistot[muokkaa | muokkaa wikitekstiä]
Inertiaalikoordinaatistot ovat olennainen osa suppeaa suhteellisuusteoriaa.
Täysin muuttumattomalla nopeudella liikkuvan kappaleen sanotaan olevan inertiaalikoordinaatistossa. Jos vakionopeuksisia kappaleita on useita ja ne liikkuvat täysin samaan suuntaan, ovat ne samassa inertiaalikoordinaatistossa, vaikka kappaleiden välinen etäisyys olisi ääretön. Siten inertiaalikoordinaatistotkin ovat äärettömiä. Eri vakionopeudella tai eri suuntaan liikkuvat kappaleet ovat eri inertiaalikoordinaatistoissa. Inertiaalikoordinaatistot ovat ihanteellisia eli kuvitteellisia, eikä niitä oikeasti ole. Tämä johtuu siitä, että kaikkialla kappaleiden liikkeeseen vaikuttaa kaukaistenkin kappaleiden painovoima, jolloin minkään todellisen kappaleen nopeus ei voi olla täysin muuttumaton. Syvällä avaruudessa kaukana muista kappaleista oleva ja siten lähes vakionopeuksinen kappale on kuitenkin lähellä inertiaalikoordinaatistossa olevaa kappaletta.[1]
Kahden samaan suuntaan nopeudella 50 km/h liikkuvan auton voidaan sanoa olevan likimain samassa inertiaalikoordinaatistossa, ja 60 km/h samaan suuntaan menevä auto on omassaan. Nopeudet ovat aina kuitenkin suhteellisia. 50 km/h autojen voidaan sanoa olevan paikallaan koordinaatistossaan ja 60 km/h auton liikkuvan suhteessa näihin vain nopeudella 10 km/h. Todellista nopeutta etsiessä voidaan lähteä autoja vertaamaan niiden liikkeeseen suhteessa maapallon pintaan. Kuitenkin näiden maapallolla olevien autojen nopeutta voidaan myös verrata suhteessa Aurinkoon maapallon pyöriessä sen ympäri, sitten autojen liikettä suhteessa Linnunrataan aurinkokunnan liikkuessa sen halki ja niin edelleen.
Todellista nopeutta ei siis ole olemassa ja kaikki nopeudet ovat suhteellisia sekä suhteellisuusteoriassa että klassisessa mekaniikassa, joissa molemmissa nopeus on suuntaa huomioimatta kuljettu matkan muutos Δx jaettuna ajan muutoksella Δt, joissa Δ on muutosta merkitsevä matemaattinen symboli. Matka täytyy aina suhteuttaa johonkin, mitä varten on luotu koordinaatistojen käsite. Saman inertiaalikoordinaatiston kappaleet eivät liiku suhteessa toisiinsa, eli ne ovat toisiinsa nähden levossa, mutta liikkuvat suhteessa toisiin koordinaatistoihin. Minkään koordinaatiston ei kuitenkaan voida sanoa olevan levossa, vain liikkeessä suhteessa toisiinsa.[1]
Teorian synty[muokkaa | muokkaa wikitekstiä]
Suhteellisuus ei ole klassiselle fysiikalle vieras käsite. Newtonilaisessa mekaniikassa käytetään Galilei-invarianssin eli -muunnoksen kaavoja vertailemaan eri inertiaalikoordinaatistojen kappaleiden suhteellisia ominaisuuksia. Kaavoissa kuitenkin ajan, kuten matkaan käytetyn ajan, ja avaruuden, kuten kuljetun matkan, oletetaan olevan kaikissa koordinaatistoissa muuttumattomia eri koordinaatistojen kappaleiden välisissä nopeuksissa.[1]
Valon tiedettiin liikkuvan tyhjiössä valonnopeudella jo pitkään ennen Einsteinin suppeaa suhteellisuusteoriaa. 1865 James Maxwellin sähkömagnetismin teoria ennusti valon olevan sähkömagneettinen aalto, ja ennusti tyhjiön permittiivisyyden ε0 ja tyhjiön permeabiliteetin µ0 avulla valonnopeuden c olevan tyhjiössä[5]
Yhtälössä ei ole paikkaa ulkoisille muuttujille, jotka ottaisivat huomioon valon liikkeen eri inertiaalikoordinaatistoissa. Galilei-muunnoksen mukaan esimerkiksi nopeammassa liikkeessä olevan koordinaatiston kappaleen lähettäessä valoa, tulisi tämän valon liikkua nopeammin kuin hitaammassa liikkeessä olevan koordinaatiston kappaleen lähettämä valo. Tämän uskottiin pitävän paikkansa ennen suppeaa suhteellisuusteoriaa.[1]
Yllä oleva sähkömagnetismin kaava ei siis ole yhteensopiva klassisen mekaniikassa käytetyn Galilei-muunnoksen kanssa, koska kaava ennustaa valon tyhjiönopeuden olevan vakio ja koordinaatistosta riippumatta todennäköisesti sama. Ongelman ratkaisemiseksi ehdotettiin valoeetteriteoriaa. Arveltiin että valo liikkuu tyhjiössä valonnopeudella vain suhteessa universumin täyttävän, eetteriksi nimetyn asian muodostamaan koordinaatistoon, jonka suhteen sähkömagnetismin yhtälöt pätevät. Siten tyhjiön valonnopeus olisi myös pienempi eetterin suhteen liikkuvassa galileisessa koordinaatistossa: jos koordinaatisto liikkuu samaan suuntaan nopeudella v kuin valo suhteessa eetterikoordinaatistoon, olisi mitattu tyhjiön valonnopeus c - v. Tämä on arkijärjen mukaista.[1]
Olisi sittenkin siis olemassa muita parempi koordinaatisto, jonka suhteen voitaisiin mitata muiden koordinaatistojen kappaleiden todellinen nopeus. Jos eetteriä ei olisi, olisi klassinen mekaniikka, joka oli tuolloin valtavirran käsitys fysiikasta, ainakin osittain väärässä.[6]

Ennen 1800-luvun loppua ei onnistuttu tarkimmillakaan laitteilla mittaamaan valon ja liikkeessä olevan kappaleen välillä olevaa pientä eroa, jolla eetteriteoria voitaisiin todistaa. 1881 keksittiin käyttää interferometriä ja Maan nopeaa liikettä niin sanotun eetterituulen havaitsemiseksi, joka muodostuisi Maan ja muun aurinkokunnan liikkuessa maailmankaikkeuden sisältämän eetterin halki. Koe tunnetaan Michelsonin–Morleyn kokeena, ja sillä olisi havaittu pienikin ero eetterin ja Maan liikkeen välillä. Tässä kokeessa eikä muissakaan kokeissa kuitenkaan havaittu eetteriä, joten ei voitu määrittää missä sen koordinaatisto oli.[1]

Eetteriä ei siis vaikuttanut olevan, mutta muun tuon ajan fysiikkaan yhteensopimattomasta sähkömagnetismista sen sijaan oli todisteita. Tämä oli ongelmallista koska sähkömagnetismin avulla kuvattuna valo on sähkömagneettinen aalto, joka ylläpitää itseään vaihtelevasti muuttuvan sähkökentän ja magneettikentän avulla. Jos joku liikkuisi tyhjiön valonnopeudella valon mukana, ei hän havaitsisi kenttien muuttuvan ja siten valon ei myöskään pitäisi pystyä ylläpitämään itseään ilman eetteriä. Tämä johti Einsteinin tekemään suhteellisuusperiaatteeksi kutsutun johtopäätöksen, jonka mukaan[1]
- "Kaikki fysiikan lait ovat samat kaikissa inertiaalikoordinaatistoissa."
Tämä on suppean suhteellisuusteorian ensimmäinen postulaatti, joka kieltää eetterin olemassaolon. Postulaatista on johdettu koko suppea suhteellisuusteoria, myös sen toinen postulaatti. Väittämä vaikuttaa ongelmattomalta, mutta ei ole. Jos Maxwellin sähkömagnetismin teorian yhtälöitä pidetään fysiikan lakeina, kuten ne kokeiden mukaan tuolloin ja nyt näyttävät olevan, myös niiden tulisi päteä inertiaalikoordinaatistoissa. Einsteinin suhteellisuusperiaatteesta voidaan johtaa kolmivaiheinen johtopäätös:[1]
- Maxwellin yhtälöt pätevät kaikissa inertiaalikoordinaatistoissa.
- Maxwellin yhtälöt ennustavat tyhjiön valonnopeudeksi c ≈ 3 · 108 m/s.
- Tyhjiön valonnopeus c on kaikissa inertiaalikoordinaatistoissa sama.
Päätelmistä kolmas on suppean suhteellisuusteorian toinen postulaatti.[1]
Tämä tarkoittaa sitä, että jos joku liikkuu nopeudella 0,5 c (50 % tyhjiön valonnopeudesta) ja hänen menosuunnastaan sekä takaansa lähetetään kohtisuoraan valoa, ei suhteellisuusperiaatteen mukaan valo liikkuvasta näytä tulevan hänen edestään nopeudella 1,5 c = 1 c + 0,5 c ja takaansa nopeudella 0,5 c = 1 c - 0,5 c. Valo tulee liikkuvan näkökannalta samalla nopeudella 1 c molemmista suunnista, mikä vaikuttaa järjenvastaiselta. Asia on kuitenkin todistettu kokeellisesti 1905 esitetyn suhteellisuusteorian jälkeen muun muassa[1] jo 1932. Tällöin R. Kennedy ja E. Thorndike mittasivat merkittävää eroa havaitsematta valonnopeutta maapallolla eri kuukausina, jolloin mittauspaikka maapallolla liikkui Maan pyörimissuunnan vuoksi eri nopeuksilla suhteessa Aurinkoon.[7]
Kyse ei siis ole vain näkökannasta vaan valo todellakin liikkuu kaikissa inertiaalikoordinaatistoissa samalla nopeudella eli tyhjiön valonnopeudella.[1]
Tämä johtaa toiseen johtopäätökseen inertiaalikoordinaatistojen ajan suhteellisuudesta. Jos paikallaan seisova ja vakionopeudella kävelevä mittaavat vakionopeudella juoksevan henkilön nopeutta tämän juostessa pisteestä A pisteeseen B, on kävelijän oman inertiaalikoordinaatistonsa perusteella mittaama juoksijan nopeus väistämättä pienempi kuin seisojan, jos kävelijä menee samaan suuntaan kuin juoksija. Tietyssä ajassa juoksijan liikkuma matka on myös lyhyempi kuin seisojan näkökannalta koska kävelijä itsekin lähestyy pistettä B, eli piste B näyttää kävelijästä lähestyvän häntä. Tällaisissa tyhjiön valonnopeuteen verrattuna hitaissa nopeuksissa saadaan seisojan, kävelijän ja juoksijan havaitsemat muiden henkilöiden ja pisteiden nopeudet muunnettua ongelmitta toisikseen Galilei-muunnoksella.[1]
Jos juoksijan sijaan mitataan valon nopeutta pisteestä A pisteeseen B, tulee näennäinen ongelma. Suhteellisuusperiaatteen vuoksi tyhjiön valonnopeus on sama kussakin inertiaalikoordinaatistossa. Myös seisojan ja juoksijan mittaamat valon kulkemat matkat ovat eri. Nopeuden määritelmä on matka jaettuna ajalla, joten aika on nopeuden kaavassa ainoa jäljelle jäävä muuttuja.[1]
Ainoa johtopäätös on se, että aika ei ole muuttumaton eli absoluuttinen. Siten se on sijaintia mittaavien x-, y-, z-avaruuskoordinaattien mukaisesti neljäs koordinaatti, jota täytyy käyttää inertiaalikoordinaatistojen vertailuun. Suhteellisuusteorian mukaan aika on siksi kolmen tilaulottuvuuden lisäksi neljäs ulottuvuus. Yhdessä näitä kutsutaan aika-avaruuskoordinaateiksi.[1] Siksi puhutaan myös aika-avaruudesta, eikä ajasta ja avaruudesta, koska käsitteet ovat toisistaan riippuvaisia: myös avaruus on suppean suhteellisuusteorian mukaan muuttuva.
Suhteellisuusteoriassa aika-avaruuden muutoksen ottavat huomioon toisiinsa suhteellisina ajan ja avaruuden koordinaatteina Lorentz-muunnokset.[1]
Samanaikaisuuden suhteellisuus[muokkaa | muokkaa wikitekstiä]
Suppean suhteellisuusteorian mukaan aika on suhteellista, eikä se ole kaikissa inertiaalikoordinaatistoissa sama. Siksi myös yhdessä inertiaalikoordinaatistossa havaitut samanaikaiset tapahtumat eivät koskaan ole täysin samanaikaisia jossakin toisessa inertiaalikoordinaatistossa.[1]
Einstein esitti tämän havainnollistamiseksi ajatuskokeen junavaunulla, joka on suunnilleen seuraavanlainen. Junavaunun molemmissa päissä on räjähde. Vaunun keskellä ja täysin samoilla etäisyyksillä räjähteistä on Jaana, jolla on räjähdysten valonvälähdyksen havaitseva laite. Laitteessa on merkkivalo, johon syttyy pysyvästi punainen valo, jos se havaitsee välähdyksen tulevan ensin junan menosuunnasta, ja vihreä valo, jos välähdys tulee molemmilta suunnilta samanaikaisesti. Junaradan vieressä seisoo Simo, jonka ohi junavaunu liikkuu vakionopeudella.[1]
Ennen koetta Jaana ja Simo sopivat Simon räjäyttävän räjähteet samanaikaisesti kun Jaana ja Simo ovat kohdakkain junan liikkuessa Simon ohitse. Paikallaan seisova Simo olettaa siksi näkevänsä räjähdykset samaan aikaan ja laitteen valon muuntuvan punaiseksi, koska junassa oleva Jaana ehtii laitteineen siirtyä valon yhä liikkuessa sen verran eteenpäin että valo ehtii laitteelle ensin vain junan menosuunnasta.[1]
Jaana on kuullut suhteellisuusteorian suhteellisuusperiaatteesta, jonka mukaan valo liikkuu kaikkien havaitsijoiden mukaan aina samalla nopeudella riippumatta heidän nopeudestaan suhteessa johonkuhun toiseen paikallaan seisovaan, kuten Simoon. Jaana olettaa siksi näkevänsä räjähdykset täysin samanaikaisesti. Siten niistä tuleva valon pitäisi tulla laitteeseen molemmista suunnista samanaikaisesti, ja valon muuttua vihreäksi. Vaunun pysähtyessä ja tuloksia vertailtaessa Simo ei voi nähdä punaista valoa ja Jaana vihreää valoa samanaikaisesti.[1]
Kun koe suoritetaan käytännössä, valo muuttuu punaiseksi. Tämä johtuu siitä, että vaikka valonnopeus on molemmille havaitsijoille sama suhteellisuusperiaatteen mukaan, ei vaunussa oleva Jaana havaitsekaan räjähdyksiä samanaikaisesti toisin kuin hän oletti. Hän näkee räjähdyksen ensin menosuunnastaan ja vasta sitten tulosuunnastaan.[1]
Molemmat havaitsijat ovat kuitenkin oikeassa räjähdysten samanaikaisuudesta. Kyse ei ole vain havaitsemisesta, vaan räjähdykset tapahtuvat Jaanan inertiaalikoordinaatistossa (junassa) eri aikaan kuin Simon inertiaalikoordinaatistossa (junaradan vieressä).[1]
Aikavenymä ja tosiaika[muokkaa | muokkaa wikitekstiä]
- Katso myös: Kaksosparadoksi
Suppean suhteellisuusteorian mukaan kahden eri inertiaalikoordinaatiston ajankulku on eri. Tämän vuoksi koordinaatistoista katsottuna kahden eri aikaan tapahtuvan tapahtuman väliset aikaerot eivät ole samat ja tapahtuu aikavenymä eli aikadilataatio eli aikadilaatio. Kappale, jonka kohdalla tapahtumat tapahtuvat samassa pisteessä kuin kappale itsekin on, kuluu näiden tapahtumien välillä aika, jota kutsutaan tosiajaksi (eng. proper time), jota Einstein nimitti oma-ajaksi (saks. eigenzeit).[6]
Kaksi tapahtumaa voivat olla mitä tahansa, kuten lähteminen planeetalta ja saapuminen toiselle planeetalle raketilla. Raketti mittaa tosiaikaa koska lähtö ja saapuminen raketista katsoen samassa pisteessä: raketista katsoen lähtöplaneetta etääntyy raketin lähtiessä ja tuloplaneetta lähestyy raketin pysyessä paikoillaan omassa koordinaatistossaan.[1]
Kahden inertiaalikoordinaatiston välillä tapahtuva aikavenymän kaava on[1]
- Δt on kulunut aika eli ajan (t) muutos (Δ) inertiaalikoordinaatiston kappaleella, joka ei ole samoissa pisteissä kuin kaksi tapahtumaa. Δt on aikasamoissa yksiköissä kuin Δτ.
- Δτ on kulunut tosiaika kappaleella, joka on samoissa pisteissä kuin kaksi tapahtumaa. Δτ on samoissa aikayksiköissä kuin Δt.
- β on tosiaikaa mittaavan kappaleen nopeus v, joka on mitattu Δt mittaavasta inertiaalikoordinaatistosta katsottuna tyhjiön valonnopeuden c suhdeluku v/c, jonka arvo on välillä 0–1 eli 10 % tyhjiön valonnopeudesta on 0,1 ja 100 % tyhjiön valonnopeudesta on 1.
Esimerkkejä[muokkaa | muokkaa wikitekstiä]
Raketti liikkuu 90 % valonnopeudesta Maasta Marsiin Marsin ollessa lähimmillään Maata eli 5,5 · 1010 metrin matkan. Kuinka kauan matka kestää Maasta mitattuna ja raketista mitattuna?
- Maapallolla kulunut aika raketin lähdöstä sen saapumiseen saadaan nopeuden kaavalla
- Käyttäen edellä laskettua aikaa, on raketissa kulunut tosiaika raketin lähdöstä sen saapumiseen
- Maassa kuluu 3 minuuttia ja 24 sekuntia raketin matkaan. Raketin matkustajien mukaan matka kestää vain 1 minuutin ja 29 sekuntia. Todellisuudessa 0,9 c nopeuden saavuttamiseen ja vastaavasti hidastamiseen voi kulua useita kuukausia ilman että raketin matkustajat rusentuvat kiihdyttämisen aiheuttavien G-voimien vuoksi, jolloin raketti on perillä paljon ennen 0,9 c nopeuden saavuttamista. Raketin kiihtyvä liike aiheuttaa silti eron raketissa ja maassa mitatuissa ajoissa, mutta tätä ei voida laskea yhtä suoraviivaisesti.
Kaavan johtaminen[muokkaa | muokkaa wikitekstiä]
Aikavenymän kaava voidaan johtaa ajatuskokeellisella valokellolla, jossa on kaksi peiliä toisistaan korkeudella L tyhjiön erottamana, joiden välissä on edestakaisin heijastuva ja laitteesta häviämätön fotoni. Kello havaitsee fotonin heijastumisen alemmasta peilistä, jolloin kellon viisari liikahtaa aina yhden pykälän eteenpäin mitaten siten aikaa.[1]
Fotonin täytyy kahden viisarin liikkeen välissä edetä matka 2L, sillä se liikkuu alemmasta peilistä matkan L ylempään peiliin ja takaisin, eli kaksinkertaisen matkan. Fotoni liikkuu tyhjiön valonnopeudella c, joten viisarin liikkeiden välissä kulunut aika on Δt = 2L/c.[1]
Suhteellisuusperiaatteen mukaan valo liikkuu kaikissa inertiaalikoordinaatistoissa näissä olevien havainnoijien mittaamana tyhjiön valonnopeudella. Siksi kellon liikkuessa jostakin havainnoitsijasta sivuttain muuttumattomalla ja valoa hitaammalla nopeudella v fotonin ylös-alas etenevään liikkeeseen nähden, on fotonin kulkema matka alapeililtä yläpeilille kellon suhteen mukana liikkumattomalle suurempi kuin kellon mukana liikkuvan havaitsema liike.[1]

Suhteellisuusperiaatteen vuoksi kellon mukana liikkuva näkee fotonin liikkuvan suoraan ylös ja alas tyhjiön valonnopeudella eli se kulkee matkan ajassa Δt = 2L/c.[1]

Suhteellisuusperiaatteen vuoksi kellon mukana liikkumaton näkee fotonin liikkuvan siksaksakkia peilien välissä tyhjiön valonnopeudella valokellon peilien siirtyessä hänestä poispäin. Havaitsijan mukaan fotonilta kuluu aikaa Δt' verran kuljettuaan alapeililtä yläpeilille ja takaisin. Matkaan alapeililtä yläpeilille kuluu siten puolet tästä ajasta eli ½Δt'. Koska nopeus on matka jaettuna ajalla, on fotonin liikkeen aikana alapeililtä yläpeilille liikkuma matka nopeus kertaa aika eli ½c Δt'. Kun fotoni alapeililtä tullessaan osuu yläpeiliin, on nopeudella v liikkuva valokello nopeuden kaavalla laskettuna siirtynyt matkan ½v Δt'.[1]

Valokellon mukana liikkumattoman havaitsijan mukaan fotoni on yläpeilille saapuessa muodostanut liikeradan, joka on suorakulmainen kolmio suhteessa peileihin. Kolmion hypotenuusan pituus on ½c Δt', viereinen kateetti on ½v Δt' ja vastainen kateetti on valokellon korkeus h. Kolmio on suorakulmainen, joten siihen pätee Pythagoraan lause ja tiedot voidaan esittää kaavana[1]
h2 + (½v Δt')2 = (½c Δt')2
Kun kaavasta ratkaistaan valokellon mukana liikkumattoman havaitsijan fotonin siksakkiliikkeeseensä kuluttama aika Δt' kahden viisarin liikkeen välillä, saadaan yhtälö[1]
Δt on 2L/c. Se on myös tosiaika Δτ, koska se on valokellon mukana liikkuvan havainnoima aika. β on kellon nopeuden ja tyhjiön valonnopeuden suhde v/c, joten v2/c2 on β2. Koska 2L/c = Δτ ja v2/c2 = β2, on lopullinen kaava[1]
Pituuspuristuma ja tosipituus[muokkaa | muokkaa wikitekstiä]
Johtuen suppean suhteellisuusteorian aikavenymästä, ei kahden pisteen välinen etäisyys ole sama kahdessa eri inertiaalikoordinaatistossa ja tapahtuu pituuspuristuma. Pisteiden ollessa toisessa inertiaalikoordinaatistossa paikallaan, kutsutaan näiden pisteiden välillä olevaa etäisyyttä tosipituudeksi (eng. proper length). Pisteiden välinen muutos inertiaalikoodrinaatistossa, josta nähden pisteet ovat liikkeessä, saadaan kaavalla[1]
- L on pisteiden välinen etäisyys inertiaalikoordinaatistosta mitattuna, jonka suhteen pisteet liikkuvat.
- l on tosipituus eli pisteiden välinen etäisyys inertiaalikoordinaatistosta mitattuna, jonka suhteen pisteet ovat paikallaan.
- β on tosiaikaa mittaavan kappaleen nopeus v, joka on mitattu Δt mittaavasta inertiaalikoordinaatistosta katsottuna tyhjiön valonnopeuden c suhdeluku v/c, jonka arvo on välillä 0–1 eli 10 % tyhjiön valonnopeudesta on 0,1 ja 100 % tyhjiön valonnopeudesta on 1.
Kaava pätee mille tahansa pisteille kuten kappaleiden kulkemille välimatkoille, mutta myös kaikille näiden kappaleiden itsensä pituudelle. Maasta laskettuna lähellä tyhjiön valonnopeutta liikkuvan raketin pituus on fyysisesti lyhempi kuin sen pituus, jos se olisi maahan nähden paikallaan.[1]
Pituuspuristuman kaava ei kerro kuitenkaan miltä raketti varsinaisesti näyttää silmin katsottuna.[1] Raketista tuleva valo näkyy aikavenymän vuoksi eri ajan hetkinä, jolloin raketin näkyvä muoto ja sijainti muuttuu. Myös raketista tulevan valon aallonpituus muuttuu raketin liikkeen vuoksi. Yhdessä näitä vaikutuksia kutsutaan suhteelliseksi Doppler-vaikutukseksi (eng. relativistic Doppler effect).

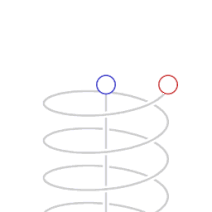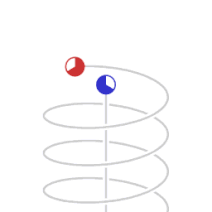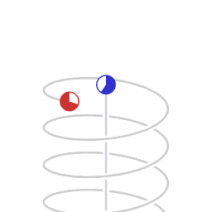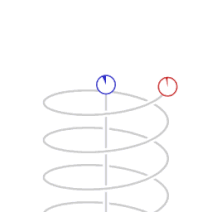
Yllä olevassa kuvassa pallo lähestyy havaitsijaa (sininen piste) tai pallon kannalta havaitsija lähestyy palloa hyvin suurella vakionopeudella kohtisuoraan. Pallo on fyysisesti puristunut ellipsoidiksi (harmaa) suhteessa havaitsijan koordinaatistoon. Havaitsija kuitenkin näkee ellipsoidin muuttavan muotoaan, väriään ja sijaintiaan suhteessa todelliseen sijaintiinsa, ja siten myös näkyvää nopeuttaan. Pallosta havaitsijalle tulevalle valolle tapahtuu sinisiirtymä eli sen aallonpituus on pienentynyt pallon tullessa kohti. Nopeudesta riippuen vihreä pallo voisi näyttää tällöin violetilta tai hyvin suurissa nopeuksissa olla näkymätön lähettäen silmille näkymätöntä gammasäteilyä. Pallon ohitettua havaitsijan tapahtuu punasiirtymä, aallonpituus kasvaa ja vihreä pallo voisi näkyä havaitsijalle punaisena tai hyvin suurissa nopeuksissa olla näkymätön lähettäen silmille näkymättömiä radioaaltoja.
Vasemmalla yllä animaatiossa näkyy miltä havaitsijasta (sininen piste) näyttäisi tunneli, jossa hän on, jos hän liikkuisi sen halki eri nopeuksilla. Animaatio alkaa havaitsijan ollessa levossa ja päättyy havaitsijan liikkuessa 70 % tyhjiön valonnopeudesta eli 0,7 c. Oikealla yllä on kuva tunnelista ulkoapäin 0,7 c nopeudessa, joka on tosin esitetty vain tunnelissa liikkuvan havaitsijan näkökulmasta: tunnelin suhteen paikallaan olevalle tunneli näyttää ulkoa tavalliselta. Tunnelissa liikkuvasta havaitsijasta seinämän muodot muuttuvat ja niistä tulevan sähkömagneettisen säteilyn kuten valon aallonpituus muuttuu: animaatiossa/kuvassa sininen on lyhyt aallonpituus, punainen on suuri aallonpituus.
Samaan tapaan avaruudessa matkaavasta tähdet näyttävät lähentyvän toisiaan ja todella lähellä tyhjiön valonnopeutta tähdet ovat matkaavasta hänen edessään yhtenä pisteenä, joka tosin ei näy silmin, sillä sen aallonpituus on lyhentynyt gammasäteilyksi.[8]
Esimerkkejä[muokkaa | muokkaa wikitekstiä]
Raketti liikkuu 90 % valonnopeudesta, Maasta Marsiin Marsin ollessa lähimmillään Maata eli 5,5 · 1010 metrin matkan. Kuinka pitkä välimatka on raketista mitattuna?
- Matka raketista mitattuna on
- Maassa olevien mittaama Maan ja Marsin välimatka on L' ja raketin matkaan kuluttama aika Δt'. Raketissa olevien välimatka on L ja matkaan kulunut aika Δt. Aikavenymä-osion esimerkissä maassa olevien mittaamana raketti kulki matkan noin 204 sekunnissa ja raketissa olevien mittaamana noin 89 sekunnissa. Maassa olevien mukaan raketti liikkuu nopeudella v, joka on 0,9 c. Raketissa olevien tulisi mitata nopeudekseen sama. Nopeus on matka jaettuna ajalla, joten kaava on v = L / Δt = L' / Δt'.
- L' / Δt' = (5,5 · 1010 m) / (204 s) ≈ 2,7 · 108 m/s ≈ 0,9 c.
- L / Δt = (2,4 · 1010 m) / (89 s) ≈ 2,7 · 108 m/s ≈ 0,9 c.
- Nopeudet ovat siis samat ja suppean suhteellisuusteorian kaavojen tulokset ovat järkeviä.
Kaavan johtaminen[muokkaa | muokkaa wikitekstiä]
Pisteiden välillä liikkuvan kappaleen inertiaalikoordinaatistosta mitattuna sen matkaan käyttämä aika Δt on lyhyempi kuin pisteisiin nähden paikallaan olevasta Δt' mittaavasta inertiaalikoordinaatistosta. Kappaleen nopeuden v kuitenkin täytyy olla molemmista koordinaatistoista laskettuna sama. Siten pisteiden välillä liikkuvan kappaleen kulkema matkan L tulee olla myös lyhyempi kuin pisteisiin nähden liikkumattomasta koordinaatistosta mitattu matka L'. Kaavana tämä on[1]
Δt on tosiaika Δτ, jonka kaava johdettiin aikavenymä-osiossa. Siten kaava on[1]
Δt' sulkee itsensä pois kaavasta ja saadaan pituuspuristuman kaava, jossa L' on tosipituus l[1]
Aika-avaruusintervalli[muokkaa | muokkaa wikitekstiä]
Suppeassa suhteellisuusteoriassa aika-avaruusintervalli s2 on kaikille inertiaalikoordinaatistoille sama. Se on matemaattinen käsite, jota voidaan käyttää vertailemaan eri inertiaalikoordinaatistojen välisiä tapahtumien etäisyyksiä ja aikoja toisiinsa mikäli niistä jo osa tiedetään. Aika-avaruusintervallin s2 kaava pelkkää etäisyyttä käyttäen (eikä kolmen tilaulottuvuuden x-, y- ja z-koordinaatteja) on[1]
- s2 on aika-avaruusintervalli, jonka yksikkö on neliömetri (m2).
- c on valonnopeus tyhjiössä eli tasan 299 792 458 m/s.
- Δt on tarkastellusta inertiaalikoordinaatistosta mitattu tapahtumien välinen aika.
- Δx on tarkastellusta inertiaalikoordinaatistosta mitattu tapahtumien välimatka.
Esimerkkejä[muokkaa | muokkaa wikitekstiä]
Pommi räjähtää ja 2 mikrosekunnin (µs) kuluttua tästä toinen pommi räjähtää 300 m päässä. Räjähdyksistä ohilentävä avaruusalus mittaa räjähdysten etäisyydeksi 200 m. Millä aikavälillä avaruuslentäjät havaitsevat räjähdykset?
- Valo liikkuu noin 300 m/µs, joten 2 µs se liikkuu 600 m ja intervalli on
- Lentäjille yhtälö on
- Ratkaistaessa yhtälöstä Δt', saadaan aikaväliksi Δt' = 1,85 µs.
Kaavan johtaminen[muokkaa | muokkaa wikitekstiä]

Kuvitellaan olevan xy-koordinaatisto ja tämän suhteen johonkin kulmaan käännetty x'y'-koordinaatisto. Koordinaatistojen asteikkovälit ovat samat. Päällekkäin ollessaan koordinaatistot voivat mitata koordinaatistoissa olevan viivan pituuden d sen toisessa päässä olevan pisteen 1 koordinaatteina ja toisessa päässä olevan pisteen 2 koordinaatteina. Koordinaatit eivät kuitenkaan ole pisteille samat eli x1 ≠ x1' jne. Intervalliksi kutsutaan esimerkiksi xy-koordinaatistossa arvojen x1 ja x2 välistä eroa Δx. Intervallitkaan koordinaatistojen välillä eivät ole samat, eli Δx ≠ Δx' ja Δy ≠ Δy'. Koordinaatistojen mittaama pituus d on kuitenkin sama. Kaavana tämä on[1]
Aikavenymä-osion valokellon kohdalla tyhjiön valonnopeuden lisäksi valokellon korkeus L on ainoa tekijä, joka on kellon mukana liikkuvalle ja kellon mukana liikkuvalle sama. Kaavana tämä on[1]
½ sulkevat toisensa pois ja kaava muuntuu muotoon[1]
Aika-avaruusintervalli on siten[1]
Ajan- ja paikanluontoinen intervalli[muokkaa | muokkaa wikitekstiä]
Kahden tapahtuman välinen aika-avaruusintervalli voi olla joko ajanluontoinen tai paikanluontoinen taikka rajatapauksessa valonluontoinen riippuen siitä, onko niiden tapahtumapaikkojen välinen etäisyys suurempi, pienempi vai yhtäsuuri kuin niiden välinen aikaero kerrottuna valonnopeudella. Tämä tapahtumaparin välisen intervallin luonne on sama kaikissa koordinaatistoissa.
Jos tapahtumapaikkojen välinen etäisyys Δx on pienempi kuin niiden välinen aikaero Δt kerrottuna valonnopeudella c eli Δx < cΔt, tapahtumien välinen intervalli on ajanluontoinen. Silloin intervalli , eli se on positiivinen ja sen neliöjuuri s positiivinen reaaliluku. Tämä edellyttää, että jompikumpi tapahtumista on sen verran toista varhaisempi, että varhaisemmasta tapahtumasta lähtenyt valo tai muu valonnopeudella etenevä signaali ehtii myöhemmän tapahtumapaikalle ennen itse tapahtumaa. Tässä tapauksessa edellinen tapahtuma on kaikissa koordinaatistoissa varhaisempi kuin jälkimmäinen. Tällöin on myös mahdollista, että varhaisempi tapahtuma vaikuttaa jälkimmäiseen, eli edellinen niistä on syy ja jälkimmäinen seuraus.
Jos sen sijaan tapahtumapaikkojen välinen etäisyys Δx on suurempi kuin niiden välinen aikaero Δt kerrottuna valonnopeudella c eli Δx > cΔt, tapahtumien välinen intervalli on paikanluontoinen. Silloin intervalli , eli se on negatiivinen ja sen neliöjuuri s imaginaariluku. Näin on laita, jos tapahtumat sattuvat niin kaukana ja niin lyhyen ajan kuluessa toisistaan, että kummastakaan lähtenyt valo ei ehdi toisen tapahtumapaikalle itse tapahtumaan mennessä. Esimerkiksi koska Auringosta valo tulee Maahan noin kahdeksassa minuutissa, kahden sellaisen tapahtuman välinen intervalli, joista toinen sattuu Maassa, toinen Auringossa vähemmän kuin kahdeksan minuuttia aikaisemmin tai myöhemmin, on paikanluontoinen. Tällöin tapahtumien aikajärjestyskään ei ole yksikäsitteinen, vaan tiettyyn suuntaan tarpeeksi nopeasti liikkuvan havaitsijan lepokoordinaatistossa se voi olla päinvastainen, ja on myös mahdollista valita koordinaatisto, jossa tapahtumat ovat samanaikaiset. Tällaisista tapahtumista kumpikaan ei voi olla toisen syy tai seuraus.
Rajatapauksessa tapahtumapaikkojen välinen etäisyys Δx on yhtä suuri kuin niiden välinen aikaero Δt. Tässä tapauksessa intervallia sanotaan valonluontoiseksi, sillä toisesta tapahtumasta lähtevä valonsäde saavuttaa toisen tapahtumapaikan juuri tapahtumahetkellä. Tällöin intervalli saa arvon nolla.
Liikemäärän suhteellisuus[muokkaa | muokkaa wikitekstiä]

Suppeassa suhteellisuusteoriassa inertiaalikoordinaatistossa olevan massallisen kappaleen liikemäärä eli momentti riippuu sen nopeudesta suhteessa toiseen inertiaalikoordinaatistoon. Klassisessa mekaniikassa massallisen kappaleen liikemäärä kasvaa lineaarisesti sen nopeuden kasvaessa, mutta suppeassa suhteellisuusteoriassa liikemäärä kasvaa kohti äärettömyyttä ja tyhjiön valonnopeudessa kappaleen liikemäärä on ääretön, jonka vuoksi massalliset kappaleet eivät voi liikkua valoa nopeammin.[1]
Suppeassa suhteellisuusteoriassa massallisen kappaleen eli partikkelin liikemäärä suhteessa johonkin inertiaalikoordinaatistoon on[1]
- p on suhteellinen liikemäärä yksiköissä Ns (newtonsekunti) eli kg · m/s.
- γp on yksikötön Lorentz-kerroin koordinaatiston partikkelille eikä sen koordinaatistolle, jota alaindeksin p merkitsee.
- m on kappaleen massa kilogrammoina.
- v on kappaleen suhteellinen nopeus yksiköissä m/s.
γp kaava suhteessa johonkin toiseen kuin tarkastellun kappaleen inertiaalikoordinaatistoon on[1]
- c on valonnopeus tyhjiössä eli tasan 299 792 458 m/s.
Esimerkkejä[muokkaa | muokkaa wikitekstiä]
Mikä on elektronin liikemäärä jos sen nopeus on 0,999 c suhteessa elektronin kiihdyttäneeseen hiukkaskiihdyttimeen?
- Lorentz-kerroin elektronille hiukkaskiihdyttimen inertiaalikoordinaatistosta laskettuna on
- Elektronin massa on noin 9,11 · 10-31 kg ja tyhjiön valonnopeus noin 3 · 108 m/s, joten liikemäärä on noin
- Elektronin todellinen liikemäärä on noin 22,37 kertaa suurempi kuin klassisen mekaniikan liikemäärän kaava p = mv ennustaa.
Energian suhteellisuus[muokkaa | muokkaa wikitekstiä]
Suppean suhteellisuusteorian mukaan massallisen kappaleen kokonaisenergia E jouleina (J) on[1]
- γp on yksikötön Lorentz-kerroin koordinaatiston partikkelille eikä sen koordinaatistolle, jota alaindeksin p merkitsee.
- m on kappaleen massa kilogrammoina.
- c on valonnopeus tyhjiössä eli tasan 299 792 458 m/s.
Kappaleen lepoenergia E0 jouleina on[1]
Kappaleen liike-energia eli kineettinen energia K jouleina on[1]
γp kaava suhteessa johonkin toiseen kuin tarkastellun kappaleen inertiaalikoordinaatistoon on[1]
Esimerkkejä[muokkaa | muokkaa wikitekstiä]
Mikä on elektronin lepo-, liike- ja kokonaisenergia jos sen nopeus on 0,999 c suhteessa sen kiihdyttäneeseen hiukkaskiihdyttimeen?
- Lorentz-kerroin elektronille hiukkaskiihdyttimen inertiaalikoordinaatistosta laskettuna on
- Elektronin massa on noin 9,11 · 10-31 kg ja tyhjiön valonnopeus noin 3 · 108 m/s, joten lepoenergia on noin
- Liike-energia on noin
- Kokonaisenergia on
Ydinreaktorissa uraanin isotooppi 235 absorboi neutronin ja fissioituu barium-141:ksi ja krypton-92:ksi, jolloin vapautuu 3 neutronia. 235U massa on 235,0439 g/mol, 141Ba 140,9144 g/mol, 92Kr 91,9262 g/mol ja neutronin 1,0087 g/mol. Paljonko moolista 235U vapautuu energiaa?
- Absorboitua neutronia ei tarvitse huomioida ja massavaje voidaan laskea suoraan 235U massalla 236U sijaan. Massavaje lasketaan vähentämällä 235U massasta reaktion tuotteiden massat. Saadaan
- Moolista energiaksi muuntunut massa on 0,0008228 kg. Valonnopeus tyhjiössä on noin 3 · 108 m/s. Lepomassan energian kaavalla vapautunut energia on noin
- Vapautuu noin 7,4 terajoulea energiaa. Fissio saattaa voida jatkua pidemmällekin, jolloin vapautuu enemmän energiaa. Fissio ei kuitenkaan käytännössä ole täydellistä ja muunlaisiakin ydinreaktioita voi tapahtua.
Kaavojen johtaminen[muokkaa | muokkaa wikitekstiä]
Aika-avaruusintervallin kaava johdettiin sen omassa osiossa. Aika-avaruusintervalli massallisen hiukkasen inertiaalikoordinaatistolle, joka liikkuu vakionopeudella ajassa Δt matkan Δx, on[1]
Hiukkanen liikkuu matkan suhteessa toiseen inertiaalikoordinaatistoon, josta käsin mitattuna tämän koordinaatiston kappaleet ovat levossa inertiaalikoordinaatiston määritelmän mukaisesti. Intervalli on invariantti, eli molemmille koordinaatistoille sama. Aika-avaruusintervallin kaava voidaan muuntaa liikemäärän p sisältäväksi yhtälöksi kertomalla yhtälö arvolla m / Δτ2, jossa Δτ on tosiaika, eli liikkuvan hiukkasen itsensä mittaama matkaansa käyttämä aika, joka ei aikavenymän vuoksi ole sama kuin Δt. Saadaan[1]
p = m(Δx/Δτ), joten yllä oleva kaava pätee. Δτ voidaan muuntaa Δt arvoksi ja päinvastoin Lorentz-kertoimella γp eli Δτ = γp Δt. Saadaan[1]
Yhtälö kerrotaan arvolla c2, jotta hieman edempänä saadaan oikeanlaisia yksiköitä[1]
Jos liikkuva kappale onkin levossa suhteessa sitä mittaavaan inertiaalikoordinaatistoon, on kappale samassa koordinaatistossa. Tällöin myös p = 0 ja γp = 1, joten (pc)2 sulkeutuu nollalla kerrottaessa pois, mutta yhdellä kerrottu (mc2)2 jää invariantiksi eli kaikissa koordinaatistoissa yhteneväksi arvoksi. Saadaan siis[1]
Otettaessa neliöjuuri yhtälön molemmilta puolilta, havaitaan että mc2 on myös invariantti arvo. Kahden inertiaalikoordinaatiston S ja S' vertailijat mittaavat häiriöttä vakionopeudella liikkuvalle kappaleelle eri liikemäärän, mutta molempien mittausten mukaan kappaleen liikemäärä konservoituu eli pysyy koordinaatistoissa muuttumattomana. Kahden ylemmän yhtälön mukaan γpmc2 on myös säilyvä ominaisuus. Yksikköinä γp on yksikötön, m on kg ja c2 on m2/s2. kg · m2/s2 on joule, joka on energian yksikkö. Oletetaan että kappaleen nopeus on paljon pienempi kuin tyhjiön valonnopeus, eli v ≪ c. Tällöin binomiaali approksimaatiota käyttäen saadaan kaava[1]
½mv2 on klassisen fysiikan liike-energian kaava, eli yhtälö antaa tyhjiön valonnopeutta paljon pienemmillä nopeuksilla samoja tuloksia kuin klassinen fysiikka. mc2 yhtälössä kertoo että massa sisältäisi energiaa.[1]
Massallisen kappaleen ollessa levossa eli kun v=0, saadaan yhtälöstä kappaleen lepoenergia E0 eli[1]
Liike-energia kappaleelle olisi siten[1]
Massan ja energian yhtäläisyys[muokkaa | muokkaa wikitekstiä]
Kahdella samamassaisella ja samalla nopeudella törmäävällä kappaleella on liike-energia K. Koska kappaleita on kaksi, on niiden liike-energia yhteensä 2K. Kappaleet törmäävät toisiinsa kohtisuoraan ja tarttuvat tai sulautuvat toisiinsa pysyvästi eli tapahtuu epäkimmoinen törmäys. Klassisessa fysiikassa 2K energian sanotaan muuttuvan kappaleiden atomien lämpöliikkeeksi, joka kohottaa kappaleiden lämpötilaa. Suhteellisuusteorian yhtälöön E = E0 + K ei kuitenkaan sisälly lämpöenergiaa. Törmäyksen energia on Et = 2mc2 + 2K. Kappaleet eivät liiku törmäyksen jälkeen, joten 2K = 0, ja kaava on siten[1]
Kaavassa M on yhteen sulautuneiden kappaleiden kokonaismassa. Energian on monesti osoitettu kokeellisesti olevan pysyvää, eli kappaleiden kokonaisenergia Ekok ei voi kadota törmäyksen jälkeenkään. Valonnopeus tyhjiössä on vakio, joten ainoa mahdollinen muuttuja on M.[1]
Massa ei siis säily eli se voi muuntua energiaksi. Vastavuoroisesti massaa voi muodostua energiasta. Tämän vastoin klassisen fysiikan perusperiaatteisiin kuuluvaa massan säilymislakia.[1] On kuitenkin hyvä ymmärtää, että energiaa itsessään ei ole missään puhtaassa muodossa, vaan se on täysin kuvitteellinen käsite, jolla voidaan vertailla eri asioita kuten liikettä ja kemiallisia reaktioita keskenään. Energia on siis verrannollisuuskerroin.
Suhteellisuusteorian massan ja energian yhtäläisyys on kuitenkin todistettu kokeellisesti monesti ja nimenomaan siihen perustuvat muun muassa ydinvoima ja ydinaseet, joissa pieni määrä massaa muuntuu valtavaksi määräksi energiaa.[1] Kyseessä ei kuitenkaan ole ydinreaktioihin rajoittunut tapahtuma: massan muuntumista energiaksi ja päinvastoin tapahtuu esimerkiksi kaikissa kemiallisissa reaktioissa kaikkialla koko ajan, mutta näiden energiat ovat pieniä suhteessa ydinreaktioihin ja massan muutokset ovat niin pieniä että ne ovat käytännössä merkityksettömiä. Kemiallisessa reaktiossa vapautunut energia myös usein muuntuu nopeasti ympäristön massaksi.[9][10]
Esimerkiksi kun hiukkaskiihdyttimessä kiihdytetään elektroni hyvin lähelle tyhjiön valonnopeutta ja törmäytetään se atomiin, voi elektroni irrottaa atomista elektronin. Klassisen fysiikan olettamusten pohjalta havaittaisiin kahden elektronin sinkoavan poispäin atomista, yhden irronneen ja yhden törmänneen. Oikeasti kuitenkin havaitaan sinkoavan atomista poispäin kolmen elektronin ja positronin, joka elektronin positiivisen omaava antimateriahiukkanen. Systeemin kokonaissähkövaraus pysyy muuttumattomana koska positroni ja elektroni sulkevat pois toistensa varaukset, mutta massan omaavat elektroni ja positroni ovat siis muodostuneet energiasta. Jokin elektroneista tosin annihiloituu erittäin nopeasti positronin kanssa, koska materia ja antimateria reagoivat keskenään kiivaasti, jolloin nämä kaksi hiukkasta katoavat ja muuntuvat kahdeksi vastakkaisiin suuntiin eteneväksi ja massattomaksi fotoniksi. Fotonit varastoivat elektronin ja positronin liike-energian ja massan energian taajuuteensa.[1]
Kausaliteetin rikkoutuminen[muokkaa | muokkaa wikitekstiä]
Massallinen tai massaton hiukkanen ei voi liikkua valoa nopeammin sillä se rikkoisi suppeassa suhteellisuusteoriassa kausaliteetin. Kausaliteetilla fysiikassa tarkoitetaan syy-seuraussuhdetta eli jokin tapahtuma A aiheuttaa tapahtuman B. Suppean suhteellisuusteorian Lorentz-muunnoksilla laskettaessa valoa nopeammin liikkuvan kappaleen on pakko saada aikaan B ennen A:ta jossakin toisessa inertiaalikoordinaatistossa. Kiven heittäminen eli tapahtuma A välittyy kiven liikkeen, joka on kausaliteetin välittäjä, kautta tapahtumaksi B, jossa kivi rikkoo liikkuvan auton ikkunan. Tilannetta, jossa ikkuna rikkoutuu ennen kiven osumista siihen, ei ole koskaan havaittu käytännössä. Massallinen kappale, kuten kivi, vaatii suppean suhteellisuusteorian mukaan lisäksi äärettömästi energiaa liikkuakseen valoa nopeammin. Tilanne on kuitenkin edelleen mahdoton vaikka kiven sijaan käytettäisiin jotakin massatonta sädettä, joka liikkuu valoa nopeammin räjäyttäen vaikkapa pommin ikkunassa osuttuaan pommissa olevaan säteen havaitsimeen. Vastaavanlaiset tapahtumat aiheuttavat paradokseja. Tilanne, jossa henkilö syntyy ennen äitiään, olisi kausaliteetin rikkoutuessa "mahdollinen". On hyvä ottaa huomioon, että vaikka toisistaan riippumattomat tapahtumat ovat aina eri aikaisia eri inertiaalikoordinaatistoissa suppean suhteellisuusteorian mukaan (katso osio samanaikaisuuden suhteellisuus), ovat tapahtumat edelleen toisistaan riippumattomia, eli niiden välillä ei ole kausaalista suhdetta.[1]
Oletetaan että A aiheuttaa tapahtuman B jonkin aiheuttajan välittämänä, jonka nopeus on u. Aiheuttaja liikkuu valon tyhjiönopeutta c nopeammin eli u > c. Tapahtuma A tapahtuu inertiaalikoordinaatistossa S kohdassa xA = 0 ajan hetkenä tA = 0. A aiheuttaa tapahtuman B toisessa inertiaalikoordinaatistossa S', joka liikkuu valoa hitaammin nopeudella v eli v < c. B tapahtuu koordinaatiston S' kohdassa xB ajan hetkenä tB = xB / u.[1]
Koska xA = 0 ja tA = 0, on Lorentz-muunnosten mukaan xA' = 0 ja tA' = 0. Lorentz-muunnos tapahtuman B ajan hetkelle tB' on[1]
Yhtälöstä on poistettu tB, koska u = xB / tB inertiaalikoordinaatistossa S. u on jonkin kertoimen α verran valoa nopeampi eli u = αc. α > 1, jotta u > c. Siten yhtälön vu/c2 = αv/c. Lopullisen yhtälön lähemmässä tarkastelussa nähdään että[1]
- v > c/α, koska α > 1. Siten vu/c2 > 1.
- Koska vu / c2 > 1, on yhtälön (1 - vu / c2) arvo negatiivinen eli tB' < 0.
- Jos tB' < 0, silloin B tapahtuu ennen A:ta inertiaalikoordinaatistossa S'. Kausaliteetti on rikkoutunut inertiaalikoordinaatistossa S'.
Katso myös[muokkaa | muokkaa wikitekstiä]
Lähteet[muokkaa | muokkaa wikitekstiä]
- ↑ a b c d e f g h i j k l m n o p q r s t u v w x y z aa ab ac ad ae af ag ah ai aj ak al am an ao ap aq ar as at au av aw ax ay az ba bb bc bd be bf bg bh bi bj bk bl bm bn bo bp bq br bs RD Knight et al: Physics for scientists and engineers: a strategic approach, s. 1060–1097. 3. painos. Pearson Education inc, 2013. ISBN 9780321740908.
- ↑ A Einstein: Zur elektrodynamik bewegter Körper. (Käännös englanniksi) Annalen der Physik, 1905, 322. vsk, nro 10, s. 891–921. doi:10.1002/andp.19053221004. ISSN 0003-3804. Artikkelin verkkoversio.
- ↑ A Einstein: Ist die trägheit eines körpers von seinem energieinhalt abhängig? (Käännös englanniksi) Annalen der Physik, 1905, nro 18, s. 639–641. doi:10.1002/andp.19053231314. ISSN 0003-3804. Artikkelin verkkoversio.
- ↑ a b S Banerji, A Banerjee: Special theory of relativity, s. 20. PHI Learning Pvt. Ltd., 2004. ISBN 9788120319639.
- ↑ JC Maxwell: VIII. A dynamical theory of the electromagnetic field. Philosophical Transactions of the Royal Society of London, 1865, 155. vsk, s. 459–512. doi:10.1098/rstl.1865.0008. ISSN 0261-0523. Bibcode:1865RSPT..155..459C. Artikkelin verkkoversio.
- ↑ a b RA Serway et al: Physics for scientists and engineers, s. 1145–1176. 8. painos. Brooks/Cole, Cengage Learning, 2010. ISBN 9780495827818.
- ↑ RJ Kennedy, EM Thorndike: Experimental establishment of the relativity of time. Physical Review, 1932, 42. vsk, nro 3, s. 400–418. doi:10.1103/PhysRev.42.400. ISSN 1536-6065. Artikkelin verkkoversio.
- ↑ What would a relativistic interstellar traveller see? math.ucr.edu. Arkistoitu 17.5.2018. Viitattu 27.5.2018.
- ↑ Why is mass conserved in chemical reactions? Science Questions with Surprising Answers. Arkistoitu 19.7.2017. Viitattu 31.5.2018.
- ↑ RS Treptow: E = mc2 for the chemist: when is mass conserved? Journal of Chemical Education, 2005, 82. vsk, nro 11, s. 1636. doi:10.1021/ed082p1636. ISSN 0021-9584. Artikkelin verkkoversio.
Aiheesta muualla[muokkaa | muokkaa wikitekstiä]
- Einstein, Albert: Zur Elektrodynamik bewegter Körper. Annalen der Physik, 1905, 322. vsk, nro 10, s. 891–921. Artikkelin verkkoversio. (saksaksi)
- Turun yliopisto, Erikoinen suhteellisuusteoria
- Thuneberg, Erkki: Johdatus suhteellisuusteoriaan (pdf) (Suppean suhteellisuusteorian luentomoniste) users.aalto.fi. Oulun yliopisto.
- Scholarpedia: Special relativity (englanniksi)
- Scholarpedia: Special relativity: electromagnetism (englanniksi)
- Scholarpedia: Special relativity: kinematics (englanniksi)
- Scholarpedia: Special relativity: mechanics (englanniksi)












































