Tikapuuparadoksi
Tikapuuparadoksi (eli seiväs ladossa -paradoksi[1] tai lipputankoparadoksi[2]) on suppeaan suhteellisuusteoriaan liittyvä ajatuskoe. Siinä oletetaan, että vaakasuoraan asentoon, maan pinnan suuntaisesti asetettuja tikapuita kuljetetaan vaakasuorasti suhteellisuusteoreettisella nopeudella, toisin sanoen nopeudella, joka on siinä määrin lähellä valonnopeutta, että pituuskontraktio eli Lorentz-kontraktio on havaittavissa. Tikapuiden tai muun pitkänomaisen esineen (esimerkiksi seipään tai lipputangon) oletetaan kulkevan etu- ja takaoven kautta sellaisen autotallin tai ladon läpi, jonka pituus on pienempi kuin tikapuiden lepopituus, niin että jos tikapuut eivät olisi liikkeessä, ne eivät mahtuisi sisään. Maan suhteen levossa olevan havaitsijan kannalta näyttää kuitenkin pituuskontraktion vuoksi siltä, että kulkiessaan autotallin läpi tikapuut mahtuvat sinne kokonaisuudessaan ja ovat hetken aikaa kokonaan sisällä. Sen sijaan tikkaiden mukana liikkuvan havaitsijan näkökulmasta tikkaat eivät kutistu kokoon, kun taas autotalli tulee pituuskontraktion vuoksi entistäkin lyhemmäksi, joten tikapuut eivät mahdu kokonaisuudessaan sisään. Tästä näyttää seuraavan, että eri havaitsijoiden kannalta sinänsä yhtä todelliset tilanteet ovat ristiriidassa keskenään.
Tämä näennäinen paradoksi seuraa siitä, että virheellisesti oletetaan absoluuttinen samanaikaisuus. Tikapuiden sanotaan mahtuvan autotalliin, jos niiden molemmat päät voivat samanaikaisesti olla autotallin sisällä. Paradoksi ratkeaa, kun otetaan huomioon, että suhteellisuusteorian mukaan tapahtumien samanaikaisuus on suhteellinen, minkä vuoksi myös vastaus kysymykseen siitä, ovatko tikkaiden molemmat päät samanaikaisesti autotallista, riippuu havaitsijan liiketilasta ja sen mukaisesti käytetystä koordinaatistosta.
Paradoksi[muokkaa | muokkaa wikitekstiä]
Yksinkertaisimmassa muodossaan paradoksissa oletetaan autotalli, jonka etu- ja takaovet ovat molemmat avoimia, ja tikapuut, jotka ollessaan levossa autotallin suhteen ovat liian pitkät mahtuakseen sisään. Oletetaan, että tikapuita kuljetetaan suurella vaakasuoralla nopeudella levossa olevan autotallin läpi. Tikkaiden suuren nopeuden vuoksi niihin vaikuttaa suhteellisuusteoreettinen pituuskontraktio, ja ne tulevat merkittävästi lyhyemmiksi. Sen vuoksi tikapuut ovat autotallin läpi kulkiessaan hetkellisesti kokonaisuudessaan sisällä. Olisi periaatteessa mahdollista sulkea samanaikaisesti molemmat ovet sen toteamiseksi, että tikkaat ovat sisällä.
Tähän saakka kaikki on selvää. Paradoksi seuraa tilanteen symmetrisyydestä. Oletetaan, että tikkaiden mukana liikkuu toinen havaitsija, jonka nopeus autotallin lepokoordinaatistossa on sama kuin tikkaiden. Suhteellisuusperiaatten mukaisesti samat fysiikan lait kuitenkin pätevät myös tämän havaitsijan lepokoordinaatiosta. Hänen näkökulmastaan tikkaat ovat levossa ja autotalli liikkuu suurella nopeudella. Siitä kuitenkin seuraa, että tikkaiden sijasta lyheneekin autotalli, joka on aivan liian pieni, jotta tikkaat mahtuisivat sisään, eikä molempia ovia voida sulkea samanaikaisesti tikkaiden ollessa sisällä. Tämä näennäinen ristiriita tunnetaan tikapuuparadoksina.
Ratkaisu[muokkaa | muokkaa wikitekstiä]
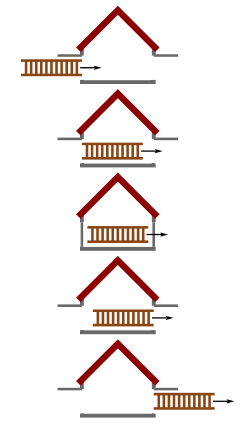
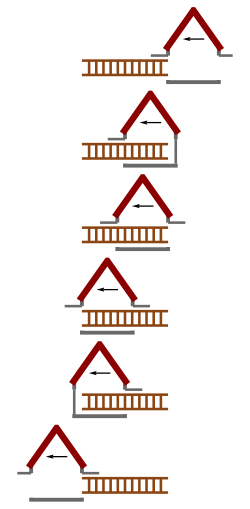
Paradoksin ratkaisee samanaikaisuuden suhteellisuus: kaksi tapahtumaa, jotka yhden, esimerkiksi autotallissa olevan havaitsijan kannalta ovat samanaikaisia, eivät välttämättä ole samanaikaisia toisen, esimerkiksi tikapuiden mukana liikkuvan havaitsijan kannalta. Kun sanotaan, että tikapuut "mahtuvat" sisään autotalliin, tarkoitetaan täsmällisemmin sanottuna sitä, että jonakin tiettynä hetkenä tikapuiden alku- ja loppupää ovat molemmat samanaikaisesti sisällä autotallissa, toisin sanoen tikapuut ovat jollakin hetkellä kokonaisuudessaan sisällä autotallissa.[1] Koska samanaikaisuus on suhteellista, toisen havaitsijan vertailujärjestelmässä sellaista hetkeä ei välttämättä ole. Autotallin vertailujärjestelmässä eli sen lepokoordinaatistossa tikkaiden molemmat päät olivat samanaikaisesti sisällä autotallissa, sillä ne mahtuivat sisään, mutta tikapuiden vertailujärjestelmässä nämä tapahtumat eivät olleet samanaikaisia eivätkä tikkaat millään hetkellä olleet kokonaisuudessaan sisällä.
Asiaa voidaan selventää olettamalla, että autotallin vertailujärjestelmässä sen molemmat ovet suljetaan hetkeksi samanaikaisesti tikkaiden ollessa sisällä. Tarkastellaan samoja tapahtumia tikapuiden vertailujärjestelmässä. Ensin tikapuiden alkupää lähestyy autotallin poistumisovea. Ovi sulkeutuu ja avautuu jälleen, niin että tikapuut pääsevät ulos. Vasta myöhemmin tikapuiden loppupää kulkee autotallin etuovesta sisään, minkä jälkeen tämä ovi suljetaan ja jälleen avataan. Todetaan, että samanaikaisuus on suhteellista. Tikapuiden vertailujärjestelmässä molemmat ovet eivät sulkeutuneet samanaikaisesti eikä tikkaiden tarvitse mahtua sisään autotalliin.
Tilannetta voidaan vielä havainnollistaa alla olevalla Minkowskin diagrammilla. Diagrammi esittää autotallin vertailujärjestelmää. Pystysuora vaaleansininen suorakulmio osoittaa autotallin aika-avaruudessa ja vaaleanpunainen suunnikas tikkaita aika-avaruudessa. Kaavion x- ja t-akselit ovat paikka- ja aika-akselit autotallin, x′ ja t′ taas tikkaiden vertailujärjestelmässä.
Autotallin vertailujärjestelmässä tikapuita millä tahansa hetkellä esittää vaaleanpunaisen suunnikkaan läpi kulkeva vaakasuora, x-akselin suuntainen jana. Yksi sellainen on kaavioon sinisellä merkitty jana AB, joka on kokonaan vaaleansinisen, autotallia kuvaavan suorakulmion sisällä ja esittää tikapuita hetkellä, jolloin ne ovat kokonaan sisällä autotallissa. Tikkaiden vertailujärjestelmässä sitä vastoin samanaikaisia ovat ne tapahtumat, joiden vastinpisteet ovat samalla x'-akselin suuntaisella janalla. Tikapuita millä tahansa hetkellä esittää näin ollen x'-akselin suuntainen, punaisen suunnikkaan läpi kulkeva jana, kaaviossa esimerkiksi jana AC. Nähdään, etteivät mikään tällainen jana mahdu kokonaisuudessaan vaaleansinisen suorakulmion sisään, toisin sanoen tikapuut eivät millään hetkellä ole kokonaisuudessaan autotallin sisällä.

Tikkaiden sulkeminen autotalliin[muokkaa | muokkaa wikitekstiä]

Hieman monimutkaisempi versio paradoksista saadaan, jos tikapuut suljetaan sisään autotalliin niiden ollessa kokonaan sisällä. Tämä voidaan saada aikaan esimerkiksi niin, että poistumisovea ei sen sulkemisen jälkeen avata uudelleen. Autotallin vertailujärjestelmässä voidaan olettaa, ettei poistumisovi ole liikkeessä, ja niinpä kun tikapuut osuvat siihen, sanotaan, että ne yhtäkkisesti pysähtyvät.[3] Wolfgang Rindler kuvaili tilannetta sauvalla, joka kiihtyy samanaikaisesti. Sillä hetkellä myös se ovi, josta tikkaat tulivat sisään, on kiinni, joten tikkaat jäävät sisään autotalliin. Koska niiden suhteellinen nopeus on nyt nolla, ne eivät enää ole pituuskontraktoituneet ja ovat nyt pidemmät kuin autotalli; niinpä niiden tulisi taipua, katketa tai räjähtää.
Tässäkin tapauksessa ongelmia aiheuttaa tilanteen tarkasteleminen tikapuiden vertailujärjestelmässä. Omassa vertailujärjestelmässään tikapuut ovat aina pidempiä kuin autotalli. Kuinka ovet siis voidaan sulkea niin, että tikapuut jäävät sisään?
Tässä on huomattava yksi suhteellisuusteorialle ominainen yleinen piirre. Tarkastelemalla tilannetta autotallin kannalta olemme päätelleet että tikapuut on mahdollista sulkea sisään. Tämän täytyy kuitenkin olla totta kaikissa vertailujärjestelmissä – ei voi olla niin, että ne jäävät sisään yhdessä vertailujärjestelmässä, mutta eivät toisessa. Näin ollen myös tikkaiden vertailujärjestelmässä on oltava selitys sille, että ne voidaan sulkea sisään autotalliin; tämä selitys on vain löydettävä.
Ratkaisu on, että vaikka tikkaiden kaikkien osien nopeus autotallin vertailujärjestelmässä pienenee nollaan samanaikaisesti, mutta samanaikaisuuden suhteellisuuden vuoksi tikkaiden eri osien hidastumiset eivät niiden omassa vertailujärjestelmässä ole samanaikaisia. Itse asiassa tikkaiden eri osien liike hidastuu eri aikaan, toinen toisensa jälkeen hidastuvat toinen toistensa jälkeen[3], ensin niiden etupään ja viimeiseksi niiden takapään liike hetkellä, jolloin se on jo autotallissa.
Tikapuuparadoksi liittyy pituuskontraktioon vastaavalla tavalla kuin kaksosparadoksi aikadilataatioon, joka pituuskontraktion tavoin sekin on Lorentzin muunnoksen ilmenemismuoto. Kaksosparadoksissa oletetaan, että toinen kaksosveljistä lähtee Maasta, liikkuu avaruudessa suurella nopeudella ja palaa Maahan veljeään nuorempana. Samaan tapaan kuin tikapuuparadoksissa tikapuut ja autotalli liikkuvat toistensa suhteen, on kaksosparadoksissakin kysymys siitä, että molemmat veljekset liikkuvat toistensa suhteen, jolloin suhteellisuusperiaatteen mukaisesti molempien voisi olettaa olevan samanarvoisessa asemassa. Kummassakaan tapauksessa eri vertailujärjestelmät eivät kuitenkaan ole yhtäläisessä asemassa, sillä vain toinen osapuoli (tikapuuparadoksissa tikapuut, kaksosparadoksissa avaruusmatkaaja) joutuu kiihtyvään liikkeeseen, joka rikkoo tilanteen symmetrian. (Ellei avaruusmatkaaja missään vaiheessa joutuisi kiihtyvään liikkeeseen, hän liikkuisi aina vain suoraan poispäin Maasta eikä koskaan palaisi.)

Tikapuuparadoksi ja voiman välittyminen[muokkaa | muokkaa wikitekstiä]

Tarkastellaan, mitä tapahtuu, jos autotallin takaovi, josta tikapuut tulevat ulos, on pysyvästi suljettu eikä sitä missään vaiheessa avata. Oletetaan, että ovi on niin luja, ettei se hajoa tikkaiden törmätessä siihen, joten tikkaiden on pysähdyttävä. Kuten edellä esitetyssä tapauksessa, autotallin vertailujärjestelmässä on nytkin hetki, jolloin tikapuut ovat kokonaan sisällä, toisin sanoen niiden loppupää on kulkenut etuoven ohi, ennen kuin se törmää takaseinään ja pysähtyy. Tikapuiden vertailujärjestelmässä tikkaat ovat kuitenkin liian pitkät mahtuakseen autotalliin, joten törmäyksen hetkellä tikkaiden loppupää ei ole vielä kulkenut etuoven ohi. Tämä näyttää paradoksilta. Kysymys on, kulkeeko tikkaiden loppupää etuoven ohi vai eikö.
Vaikeus seuraa pääasiassa oletuksesta, että tikkaat ovat jäykkä kappale, toisin sanoen se ei muuta muotoaan. Arkielämässä tikkaat vaikuttavatkin jäykiltä. Mutta kappale voisi olla täysin jäykkä vain, jos voima välittyisi sen läpi äärettömän nopeasti. Toisin sanoen jos kappaleen toista päätä työnnetään, sen toisen pään olisi reagoitava samalla hetkellä, muussa tapauksessa kappaleen muoto muuttuu. Tämä on vastoin suppeaa suhteellisuusteoriaa, jonka mukaan informaatio ei voi edetä valoa nopeammin. Tällä seikalla ei yleensä ole havaittavia seurauksia arkielämässä, mutta tikapuuparadoksin ratkaisun kannalta tämä on oleellinen asia. Suppean suhteellisuusteorian mukaan ei siis voi olla olemassa täysin jäykkiä kappaleita.[2]
Sillä hetkellä kun tikapuiden alkupää törmää takaseinään, niiden loppupää ei vielä "tiedä" niin tapahtuneen, ja näin ollen se jatkaa liikettään tasaisella nopeudella suoraan eteenpäin. Tämä ilmenee tikkaiden puristumisena kokoon. Sekä autotallin että tikkaiden vertailujärjestelmässä tikkaiden loppupää jatkaa liikettään törmäyksen aikana ainakin siihen hetkeen saakka, jolloin törmäystapahtuman valokartio saavuttaa tikkaiden loppupään, toisin sanoen hetkeen, jolloin törmäyksestä valonnopeudella lähtenyt signaali saavuttaisi tikkaiden loppupään. Sillä hetkellä tikkaat ovat itse asiassa alkuperäistä kontraktoitunutta pituuttaan lyhempiä, joten niiden loppupää mahtuu vielä autotalliin. Molemmissa vertailujärjestelmissä suoritetut laskut vahvistavat tämän.
Tämä teoreettinen tarkastelu ei kuitenkaan riitä selvittämään, mitä tikkaille tapahtuu sen jälkeen, kun voima on saavuttanut niiden loppupään (vihreän alueen oheisessa diagrammissa). Tikkaiden materiaalista riippuen ne todennäköisesti murskautuvat, mutta jos ne olisivat tarpeeksi kimmoiset ja sitkeät, periaatteessa ne voisivat taipua ja sen jälkeen jopa laajeta takaisin alkuperäiseen pituuteensa. Tarpeeksi suurilla nopeuksilla mikä tahansa todellinen materiaali kuitenkin räjähtäisi tällaisessa törmäyksessä suurella voimalla plasmaksi.
Kuoppaan putoava ihminen[muokkaa | muokkaa wikitekstiä]

Erään muunnetun version tikapuuparadoksista esitti ja ratkaisi Wolfgang Rindler.[3] Hän tarkasteli ajatuskokeessaan nopeasti kävelevää ihmistä, jonka hän paradoksia kuvaillessaan korvasi sauvalla ja joka äkillisesti putosi syvään kuoppaan.[4] Oletettiin, että kuopan vertailujärjestelmässä sauva oli kokonaan kuopassa ennen kuin sen kiihtyvä liike alaspäin alkoi samanaikaisesti sauvan jokaisessa kohdassa.
Kuopan vertailujärjestelmässä sauva kokee pituuskontraktion ja mahtuu kuoppaan. Sauvan vertailujärjestelmässä kontraktion kuitenkin kokee kuoppa, ei sauva, minkä vuoksi sauva vaikuttaa liian lyhyeltä mahtuakseen koko pituudeltaan kuoppaan.
Sauvan alaspäin suuntautuva kiihtyvyys on sen joka kohdassa samanaikainen kuopan vertailujärjestelmässä. Sauvan vertailujärjestelmässä näin ei kuitenkaan ole laita, vaan pystysuoran kiihtyvyyden saan ensin sen etupää, jota esittää oheisen kaavion alin kerros. Ajan kuluessa yhä suurempi osa sauvasta saa alaspäin suuntautuvan kiihtyvyyden, kunnes lopulta koko sauva on kiihtyvässä liikkeessä. Tämä kuitenkin seuraa, että sauvan vertailujärjestelmässä sauva myös taipuu. Koska näin tapahtuu sauvan vertailujärjestelmässä, kyseessä on todellinen fysikaalinen muutos, joka aiheuttaa jännityksiä sauvan sisällä.
Putoavaa sauvaakaan ei siis voida pitää täysin jäykkänä kappaleena. Jotta tämä taipuminen olisi havaittavissa, sekä sauvan pituuden että kuopan syvyyden on kuitenkin oltava niin suuret, että putoamiseen kuluva aika on mitattavissa.
Tanko- ja rengasparadoksi[muokkaa | muokkaa wikitekstiä]

Sauva- ja kuoppaparadoksia muistuttaa myös Rafael Ferraron vuonna 2007 esittämä tangon ja renkaan ongelma, joka kuitenkin on oleellisesti yksinkertaisempi.[5] Edellä esitettyä sauva- ja kuoppaparadoksia mutkistaa se seikka, että tilanteen kuvaamiseen on käytettävä myös ei-inertiaalisia koordinaatistoja, koska tilanteeseen liittyy eri suuntaisia liikkeitä: ensin ihminen kävelee vaakasuoraan ja sitten putoaa pystysuoraan, jota paitsi toisessa vertailujärjestelmässä ihminen tai vastaava sauva myös kaareutuu, kun taas toisessa se pysyy suorana. Tämä herättää helposti kysymyksen sauvan sitkeydestä, joka on omiaan hämärtämään "paradoksin" todellisen luonteen. Tanko- ja rengasparadoksiin ei tällaisia mutkistavia lisäpiirteitä liity. Siinä oletetaan, että tanko, jonka pituus on hieman suurempip kuin renkaan läpimitta, on liikkeessä yläoikealle, kun taas rengas on levossa vaakasuorassa tasossa. Jos tangon liike on sellainen, että jollakin hetkellä sen keskipiste on renkaan keskipisteessä, tanko on Lorentz-kontraktoitunut liikkeensä eteenpäin suuntautuvan komponenttinsa vuoksi ja se mahtuu kulkemaan renkaan läpi. Paradoksi ilmenee, kun tilannetta tarkastellaan tangon lepokoordinaatistossa. Siinä rengas on liikkeessä alavasemmalle ja on Lorentz-kontraktoitunut vaakasuorassa suunnassa, kun taas tanko ei ole lainkaan kontraktoitunut. Kuinka tanko siis pääsee renkaan läpi?
Tässäkin tapauksessa paradoksin ratkaisu liittyy samanaikaisuuden suhteellisuuteen.[5] Fysikaalisen kappaleen pituus määritellään kahden samanaikaisen tapahtuman etäisyytenä, jotka tapahtuvat sen kummassakin päässä, ja koska samanaikaisuus on suhteellista, on samoin tämän pituuden laita.[2] Tämä pituuden vaihtelevuus on juuri Lorentz-kontraktio. Samoin fysikaalinen kulma määritellään kolmen samanaikaisen tapahtuman välisenä kulmana, ja sekin on samalla tavalla suhteellinen suure. Tässä esitetyssä paradoksissa sauva on renkaan tason suuntainen renkaan, mutta ei sauvan lepokoordinaatistossa. Kontraktoitumaton sauva pääsee kulkemaan Lorentz-kontraktoituneen renkaan sisäpuolitse, koska sauvan lepokoordinaatistossa rengas on siinä määrin vinossa asennossa sauvaan nähden, että sauva mahtuu kulkemaan sen sisäpuolitse.
Matemaatisin termein Lorentz-muunnos voidaan esittää avaruudellisen kiertymisen ja "puhtaan" Lorentz-muunnoksen tulona, joista jälkimmäinen ei sisällä avaruudellista kiertymistä. Sauva- ja rengasparadoksin matemaattinen ratkaisu perustuu siihen, että kahden puhtaan Lorentz-muunnoksen (vaakasuoran ja pystysuoran) tulo ei välttämättä ole puhdas (tässä tapauksessa viistoa liikettä vastaava) Lorentz-kontraktio, vaan se voi sisältää avaruudellisen kiertymiskomponentin.
Lähteet[muokkaa | muokkaa wikitekstiä]
- Willard H. Wells: Length paradox in relativity. American Journal of Physics, 1961, 29. vsk, nro 12. doi:10.1119/1.1937641.
- R. Shaw: Length contraction paradox. American Journal of Physics, 1962, 30. vsk, nro 1. doi:10.1119/1.1941907.
- Roberto De A. Martins: Length paradox in relativity. American Journal of Physics, 1978, 46. vsk, nro 6, s. 667–670. doi:10.1119/1.11227.
- G. P. Sastry: Is length contraction really paradoxical?. American Journal of Physics, 1987, 55. vsk, nro 10, s. 943–946. doi:10.1119/1.14911.
- Øyvind Grøn, Steinar Johannesen: Computer simulation of Rindler's length contraction paradox. European Journal of Physics, 1993, 14. vsk, nro 3, s. 97–100. doi:10.1088/0143-0807/14/3/001.
- Harald van Lintel, Christian Gruber: The rod and hole paradox re-examined. European Journal of Physics, 2005, 26. vsk, nro 1, s. 19–23. doi:10.1088/0143-0807/26/1/003. Artikkelin verkkoversio.
- Chandry Iyer, G. M. Prabhu: Reversal in the time order of interactive events: the collision of inclined rods. European Journal of Physics, 2008, 27. vsk, nro 4, s. 819–824. doi:10.1088/0143-0807/27/4/013.
- Evan Pierce: The lock and key paradox and the limits of rigidity in special relativity. American Journal of Physics, 2007, 75. vsk, nro 7, s. 610–614. doi:10.1119/1.2711827.
- CHandru Iyer, G. M. Prabhu: Differing observations on the landing of the rod into the slot. American Journal of Physics, 2008, 74. vsk, nro 11, s. 998–1001. doi:10.1119/1.2346686.
- Enda McGlynn, Enda, Paul van Kampen: A note on linking electric current, magnetic fields, charges and the pole in a barn paradox in special relativity. European Journal of Physics, 2008, 29. vsk, nro 6, s. N63–N67. doi:10.1088/0143-0807/29/6/N03.
Viitteet[muokkaa | muokkaa wikitekstiä]
- ↑ a b Richard A. Muller: ”Ristiriitoja ja paradokseja: Seiväs ladossa -paradoksi”, Nyt: Ajan fysiikka, s. 47. Suomentanut Kimmo Pietiläinen. Terra Cognita, 2016. ISBN 978-952-5697-81-0.
- ↑ a b c Lorentzin muunnosten fysikaalisia seurauksia Helsingin yliopiston fysiikan laitos. Viitattu 27.5.2020. [vanhentunut linkki]
- ↑ a b c Wolfgang Rindler: Length Contraction Paradox. American Journal of Physics, 1961, 29. vsk, nro 6, s. 365–366. doi:10.1119/1.1937789.
- ↑ Edwin F. Taylor, John Archibald Wheeler: Spacetime Physics: Introduction to Special Relativity, s. 116. New York: W. H. Freeman, 1992. ISBN 0-7167-2327-1. Teoksen verkkoversio.
- ↑ a b Rafael Ferraro: Einstein's space-time: an introduction to special and general relativity. Springer, 2007. ISBN 978-0-387-66946-2.
Aiheesta muualla[muokkaa | muokkaa wikitekstiä]
 Kuvia tai muita tiedostoja aiheesta Tikapuuparadoksi Wikimedia Commonsissa
Kuvia tai muita tiedostoja aiheesta Tikapuuparadoksi Wikimedia Commonsissa



