Derivaatta

Funktion kuvaaja (mustalla) ja erästä sen pistettä sivuava tangettisuora (punaisella). Tuon tangenttisuoran kulmakerroin on funktion derivaatta kyseisessä pisteessä.

Matematiikassa derivaatta kuvaa funktion paikallista muutosnopeutta. Geometrisesti derivaattaa voidaan havainnollistaa funktion kuvaajan tangentin (sivuajan) kulmakertoimena. Täsmällisesti derivaatta määritellään raja-arvon avulla. Käsitteellä funktion derivaatta voidaan tarkoittaa joko yhtä lukuarvoa, funktion muutosnopeutta tietyssä pisteessä, tai vaihtoehtoisesti toista funktiota, jonka arvo jokaisessa pisteessä on alkuperäisen funktion derivaatta. Jälkimmäisessä tapauksessa voidaan puhua myös derivaattafunktiosta. Derivaatan arvon määrittämistä tai funktion derivaattafunktion määrittämistä kutsutaan derivoinniksi.

Derivaatan käsitteen esittivät ensimmäisenä Isaac Newton ja Gottfried Leibniz 1600-luvulla. Sanan derivaatta (johdos) otti käyttöön Joseph-Louis Lagrange 1700-luvun lopulla.

Derivaatalla on monia hyödyllisiä sovelluksia fysiikassa, insinööritieteissä, taloustieteissä ja kaikkialla, missä joudutaan tarkastelemaan toisista suureista riippuvien suureiden muuttumisominaisuuksia.

Derivoinnin (jolla nyt tarkoitetaan jonkin funktion derivaattafunktion määrittämistä) käänteisoperaatio on integrointi, silloin kun integroinnilla tarkotetaan funktion integraalifunktion määrittämistä.

Derivaatan täsmällinen määritelmä

Olkoon $f\,$ reaali- tai kompleksimuuttujan reaali- tai kompleksiarvoinen funktio. Jos $f\,$ on määritelty pisteen $x_0\,$ ympäristössä (eli avoimessa joukossa, joka sisältää $x_0\,$:n), niin sen derivaatta pisteessä $x_0\,$ on funktion erotusosamäärän

${f(x_0+h)-f(x_0)\over h}$

raja-arvo

$f'(x_0):=\lim_{h\to 0}{f(x_0+h)-f(x_0)\over h}=\lim_{c\to x_0}{f(c)-f(x_0)\over c-x_0}.$

Derivaatta pisteessä $x_0\,$ on luonnollisesti olemassa vain, mikäli kyseinen raja-arvo on olemassa eli

$\forall {\epsilon>0} \, \exists {\delta>0} : |x-x_0|<\delta \Rightarrow \left|{f(x)-f(x_0)\over x-x_0}-f'(x_0)\right|<\epsilon$.

Toisin sanoen kaikille $\epsilon >0\,$ löytyy $\delta >0\,$ siten, että erotusosamäärän arvot ovat alle $\epsilon\,$:in päässä raja-arvosta eli derivaatan arvosta, kun muuttujan arvot ovat alle $\delta\,$:n päässä tarkasteltavasta pisteestä.

Mikäli funktiolla $f\,$ on derivaatta, eli erotusosamäärän raja-arvo pisteessä $x_0$, sanotaan että $f\,$ on derivoituva pisteessä $x_0\,$. Jos derivaatta on olemassa kaikissa $f\,$:n määrittelyjoukon pisteissä, niin sanotaan, että $f\,$ on derivoituva määrittelyjoukossaan. Tällöin myös funktiota

$x \mapsto \lim_{h\to 0}{f(x+h)-f(x)\over h}$

kutsutaan $f$:n derivaattafunktioksi.

Merkintätapoja

Derivaattafunktiolle on käytössä useita eri merkintöjä, esimerkiksi $f'\,$, $Df\,$, $\frac{df}{dx}\,$ ja $\dot f\,$. Viimeistä käytetään erityisesti silloin, kun $f\,$ on aikamuuttujasta riippuva funktio.

Funktion derivaattaa pisteessä $a\,$ merkitään vastaavasti $f'(a)\,$, $Df(a)\,$, $\left(\frac{df}{dx}\right)_{x=a}$ tai $\dot f(a)\,$.

Jos myös $f\,$:n derivaattafunktio on derivoituva, niin funktiota $f\,$ kutsutaan kahdesti derivoituvaksi, ja vastaavasti toiselle derivaatalle käytetään merkintöjä $f''\,$, $D^2 f(x)\,$ ja $\frac{d^2 f}{dx^2}$. Yleisemmin, jos $f\,$:n $(n-1)\,$:s derivaattafunktio on derivoituva, niin funktio on $n\,$ kertaa derivoituva, ja sen $n\,$:ttä derivaattaa merkitään $f^{(n)}\,$, $D^n f(x)\,$ ja $\frac{d^n f}{dx^n}\,$.

Jos funktion ($n\,$:s) derivaatta on olemassa ja jatkuva, niin funktion sanotaan olevan ($n\,$ kertaa) jatkuvasti derivoituva. Mikäli funktion $n\,$:s derivaattafunktio on olemassa ja jatkuva, sanotaan, että funktio on $C^n\,$-funktio. Jos funktio on äärettömän monta kertaa derivoituva ja sen jokainen derivaattafunktio on jatkuva, niin funktion sanotaan olevan $C^{\infty}\,$-funktio.

Yleisiä derivointisääntöjä

Säännön nimi	Derivointisääntö
Vakion derivaatta	$D c = 0\,$, kun $c\,$ on vakio.
Vakion siirto	$D c f(x) = c D f(x)\,$
Summan derivaatta	$D (f(x) + g(x)) = D f(x) + D g(x)\,$
Tulon derivaatta	$D (f(x) g(x)) = g(x)D f(x) + f(x)D g(x)\,$
Osamäärän derivaatta	$D \frac{f(x)}{g(x)} = \frac{g(x)D f(x) - f(x)D g(x)}{g(x)^2}$,
Yhdistetyn funktion derivaatta	$D g(f(x)) = g'(f(x)) f'(x)\,$
Käänteisfunktion derivaatta	$(f^{-1})'(f(x))= {1 \over f'(x)}\,$, jossa $f^{-1}\,$ on $f\,$:n käänteisfunktio

Tavallisten funktioiden derivaattoja

• Potenssin derivaatta

$D x^n = n x^{n-1}\,$, missä $n \in \mathbb{Z}$.

• Trigonometristen funktioiden ja niiden käänteisfunktioiden (arkusfunktioiden) derivaattoja

$D \sin x = \cos x\,$

$D \cos x = -\sin x\,$

$D \tan x = {1 \over \cos^2 x} = 1 + \tan^2 x$

$D \cot x = -{1 \over \sin^2 x} = -1 - \cot^2 x$

$D \arcsin x = {1 \over \sqrt{1-x^2}}$

$D \arccos x = -{1 \over \sqrt{1-x^2}}$

$D \arctan x = {1 \over 1+x^2}$

$D \arccot x = -{1 \over 1+x^2}$

• Eksponenttifunktioiden ja logaritmifunktioiden derivaatat

$D e^x = e^x\,$

$D a^x = a^x \ln a\,$, missä $a > 0\,$

$D \ln |x| = {1 \over x}$

$D \log_{a} |x| = {1 \over x \ln a}$, missä $a > 0\,$ ja $a \ne 1$

• Hyperbolisten funktioiden ja niiden käänteisfunktioiden derivaattoja

$D \sinh x = \cosh x\,$

$D \cosh x = \sinh x\,$

$D \tanh x = \frac{1}{\cosh^2 x}\,$

$D\ \operatorname{arsinh}\,x = { 1 \over \sqrt{x^2 + 1}}$

$D\ \operatorname{arcosh}\,x = { 1 \over \sqrt{x^2 - 1}}$

$D\ \operatorname{artanh}\,x = { 1 \over 1 - x^2}$

Todistuksia

Vakiofunktio

Olkoon $f(x)=c$, missä $c$ on vakio. Tämän derivaatta on määritelmän mukaan $Dc = \lim_{h\to 0}\frac{f(x+h)-f(x)}{h} = \lim_{h\to 0} \frac{c-c}{h} = 0$

Jolloin vakion derivoimissääntö on todistettu.

Potenssifunktio

Määritelmän mukaan

$D f(x) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h}$.

Potenssifunktiolle saadaan siten

$D x^n = \lim_{h \to 0} \frac{(x+h)^n - x^n}{h}$.

Edelleen tiedetään, että $(x+h)^n\,$ on muotoa

$a_0x^n + a_1 hx^{n-1} + a_2 h^2x^{n-2} + a_3 h^3x^{n-3} + ... + a_{n-1}h^{n-1}x + h^n\,$,

missä $a_i$ vastaa kunkin termin binomikerrointa. Tiedetään myös, että ensimmäinen binomikerroin $a_0 = 1\,$ ja toinen binomikerroin on $a_1 = n\,$. Saadaan siis

$\begin{matrix} \lim_{h \to 0} \frac{(x+h)^n - x^n}{h} & = & \lim_{h \to 0} \frac{a_0x^n + a_1 hx^{n-1} + a_2 h^2x^{n-2} + a_3 h^3x^{n-3} + ... + a_{n-1}h^{n-1}x + h^n - x^n}{h} \\ \\ & \ = & \lim_{h \to 0} \frac{n hx^{n-1} + a_2 h^2x^{n-2} + a_3 h^3x^{n-3} + ... + a_{n-1}h^{n-1}x + h^n}{h} \\ \\ & \ = & nx^{n-1}. \\ \\ \end{matrix}$

Tämän todistuksen ja summaussäännön perusteella voidaan helposti todistaa polynomifunktion $\sum_{k=0}^n a_kx^k$ derivaatta.

Sovelluksia

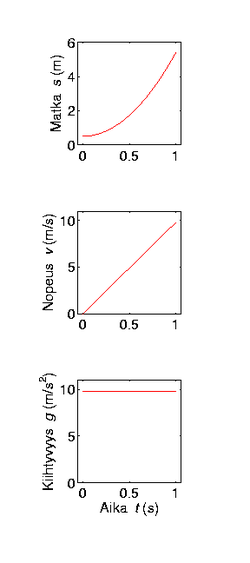
Derivointi on hyödyllinen matemaattinen apuneuvo myös teknisissä tieteissä. Seuraavassa yksinkertainen esimerkki derivaatan käytöstä fysiikassa. Oletetaan, että halutaan selvittää vaikkapa putoamiskiihtyvyys $g\,$, kun mitataan putoavan pallon putoama matka $s\,$ ajan $t\,$ funktiona. Tiedetään, että matka voidaan ilmaista

$s = s_{0} + \frac{1}{2}g t^{2}, \,$

ja nopeus $v\,$ on matkan derivaatta ajan suhteen

$v = \frac{ds}{dt} = \frac{d}{dt}\left(s_{0} + \frac{1}{2}g t^{2}\right) = \frac{1}{2}g\ 2 t = gt,$

mistä edelleen kiihtyvyys $g\,$ on nopeuden derivaatta ajan suhteen. Toisin sanoen siis matkan toinen derivaatta:

$\frac{d^{2}s}{d t} = \frac{d v}{d t} = \frac{d}{dt}\left(gt\right) = g.\$

Kun mitattu etäisyys derivoidaan ajan suhteen numeerisesti, saadaan kiihtyvyys. Ajan suhteen derivoitaessa saatetaan joskus myös käyttää derivaatan merkkinä pistettä derivoitavan suureen päällä $\frac{dx}{dt} = \dot x$ ja $\frac{d^{2}x}{dt} = \ddot x$.

Katso myös

• Osittaisderivaatta
• Integraalifunktio
• Jatkuva funktio
• Gradientti

Aiheesta muualla

• Opetus.tv: Matematiikan etäopiskeluympäristö, Derivaatta