Suurten lukujen laki

Suurten lukujen laki on todennäköisyyslaskennan tulos, joiden mukaan sellaisten satunnaismuuttujien jonon keskiarvo, joilla on sama odotusarvo, voidaan tietyin edellytyksin ja tietyssä mielessä sanoa suppenevan kohti niiden odotusarvoa, kun satunnaismuuttujien lukumäärä kasvaa rajatta. Erityisesti toistokokeessa, jossa tietty tulos saadaan joka kerta yhtä suurella todennäköisyydellä, tällaisten tulosten suhteellinen osuus kaikista koetuloksista lähestyy tämän todennäköisyyden osoittamaa lukua, kun toistojen lukumäärä kasvaa.
Suurten lukujen lailla on suuri käytännöllinen merkitys, koska se käytännössä "takaa", että satunnaisten ilmiöiden esiintymistiheys pitkällä aikavälillä voidaan ennustaa. Esimerkiksi vaikka pelikasino voikin menettää rahaa jollakin kerralla, kun rulettia pelataan, suurella määrällä pelikertoja sen kokonaisvoitto voidaan kutakuinkin varmasti ennustaa. Niinpä jollekulle pelaajalle maksettavan voiton korvaavat kasinon pitäjän kannalta käytännössä varmuudella muiden pelaajien maksamat pelimaksut. Yhdessä keskeisen raja-arvolauseen kanssa suurten lukujen laki muodostaakin perustan koko matemaattiselle tilastotieteelle.[1]
Nimensä mukaisesti suurten lukujen laki kuitenkin pätee vasta, kun käsitellään suurta määrää havaintoja. Ei ole olemassa sellaista säännönmukaisuutta, jonka mukaan jo pienellä määrällä havaintoja tulosten keskiarvon pitäisi vastata kunkin kerran odotusarvoa tai että satunnaista poikkeamaa keskiarvosta pitäisi välittömästi seuraavan kerran tuloksen "tasapainottaa". Virheellistä kuvitelmaa, että sellainen säännönmukaisuus olisi olemassa, sanotaan pelurin virhepäätelmäksi.
Esimerkkejä[muokkaa | muokkaa wikitekstiä]
Esimerkiksi heitettäessä tavallista kuusisivuista noppaa yhden kerran saadaan jokin luvuista 1, 2, 3, 4, 5 tai 6, jokainen yhtä suurella todennäköisyydellä (edellyttäen ettei noppa ole "painotettu"). Näin ollen nopanheiton tuloksen odotusarvo on
Suurten lukujen laista seuraa, että jos noppaa heitetään hyvin monta kertaa, heittojen tulosten keskiarvo on todennäköisesti lähellä lukua 3,5, sitä tarkemmin, mitä useampia kertoja noppaa heitetään.
Suurten lukujen laista seuraa, että onnistuminen empiirinen todennäköisyys sarjassa Bernoullin kokeita suppenee kohti teoreettista todennäköisyyttä. Bernoullin satunnaismuuttujan odotusarvo on sama kuin onnistuminen teoreettinen todennäköisyys, ja kun sellaisia satunnaismuuttujia on n kappaletta ja ne ovat riippumattomat ja identtisesti jakautuneet, niiden keskiarvo lähestyy tätä arvoa.
Esimerkiksi kolikon heittäminen on Bernoullin koe. Kun "painottamatonta" kolikkoa heitetään kerran, teoreettinen todennäköisyys saada kruuna on 1/2. Niinpä suurten lukujen lain mukaan suuressa määrässä kolikonheittoja kruunien suhteellisuuden osuuden pitäisi olla noin 1/2. Erityisesti kruunien osuus n heiton jälkeen suppenee melkein varmasti kohti arvoa 1/2, kun n kasvaa rajatta.
Vaikka kruunien ja myös klaavojen suhteellinen osuus lähestyy arvoa 1/2, samoin ei ole kruunien ja klaavojen lukumäärän erotuksen laita. Päin vastoin, se kasvaa itseisarvoltaan melkein varmasti. Toisin sanoen todennäköisyys sille, että näiden lukumäärien erotus olisi itseisarvoltaan tietyn rajan alapuolella, lähestyy nollaa heittojen lukumäärän kasvaessa. Melkein varmasti myös tämän erotuksen suhde heittojen lukumäärään lähestyy nollaa. Tämä lukumäärien erotus kasvaa kuitenkin hitaammin kuin kaikkien heittojen lukumäärä.
Historia[muokkaa | muokkaa wikitekstiä]
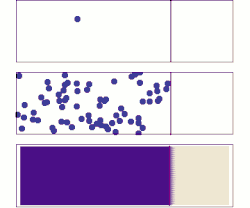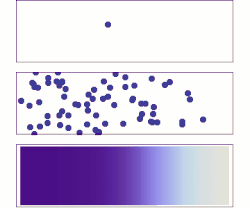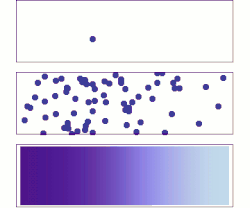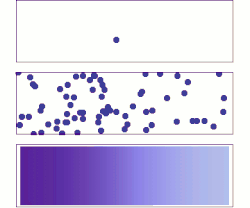
Ylhäällä: Yhden molekyylin liike näyttää täysin sattumanvaraiselta.
Keskellä: Muutaman molekyylin tapauksessa liuoksella on jo taipumus täyttää koko säiliö vähitellen yhä tasaisemmin, mutta esiintyy myös satunnaisia fluktuaatioita.
Alhaalla: Kun liuenneita molekyylejä on hyvin paljon eivätkä ne näy erikseen, satunnaisuutta ei näytä enää esiintyvän, vaan liuennut aine näyttää liikkuvan tasaisesti ja systemaattisesti sieltä, missä sen pitoisuus on suuri, sinne, missä sen pitoisuus ennestään on pieni. Käytännössä diffuusiota voidaankin käsitellä deterministisenä makroskooppisena ilmiönä (Fickin laki), vaikka se molekyylitasolla onkin luonteeltaan satunnaisilmiö.
Italialainen matemaatikko Gerolamo Cardano (1501–1576) väitti ilman todistusta, että empiiristen tilastojen pätevyydellä on taipumus kasvaa otoskoon kasvaessa.[2] Tämä väite muotoiltiin sittemmin suurten lukujen laiksi. Jakob Bernoulli todisti suurten lukujen lain erikoistapauksessa, joka koskee kaksiarvoisia satunnaismuuttujia.[3] Häneltä kesti yli 20 vuotta kehittää väitteelle riittävän täsmällinen matemaattinen todistus, jonka hän julkaisi teoksessaan Ars Conjectandi vuonna 1713. Hän nimitti sitä "kultaiseksi teoreemaksi", mutta nykyisin se tunnetaan Bernoullin lauseena. (Sitä ei pidä sekoittaa Jakob Bernoullin veljenpojan, Daniel Bernoullin mukaan nimettyyn Bernoullin lakiin fysiikassa.) Vuonna 1837 S. D. Poisson kuvaili tulosta tarkemmin ja antoi sille nimen "suurten lukujen laki" (ransk. Loi des grands nombres).[4][5] Tämän jälkeen tulos tunnettiin molemmilla nimillä, mutta "suurten lukujen laki" on yleisemmin käytetty.[6]
Bernoullin ja Poissonin todistettua tuloksensa muut matemaatikot kuten Pafnuti Tšebyšov [7], Markov, Borel, Cantelli ja Kolmogorov kehittivät vahvempia tuloksia, kunnes lopulta Aleksandr Khintšin lopulta esitti suurten lukujen laille todistuksen, joka pätee mielivaltaisille satunnaismuuttujille.[8] Nämä myöhemmät tutkimukset ovat johtaneet ennen kaikkea kahteen huomattavaan suurten lukujen lain muotoiluun. Toista sanotaan "heikoksi", toista "vahvaksi" laiksi, mitkä viittaavat kahteen erilaiseen tilastollisen suppenemisen muotoon. Kuten jäljempänä osoitetaan, heikko laki on samalla vahvan lain looginen seuraus.[8]
Muotoilut[muokkaa | muokkaa wikitekstiä]
Seuraavassa käsitellään lähinnä kahta suurten lukujen lain muotoilua, heikkoa ja vahvaa suurten lukujen lakia, sekä heikon lain erikoistapauksena myös Bernoullin lausetta. Lisäksi mainitaan uniforminen suurten lukujen laki ja Borelin suurten lukujen laki.
Lain kaikki versiot ilmaisevat matemaattisesti eri tavoin täsmennettynä periaatteen, että otoksen
keskiarvo suppenee suurella todennäköisyydellä kohti odotusarvoa
kun X1, X2, ... on päättymätön jono riippumattomia ja samoin jakautuneita satunnaismuuttujia, joiden odotusarvo on E(X1 = E(X2) = ...= µ. Oletetaan, että funktiot Xj ovat integroituvia Lebesguen mielessä, jolloin satunnaismuuttujilla on odotusarvo ja se on äärellinen.
Sen sijaan suurten lukujen laki ei välttämättä edellytä, että näillä satunnaismuuttujilla on myös äärellinen varianssi Var(X1) = Var(X2) = ... = σ2 < ∞. Hyvin suuri tai ääretön varianssi tekee suppenemisen hitaaksi, mutta suurten lukujen laki silti pätee. Tämä oletus kuitenkin usein tehdään, koska todistus on silloin helpompi ja lyhempi.
Vahva ja heikko laki eroavat toisistaan siinä, mitä suppenemisen tilastollisessa mielessä katsotaan merkitsevän.
Heikko suurten lukujen laki[muokkaa | muokkaa wikitekstiä]

Heikko suurten lukujen laki eli Khintšinin laki sanoo, että otoksen keskiarvo konvergoi stokastisesti kohti odotusarvoa. Jos X1, X2, ... Xi on joukko pareittain riippumattomia, samoin jakautuneita satunnaismuuttujia, joilla on sama odotusarvo EXi = μ ja varianssi D2Xi = σ2 ja niiden keskiarvolle käytetään merkintää , niin[9]
Tämä merkitsee, että jokaiselle positiiviselle luvulle ε pätee:
Tulos merkitsee oleellisesti, että valittiinpa mielivaltainen kuinka pieni positiivinen reaaliluku tahansa tarpeeksi suurella otoksella todennäköisyys, että havaintojen keskiarvo poikkeaa odotusarvosta enemmän kuin tämän luvun verran eli jää sen välin ulkopuolelle, joka ulottuu odotusarvosta kyseisen luvun verran kumpaankin suuntaan, lähestyy nollaa.
Tätä stokastista konvergenssia[9] eli suppenemista in probability (i.p.) sanotaan myös satunnaismuuttujan heikoksi konvergenssiksi. Tätä suurten lukujen lain muotoa sanotaan heikoksi, koska satunnaismuuttujat voivat supeta heikosti (in probability) tässä selitetyllä tavalla, vaikka ne eivät suppenisikaan vahvasti (melkein varmasti) jäljempänä selitetyllä tavalla.
Bernoullin lause[muokkaa | muokkaa wikitekstiä]
Bernoullin lause on suurten lukujen lain kauimmin tunnettu muoto ja itse asiassa heikon suurten lukujen lain erikoistapaus. Se koskee toistokokeita, joissa on vain kaksi mahdollista tulosta: jokin "suotuisa" tulos joko saadaan tai ei. Bernoullin lause sanoo, että jos tällainen koe suoritetaan n kertaa ja joka kerta tämä suotuista tulos tietyllä todennäköisyydellä p, toistokertojen lukumäärän kasvaessa todennäköisyys, että sellaisten kertojen suhteellinen osuus, jolloin tämä tulos saadaan, poikkeaa p:stä enemmän kuin annetun vakion ε verran, lähestyy nollaa. Toisin sanoen:[10]
Tällaisen toistokokeen suorituskerta voidaan nimittäin käsittää diskreetiksi, Bernoullin jakaumaa noudattavaksi satunnaismuuttujaksi, joka voi saada vain kahta arvoa. Jos toista niistä merkitään luvulla 1, toista luvulla 0, ja arvo 1 saadaan joka kerta todennäköisyydellä p, tämän satunnaismuuttujan odotusarvo on p.
Vahva suurten lukujen laki[muokkaa | muokkaa wikitekstiä]
Vahva suurten lukujen laki sanoo, että samoilla ehdoilla otoksen keskiarvo suppenee melkein varmasti (engl. almost surely, lyh. a.s.) kohti odotusarvoa. Jos X1, X2, ... Xi on joukko pareittain riippumattomia, samoin jakautuneita satunnaismuuttujia, joilla on sama odotusarvo EXi = μ ja varianssi D2Xi = σ2 ja niiden keskiarvolle käytetään merkintää , niin[9]
Toisin sanoen jono {Xn} suppenee perusjoukon jokaisella alkeistapauksella lukuun ottamatta mahdollisesti tapahtumaa, jonka todennäköisyys on nolla[9], eli
Tämän todistus on monimutkaisempi kuin heikon lain.[11] Laki oikeuttaa (Lebesguen mielessä integroituvien) satunnaismuuttujien tapauksessa odotusarvon intuitiivisen tulkinnan "pitkän aikavälin keskiarvona."
Melkein varmaa konvergenssia sanotaan myös satunnaismuuttujan vahvaksi konvergenssiksi. Tätä versiota sanotaan "vahvaksi laiksi", koska jokainen satunnaismuuttujien joukko, joka suppenee vahvasti (melkein varmasti), suppenee myös heikosti (in probablity). Vahvasta laista seuraakin heikko laki, mutta ei päin vastoin. Kun vahvan lain edellytykset täyttyvät, satunnaismuuttuja suppenee sekä vahvasti (melkein varmasti) että heikosti (in probability).
Matemaatikkojen keskuudessa on esitetty näkemyksiä, että molemmat lait olisi yhdistettävä ja että heikolla suurten lukujen lailla sellaisenaan on vain vähän mielenkiintoa.[12] Molemmille laeille on kuitenkin olemassa yleistyksiä, jotka osoittavat niiden pätevän tietyillä edellä esitettyjä yleisemmilläkin edellytyksillä. On sellaisiakin tapauksia, joissa heikon lain tulos pätee, mutta vahvan ei.
Vahvan suurten lukujen lain laajin yleistys on Kolmogorovin lause, joka on samalla välttämätön ehto satunnaismuuttujien keskiarvon melkein varmalle kongervenssille. Jos X1, X2, ... Xi on joukko pareittain riippumattomia, samoin jakautuneita satunnaismuuttujia, joilla on sama odotusarvo EXi = μ, niin
- ,
jos ja vain jos odotusarvo EXi = μ on olemassa.[9]
Erot vahvan ja heikon lain välillä[muokkaa | muokkaa wikitekstiä]
Heikko laki sanoo, että annetulle suurelle luvulle n keskiarvo on todennäköisesti lähellä arvoa μ Se jättää siis avoimeksi, voiko tapahtuma, jossa , sattua vaikka äärettömän monta kertaa, joskin pitkin väliajoin.
Vahva laki osoittaa, että niin melkein varmasti ei tapahdu. Erityisesti siitä seuraa, että todennäköisyydellä 1 jokaiselle ε > 0 epäyhtälö pätee kaikilla riittävän suurilla arvoilla n.[13]
Seuraavissa tapauksissa vahva suurten lukujen laki ei päde, heikko laki kylläkin. [14][15][16]
1. Olkoon x eksponenttijakautunut satunnaismuuttuja parametrin arvolla 1. Silloin siitä johdetun satunnaismuuttujan : odotusarvo on
2. Olkoon x geometrisesti jakautunut satunnaismuuttuja parametrin arvolla 0,5. Silloin on
3.
Uniforminen suurten lukujen laki[muokkaa | muokkaa wikitekstiä]
Olkoon f(x,θ) jokin joukossa Θ määritelty jatkuva funktio. Olkoon lisäksi jokaisella arvolla jono {f(X1,θ), f(X2,θ), …} sellainen jono riippumattomia ja samoin jakautuneita satunnaismuuttujia, että tämä jono konvergoi stokastisesti (in probability) kohti arvoa to E[f(X,θ)]. Tällaista sanotaan pisteittäiseksi konvergenssiksi Θ:ssa.
Uniforminen suurten lukujen laki osoittaa ehdot, joilla tämä suppeneminen tapahtuu tasaisesti joukossa Θ. Jos [19] [20]
- Θ on kompakti,
- f(x,Θ) on jatkuva jokaisessa pisteessä
melkein kaikilla arvoilla x ja se on jokaisella θ:n arvolla x:n mitallinen funktio
- on olemassa sellainen dominoiva funktio d(x), että E[d(X)] < ∞, ja
Silloin E[f(X,θ)] on jatkuva joukossa Θ, ja
Tulos on käyttökelpoinen laajojen estimaattorien luokan johtamisessa.
Borelin suurten lukujen laki[muokkaa | muokkaa wikitekstiä]
Borelin suurten lukujen laki, joka on nimetty Émile Borelin mukaan, sanoo, että jos jokin koe toistetaan suuri määrä kertoja, toisistaan riippumatta samanlaisissa olosuhteissa, niiden kertojen lukumäärä, jolloin tietty tapahtuma esiintyy, on likipitäen yhtä suuri kuin tapahtuman todennäköisyys kullakin kerralla; mitä suurempi toistojen lukumäärä on, sitä parempi likiarvo saadaan. Tarkemmin sanottuna, jos E merkitsee kyseistä tapahtumaa, p sen todennäköisyyttä ja Nn(E) niiden kertojen lukumäärää, joilla tapahtuma E sattuu n ensimmäisen toistokerran aikana, niin todennäköisyydellä 1 pätee:[21]
Tämä voidaan todistaa Tšebyšovin epäyhtälön avulla: Olkoon X satunnaismuuttuja, jolla on äärellinen odotusarvo μ ja äärellinen nollasta poikkeava varianssi σ2. Silloin jokaiselle reaaliluvulle k > 0 pätee
Tulos vahvistaa intuitiivisen käsityksen todennäköisyydestä tapahtuman esiintymisen pitkäaikaisena suhteellisena frekvenssinä. Se on erikoistapaus useista todennäköisyysteoriassa esiintyvistä yleisimmistä suurten lukujen lain versioista.
Todistus[muokkaa | muokkaa wikitekstiä]
Olkoon X1, X2, ... on päättymätön jono riippumattomia ja samoin jakautuneita satunnaismuuttujia, joiden odotusarvo on E(X1) = E(X2) = ... = μ < ∞. Tutkitaan otoksen keskiarvon
suppenemista. Heikko suurten laki merkitsee tällöin seuraavaa:
Todistus Tšebyšovin epäyhtälön avulla[muokkaa | muokkaa wikitekstiä]
Tämä todistus edellyttää, että satunnaismuuttujilla on äärellinen varianssi (kaikilla ). Satunnaismuuttujien riippumattomuus merkitsee, ettei niiden välillä ei ole korrelaatiota, ja tällöin on
Sarjan yhteinen keskiarvo μ on otoksen keskiarvon odotusarvo:
Soveltamalla Tšebyšovin epäyhtälöä keskiarvoon saadaan:
Tästä seuraa edelleen:
Kun n kasvaa rajatta, tämä lauseke lähestyy arvoa 1. Stokastisen konvergenssin (in probability) määritelmän mukaan tämä osoittaa, että
Todistus karakterististen funktioiden suppenemisen avulla[muokkaa | muokkaa wikitekstiä]
Kompleksifunktioita koskevan Taylorin lauseen mukaan minkä tahansa satunnaismuuttujan X karakteristinen funktio äärellisellä keskiarvolla μ voidaan kirjoittaa muotoon
Kaikilla satunnaismuuttujilla X1, X2, ... on sama karakteristinen funktio, joten käytetään sille yksinkertaisesti merkintää φX.
Karakteristisen funktion perusominaisuuksiin kuuluu, että
- jos X ja Y ovat riippumattomat.
Näiden sääntöjen avulla voidaan laskea keskiarvon karakteristinen funktio φX:n avula:
Raja-arvo eitμ on vakioarvoisen satunnaismuuttujan μ karakteristinen funktio, ja näin ollen Lévyn jatkuvuuslauseen mukaan lähestyy rajajakaumaa μ:
Tässä μ on vakio, mistä seuraa, että jakaumakonvergenssi kohti μ:tä ja stokastinen konvergenssi kohti μ:tä ovat yhtäpitäviä ominaisuuksia. Sen vuoksi
Tämä osoittaa, että otoksen keskiarvo konvergoi stokastisesti kohti karakteristisen funktion derivaattaa origoissa niin kauan kuin sellainen on olemassa.
Katso myös[muokkaa | muokkaa wikitekstiä]
Lähteet[muokkaa | muokkaa wikitekstiä]
- Hazewinkel, Michie: ”Law of Large Numbers”, Encyclopedia of Mathematics. Springer, 2001. ISBN 978-1-55608-4.
- Grimmett, G. R. & Stirzaker, D. R.: Probability and Random Processes, 2nd Edition. Oxford: Clarendon Press, 1992. ISBN 0-19-853665-8.
- Durrett, Richard: Probability: Theory and Examples, 2nd Edition. Duxbury Press, 1995.
- Jacobsen, Martin: Videregående Sandsynlighedsregning (Advanced Probability Theory) 3rd Edition. Kööpenhamina: HCØ-tryk, 1992. ISBN 87-91180-71-6.
- Loève, Michel: Probability theory 1, 4. painos. Springer Verlag, 1977.
- Newey, Whitney K. & McFadden, Daniel: Large sample estimation and hypothesis testing, s. 2111–2245. Elsevier Science, 1994.
- Ross, Sheldon: A first course in probability, 8. painos. Prentice Hall press, 2009. ISBN 978-0-13-603313-4.
Viitteet[muokkaa | muokkaa wikitekstiä]
- ↑ Pekka Tuominen, Pekka Norlamo: ”Alkusanat”, Todennäköisyyslaskenta, osa 1. Limes ry, 1978. ISBN 951-745-023-0.
- ↑ L. Mlodinow: The Drunkard's Walk, s. 50. New York: Randon House, 2008.
- ↑ Jakob Bernoulli: ”4. luku”, Ars Conjectandi: Usum & Applicationem Praecedentis Doctrinae in Civilibus, Moralibus & Oeconomicis. {{{Julkaisija}}}, 1713.
- ↑ S. D. Poisson: Probabilité des jugements en matière criminelle et en matière civile, précédées des règles générales de calcul des probabilités, s. 7 (todistukset sivuilla 139–143 ja 277). Pariisi: Bachelier, 1837. Teoksen verkkoversio.
- ↑ Ian Hacking: 19th-century Cracks in the Concept of Determinism. Journal of the History, 1983, 44. vsk, nro 3, s. 455-475. JSTOR 2709176.
- ↑ 19th-century Cracks in the Concept of Determinism. Journal of the History of Ideas, 1983, 44. vsk, nro 3, s. 455-475. JSTOR 2709176.
- ↑ Pafnuti Tšebyšov: Démonstration élémentaire d'une proposition générale de la théorie des probabilités. Journal für die reine und angewandte Mathematik (Crelles Journal), 1846, nro 33, s. 259–267. doi:10.1515/crll.1846.33.259.
- ↑ a b Eugene Seneta: A Tricentenary history of the Law of Large Numbers. Bernoulli, 2013, 19. vsk, nro 4, s. 1088–1121. doi:10.3150/12-BEJSP12. Artikkelin verkkoversio.
- ↑ a b c d e Pekka Tuominen, Pekka Norlamo: ”Suurten lukujen lait”, Todennäköisyyslaskenta, osa 2, s. 465–476. Limes ry, 1978. ISBN 951-745-023-0.
- ↑ Pekka Tuominen, Pekka Norlamo: ”Bernoullin lause”, Todennäköisyyslaskenta, osa 1, s. 95–97. Limes ry, 1978. ISBN 951-745-023-0.
- ↑ The strong law of large numbers « What’s new Terrytao.wordpress.com. Viitattu 5.1.2016.
- ↑ Oleg Kelsov: ”Comments”, Limit Theorems for Multi-Indexed Sums of Random Variables, s. 219. Springer, 2014. ISBN 9783-662-44387-3. Teoksen verkkoversio.
- ↑ Sheldon Ross: A first course in probability (8. painos). Prentice Hall, 2009. ISBN 978-0-13-603313-4.
- ↑ Erich L. Lechmann, Joseph P. Romano: ”Weak law converges to constant”, Testing Statistical Hypotheses, s. 432. Springer, 2006. ISBN 9780387276052. Teoksen verkkoversio.
- ↑ A NOTE ON THE WEAK LAW OF LARGE NUMBERS FOR EXCHANGEABLE RANDOM VARIABLES Dguvl Hun Hong, Sung Ho Lee.
- ↑ weak law of large numbers: proof using characteristic functions vs proof using truncation VARIABLES math.stackexchange.com.
- ↑ Sayn Mukherjee: Law of large numbers isds.duke.edu. Arkistoitu 9.3.2013. Viitattu 5.1.2016.
- ↑ Law of large numbers stat.umn.edu.
- ↑ Whitney K. Newey, Daniel McFadden: ”Large sample estimation and hypothesis testing, ch. 3”, Handbook of Econometrics, s. 2111–2245. Elsevier Science, 1994.
- ↑ Robert I. Jennrich, Otsikko = Asymptotic Properties of Non-Linear Least Squares Estimators: The Annals of Mathematical Statistics, 1969, 40. vsk, nro 2, s. 633–643. doi:10.1214.
- ↑ L. Wen: An Analytic Technique to Prove Borel's Strong Law of Large Numbers. Am Math Month, 2001. Artikkelin verkkoversio.
Aiheesta muualla[muokkaa | muokkaa wikitekstiä]
- Weak Law of Large Numbers Wolfram MathWorld. Viitattu 5.1.2016.
- Strong Law of Large Numbers Wolfram MathWorld. Viitattu 5.1.2016.
- Kiersz, Andy: Apple CEO Tim Cook said something that would make statisticians cringe. Business Insider UK, 11.2.2015. Business Insider.


















![{\displaystyle \sup _{\theta \in \Theta }\left\|{\frac {1}{n}}\sum _{i=1}^{n}f(X_{i},\theta )-\operatorname {E} [f(X,\theta )]\right\|{\xrightarrow {\mathrm {a.s.} }}\ 0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/78c443ebcfe639a67acfbbf0c735a4f0462ff1e9)













![{\displaystyle \varphi _{{\overline {X}}_{n}}(t)=\left[\varphi _{X}\left({t \over n}\right)\right]^{n}=\left[1+i\mu {t \over n}+o\left({t \over n}\right)\right]^{n}\,\rightarrow \,e^{it\mu },\quad {\text{as}}\quad n\rightarrow \infty .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9dd13186d9c12e9a080c9d59c67ef07ad99159af)



