Pii (vakio)

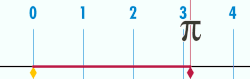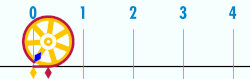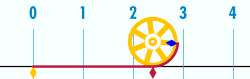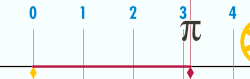
Kun ympyrän halkaisija on 1, ympyrän kehä on pii.

Luku pii (merkitään pienellä kreikkalaisella π-kirjaimella) on matemaattinen vakio, joka esiintyy monilla matematiikan ja fysiikan alueilla. Se tunnetaan myös nimillä Arkhimedeen vakio ja (erityisesti saksankielisellä alueella) Ludolfin luku.

Piin likiarvo katkaistuna 50 desimaalin jälkeen on 3,14159265358979323846264338327950288419716939937510.

Määritelmän mukaan pii on yhtä kuin ympyrän kehän suhde halkaisijaan (euklidisessa geometriassa). Vaihtoehtoisesti pii voidaan määritellä r-säteisen ympyrän pinta-alan suhteena r-sivuisen neliön pinta-alaan: $\frac{\pi r^2}{r^2} = \pi$. Joissain analyysin kirjoissa pii määritellään pienimmäksi positiiviseksi luvuksi x, jolle sin(x) = 0.

Eukleideen Alkeet-teoksen luvussa XII todistetaan, että kahden ympyrän alan suhde on sama kuin niiden halkaisijoiden neliöiden suhde. Tästä seuraa, että ympyrän pinta-ala on vakio (= π / 4) kertaa sen halkaisijan neliö. Pii on irrationaaliluku eli luku, jonka desimaalikehitelmä on päättymätön ja jaksoton. Ferdinand Lindemann todisti vuonna 1882 piin olevan transsendenttiluku, eli luku, joka ei ole minkään rationaalilukukertoimisen polynomin nollakohta.

Piin historia

Koska pii on transsendenttiluku, sitä ei voi esittää päättyvänä lausekkeena peruslaskutoimituksia, potenssiinkorotusta ja juurenottoa käyttäen. Sitä on kuitenkin kauan arvioitu likimääräisesti. Vanhan testamentin Kuningasten kirjassa π on 3: "Hiram valoi myös pyöreän altaan, jota kutsuttiin mereksi. Se oli reunasta reunaan kymmenen kyynärän levyinen, korkeutta sillä oli viisi kyynärää, ja vasta kolmenkymmenen kyynärän pituinen mittanuora ulottui sen ympäri". (Tätä selkeää virhettä on selitetty sillä, että halkaisijan arvona on käytetty astian sisämittaa.)

Ensimmäisiä säällisiä säilyneitä π:n likiarvoja on egyptiläisen matemaatikko Ahmosen käyttämä. Se on säilynyt laskutehtävissä, jotka sisältyvät niin sanottuun Rhindin papyrukseen. Sen mukaan ympyrän pinta-ala on yhtä suuri kuin sellaisen neliön, jonka sivu on 8/9 ympyrän halkaisijasta. Tämä vastaa π:n likiarvoa 256/81 eli noin 3,16. Noin 2000 vuotta ennen ajanlaskun alkua babylonialaiset otaksuivat, että π on joko 3 tai $\frac{25}{8}$. Myös likiarvo $\frac{22}{7}$ on tiedetty pitkään.

Kreikkalainen filosofi ja matemaatikko Arkhimedes todisti ympyrän sisään ja ympärille piirrettyjen monikulmioiden avulla, että ympyrän kehän ja halkaisijan suhde on lukujen $3 \frac{1}{7}$ ja $3 \frac{10}{71}$ välillä. Ptolemaios käytti π:n arvoa $\frac{377}{120}$. Kiinalainen Tsi Ch'ung-Chi löysi 400-luvulla π:lle arvon $\frac{355}{113}$, jota parempi murtolukuarvio on vasta $\frac{103993}{33102}$.

Luku π todistettiin irrationaaliluvuksi 1700-luvulla.

Sarjakehitelmät

Piin voi esittää päättymättömänä sarjana. Eräs varhainen ja yksinkertainen tapa määritellä pii sarjana on Gottfried Leibnizin kehittämä Gregory–Leibniz-sarja:

$\pi = \frac{4}{1}-\frac{4}{3}+\frac{4}{5}-\frac{4}{7}+\frac{4}{9}-\frac{4}{11}\cdots\,$

Tämä sarja suppenee kuitenkin liian hitaasti, jotta sitä kannattaisi käyttää piin likiarvojen laskemiseen. Siitä olisi laskettava vähintään 294 ensimmäistä termiä, jotta saataisiin edes kaksidesimaalinen likiarvo 3,14. Vuonna 1706 John Machin todisti kuitenkin seuraavan yhtälön:

$\frac{\pi}{4} = 4 \, \arctan \frac{1}{5} - \arctan \frac{1}{239}\!$

Koska arkustangentin Taylorin sarjakehitelmä on

$\arctan \, x = x - \frac{x^3}{3} + \frac{x^5}{5} - \frac{x^7}{7} + \cdots\!$

saatiin tästä piille nopeasti suppeneva ja käyttökelpoinen sarjakehitelmä:

$\frac{\pi}{4} = \frac{4}{5} - \frac{4}{3 \cdot 5^3} + \frac{4}{5 \cdot 5^5} - \frac{4}{7 \cdot 5^7} + .... - \frac{1}{239} + \frac{1}{3 \cdot 239^3} - \frac{1}{5 \cdot 239^5} + \frac{1}{7 \cdot 239^7} - ...$

Machin itse laski tällä kaavalla piin 100 desimaalin tarkkuudella, ja myöhemminkin tätä sarjaa on paljon käytetty yhä tarkempien likiarvojen laskemiseen.

Piin desimaalien laskeminen

Englantilainen matemaatikko William Shanks laski 20 vuoden ajan piin desimaaleja käsin ja ratkaisi luvun 707 desimaalin tarkkuudella. Vuonna 1945 kuitenkin huomattiin, että laskun 528. desimaali oli laskettu virheellisesti.

Nykyään piin desimaaleja lasketaan tietokoneilla.

1900-luvulla pii tunnettiin jo yli miljardin desimaalin tarkkuudella, ja nykyään siitä tiedetään ensimmäiset noin 2,5 biljoonaa desimaalia. 1990-luvulla kehitettiin tapoja laskea piin heksadesimaaliesityksen numeroita mielivaltaisesta kohdasta ilman, että aiempia numeroita tarvitsee tietää.

Avoimia kysymyksiä

Vaikka piistä tiedetään paljon, on vielä useita avoimia kysymyksiä sen desimaaleihin liittyen:

• Onko desimaaleissa toistuvia kuvioita, vai onko ketju hahmoton?
• Toistuvatko jotkut numerot tai luvut piissä useammin kuin toiset?

Katso myös

• Luettelo piin laskukaavoista

Lähteet

• Theoni Pappas: Lisää matematiikan iloja. (Alkuteos: More Joy of Mathematics. Exploring Mathematics All Around You). Suom. Juha Pietiläinen. Helsinki: Terra Cognita, 1991. ISBN 952-5202-46-1.

Kirjallisuutta

• Beckmann, Petr: π: Erään luvun tarina. (A history of π, 1971.) Suomentanut Hannele Salminen. Helsinki: Terra Cognita, 2000. ISBN 952-5202-28-3.

Aiheesta muualla

• [2] Gutenberg-projektin teksti, jossa on ensimmäiset 10 miljoonaa desimaalia
• PiFastilla voi itse laskea piin ja muiden vakioiden arvoja erittäin tarkasti
• Pi-memory
• [3] Pii-laskin, joka toimii selaimessa