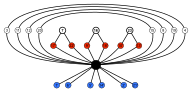
Oktaedrinen symmetria

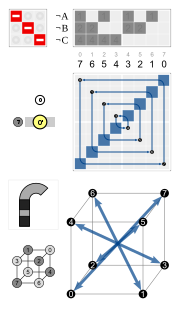
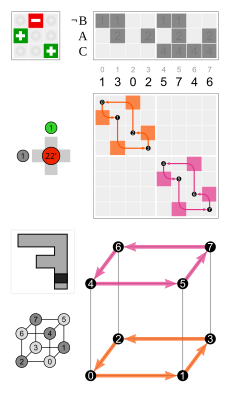
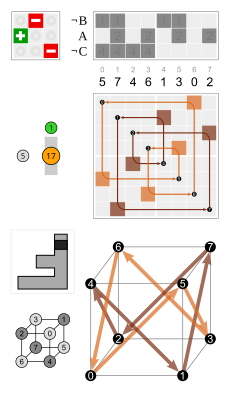
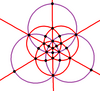
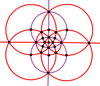
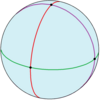
Neljällä kuusikulmaisella syklillä on yhteinen inversio (musta solmu huipulla). Kuusikulmiot ovat symmetriset niin, että esimerkiksi 3 ja 4 ovat samalla syklillä, mutta 3 ja 12 eivät.
Oktaedrinen symmetria on sellaisen kolmiulotteisen kappaleen symmetria, joka säännöllisen oktaedrin tavoin voidaan kuvata itselleen isometrisesti 48 tavalla, joista 24 on orientaation säilyttäviä. Oktaedrin ohella myös kuutiolla on oktaedrinen symmetria, sillä se on oktaedrin duaalikappale.
Oktaedrisesti symmetrisen kappaleen orientaation säilyttävien symmetriaoperaatioiden ryhmä on S4, sama kuin neljän alkion permutaatioryhmä, sillä oktaedrin vastakkaiset sivut muodostavat neljä paria ja jokaista tällaista symmetriaoperaatiota vastaa yksi näiden parien permutaatio.
Ominaisuuksia
[muokkaa | muokkaa wikitekstiä]Diskreeteistä pistesymmetrioista sekä myös pallopinnan symmetrioista kiraalinen ja täysi (eli akiraalinen) oktaedrinen symmetria Kiraalisella ja täydellä (eli akiraalisella) oktaedrisella symmetrialla on suurin symmetriaryhmä kaikista sellaista diskreetin pistejoukon symmetrioista ja samalla myös pallopinnan symmetrioista jotka ovat yhteensopivia siirtosymmetrian kanssa. Ne kuuluvat kuutiollisen kidejärjestelmän kristallografisiin pisteryhmiin.
| O:n alkiot | O:n alkioiden inversiot | ||
|---|---|---|---|
| identtinen kuvaus | 0 | inversio | 0' |
| 3 × 180°:n rotaatio nelinkertaisen akselin ympäri | 7, 16, 23 | 3 × peilaus nelinkertaista akselia vastaan kohtisuorassa olevan tason suhteen | 7', 16', 23' |
| 8 × 120°:n rotaatio kolminkertaisen akselin ympäri | 3, 4, 8, 11, 12, 15, 19, 20 | 8 × 60°:n rotaation ja peilauksen yhdistetty kuvaus | 3', 4', 8', 11', 12', 15', 19', 20' |
| 6 × 180°:n rotaatio kaksinkertaisen akselin ympäri | 1', 2', 5', 6', 14', 21' | 6 × peilaus kaksinkertaista akselia astaan kohtisuorassa olevan tason suhteen | 1, 2, 5, 6, 14, 21 |
| 6 × 90°:n rotaatio nelinkertaisen akselin ympäri | 9', 10', 13', 17', 18', 22' | 6 × 90°:n rotaation ja peilauksen yhdistetty kuvaus | 9, 10, 13, 17, 18, 22 |
| Esimerkkejä | ||||
|---|---|---|---|---|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Täysi oktaedrinen ryhmä on kolmiulotteinen hyperoktaedraalinen ryhmä. Sellaisena se on samalla yhteenpunottu tulo (wreath product) ,
, ja sen alkiot voidaan luonnollisella tavalla määritellä pareina , missä ja .
Lisäksi se on samalla suora summa , ja sen tetraedrisen aliryhmän Td alkiot voidaan yksinkertaisesti samastaa lukujen kanssa ja niiden inversiot esittää luvuilla .
Niinpä esimerkiksi identtinen kuvaus voidaan esittää muodossa ja inversio muodossa .
Alkiota esittää luku ja alkiota merkintä .
Rotaation ja peilauksen yhdistettyä kuvausta sanotaan rotorefleksioksi.
| rotorefleksion havainnollistus | ||||
|---|---|---|---|---|
|
| ||||
|
| ||||
Kiraalinen oktaedrinen symmetria
[muokkaa | muokkaa wikitekstiä]| Pyörimisakselit | ||
|---|---|---|
| C4 |
C3 |
C2 |
| 3 | 4 | 6 |
O, 432 eli [4,3]+, kertaluokkaa 24, on kiraalinen oktaedrinen symmetria eli rotationaalinen oktaedrinen symmetria. Tämä ryhmä on muutoinen tetraedrisen symmetrian T kaltainen, mutta C2-akselit ovat nyt C4-akseleita ja lisäksi on kuusi C2-akselia, jotka kulkevat kuution särmien keskipisteiden kautta. Td ja O ovat isomorfisia abstrakteja ryhmiä: molemmat vastaavat ryhmää S4, neljän kohteen symmetriaryhmää. Td on T:n ja sen joukon unioni, joka saadaan yhdistämällä jokainen O \ T:n alkio inversiolla. O on kuution ja säännöllisen oktaedrin rotaatioryhmä.
| Ortogonaalinen projektio | Stereografinen projektio | ||
|---|---|---|---|
| 2:nkertainen | 4:nkertainen | 3:nkertainen | 2:nkertainen |

|

|

|

|
Täysi oktaedrinen symmetria
[muokkaa | muokkaa wikitekstiä]Täyden eli akiraalisen oktaedrisen symmetrian symmetriaryhmälle käytetään merkintöjä Oh, *432, [4,3] tai m3m, ja se on kertalukua 48. Sillä on samat rotaatioakselit kuin O:lla, mutta lisäksi symmetriatasot, niiden joukossa sekä Td:n että Th:n kanssa. Tämä ryhmä on isomorfinen S4.C2:n kanssa, ja se on kuution ja oktaedrin symmetriaryhmä. Se on hyperoktaedrinen ryhmä, kun n=3.
Symmetria-akseleista kolme on kohtisuorassa toisiaan vastaan, ja ne voidaan valita koordinaattiakseleiksi.. Tällöin Oh:n erään perusalueen määrittää epäyhtälöryhmä 0 < x < y < z. Kappaleen, jolla on tämä symmetria, määrittää se osa kappaleesta, joka on tässä perusalueessa, esimerkiksi kuution määrittää yhtälö z = 1 ja oktaedrin yhtälö x + y + z = 1 (tai vastaavat epäyhtälöt, jolloin saadaan koko kappale eikä vain sen rajapintaa.) Yhtälö ax + by + cz + 1 määrittää 48-sivuisen monitahokkaan, disdyakis-dodekaedrin.
Tahkot voidaan yhdistää laajemmiksi tahkoiksi yhtälöillä a + b = 0 (kuutio) ja a = b = c (oktaedri).
Täyden oktaedrisen symmetrian 9 symmetria-akselia voidaan jakaa kahteen aliryhmään, joista toisessa niitä on kolme, toisessa kuusi. Ne vastaavat kahta ortogonaalista alisymmetriaa: diedristä symmetriaa D2h ja tetraedrista symmetriaa T4.
| Oktaedrinen symmetria ja peilaukseen perustuvat aliryhmät | ||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
||||||||||||||||||||||||||||||||
Rotaatiomatriisit
[muokkaa | muokkaa wikitekstiä]Oktaedrisen symmetrian rotaatiomatriisit voidaan muodostaa lähtemällä kaikkien 3x3-permutaatiomatriisien joukosta. Tällaisia matriiseja on kolme, ja niistä kussakin luku 1 esiintyy kolme kertaa. Varustetaan nämä ykköset joko etumerkillä + tai -. Tällä tavoin saadaan kaikkiaan 48 matriisia, jotka yhdessä muodostavat täyden oktaedrisen ryhmän. Niistä 24:lla on determinantin arvona +1 ja toisilla 24:llä -1. Näistä edelliset ovat kiraalisen oktaedrisen ryhmän rotaatiomatriiseja, jälkimmäiset 24 taas vastaavat peilauksia ja inversioita.
Oktaedrinen symmetria saadaan myös lähtemällä kolmesta generaattorimatriisista, jotka kuvaavat peilauksia ja vastaavat kolmea peiliä Coxeterin-Dynkinin diagrammissa. Näiden heijastusten tuloina saadaan kolme rotationaalista generaattoria.
| Peilaukset | Rotaatio | |||||
|---|---|---|---|---|---|---|
| Name | R0 | R1 | R2 | R0R1 | R1R2 | R0R2 |
| Ryhmä | ||||||
| Kertaluku | 2 | 2 | 2 | 4 | 3 | 2 |
| Matriisi |
|
|
|
|
|
|
Täyden oktaedrisen symmetrian aliryhmät
[muokkaa | muokkaa wikitekstiä]|
O Td Th |
 |
|
Rotaatioaliryhmät Peilausaliryhmät Inversioita sisältävät aliryhmät |
| Schoenflies | Coxeter | Orb. | H-M | Rakenne | Sykl. | Kertaluku | Indeksi | |
|---|---|---|---|---|---|---|---|---|
| Oh | [4,3] | *432 | m3 | S4×S2 | 48 | 1 | ||
| Td | [3,3] | *332 | 43m | S4 | 24 | 2 | ||
| D4h | [2,4] | *224 | 4/mmm | Dih1×Dih4 | 16 | 3 | ||
| D2h | [2,2] | *222 | mmm | Dih13=Dih1×Dih2 | 8 | 6 | ||
| C4v | [4] | *44 | 4mm | Dih4 | 8 | 6 | ||
| C3v | [3] | *33 | 3m | Dih3=S3 | 6 | 8 | ||
| C2v | [2] | *22 | mm2 | Dih2 | 4 | 12 | ||
| Cs=C1v | [ ] | * | 2 tai m | Dih1 | 2 | 24 | ||
| Th | [3+,4] | 3*2 | m3 | A4×S2 | 24 | 2 | ||
| C4h | [4+,2] | 4* | 4/m | Z4×Dih1 | 8 | 6 | ||
| D3d | [2+,6] | 2*3 | 3m | Dih6=Z2×Dih3 | 12 | 4 | ||
| D2d | [2+,4] | 2*2 | 42m | Dih4 | 8 | 6 | ||
| C2h = D1d | [2+,2] | 2* | 2/m | Z2×Dih1 | 4 | 12 | ||
| S6 | [2+,6+] | 3× | 3 | Z6=Z2×Z3 | 6 | 8 | ||
| S4 | [2+,4+] | 2× | 8 | Z4 | 4 | 12 | ||
| S2 | [2+,2+] | × | 1 | S2 | 2 | 24 | ||
| O | [4,3]+ | 432 | 432 | S4 | 24 | 2 | ||
| T | [3,3]+ | 332 | 23 | A4 | 12 | 4 | ||
| D4 | [2,4]+ | 224 | 422 | Dih4 | 8 | 6 | ||
| D3 | [2,3]+ | 223 | 322 | Dih3=S3 | 6 | 8 | ||
| D2 | [2,2]+ | 222 | 222 | Dih2=Z22 | 4 | 12 | ||
| C4 | [4]+ | 44 | 4 | Z4 | 4 | 12 | ||
| C3 | [3]+ | 33 | 3 | Z3=A3 | 3 | 16 | ||
| C2 | [2]+ | 22 | 2 | Z2 | 2 | 24 | ||
| C1 | [ ]+ | 11 | 1 | Z1 | 1 | 48 | ||
|
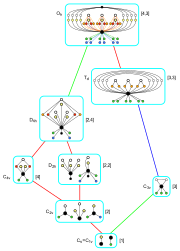
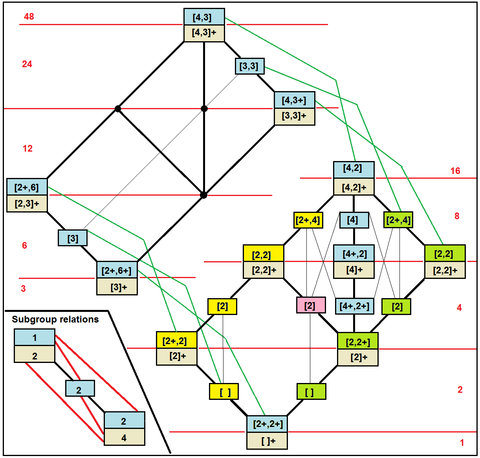
| Oktaedriset aliryhmät Coxeterin diagrammeilla esitettyinä[1] |
Kuution isometriat
[muokkaa | muokkaa wikitekstiä]
Kuutiolla on 48 isometriaa eli symmetria-alkiota, joiden muodostama symmetriaryhmä Oh on isomorfinen ryhmän S4 × C2 kanssa. Ne voidaan luokitella seuraavasti:
- O (identtinen kuvaus ja 23 aitoa rotaatiota), joilla on seuraavat konjugaattiluokat (suluissa avaruuslävistäjien permutaatiot ja kvaternioesitys):
- 1 kpl: identtinen kuvaus (1)
- 6 kpl: 90°:n rotaatiot kunkin tahkon keskipisteestä kuution keskipisteen kautta vastakkaisen tahkon keskipisteeseen kulkevan akselin ympäri: 3 akselia, 2 rotaatiota akselia kohti, yhteensä 6 ((1 2 3 4), jne.; ((1±i)/, jne.)
- 3 kpl: 180°:n rotaatiot samojen akselien ympäri: 3 akselia, 1 rotaatio aksellia kohti, yhteensä 3 ((1 2) (3 4), jne.; i,j,k)
- 6 kpl: 180°:n rotaatiot kunkin särmän keskipisteestä kuution keskipisteen kautta vastakkaisen särmän keskpisteeseen kulkevan akselin ympäri: 6 akselia, yksi rotaatio akselia kohti, ((1 2), jne.; ((i±j)/, jne.)
- 8 kpl: 120°:n rotaatiot kuution avaruuslävistäjien ympäri: 4 akselia, 2 rotaatiota kutakin akselia kohti, ((1 2 3), jne.; (1±i±j±k)/2)
Kaikki edellä mainitut (yhteensä 24 kpl) voidaan konkreettisesti toteuttaa kääntämällä kuutio toiseen asentoon. Lisäksi kuutiolla on vielä toiset 24 inversiota, jotka saadaan yhdistämällä jokin edellisistä inversion eli kuution keskipisteen suhteen suoritettavan peilauksen kanssa (jossa piste x kuvautuu pisteeseen −x; toiset 24 isometriaa). On huomattava, että 180°:n rotaatio akselin ympäri yhdistettynä inversion kanssa johtaa samaan tulokseen kuin peilaus tätä akselia vastaan kohtisuoran tason suhteen. Inversion sekä avaruuslävistäjän ympäri suoritetun 120°:n rotaation yhdistetty kuvaus taas on sama kuin sama kuin avaruuslävistäjän ympäri suoritettu 60°:n rotaatio yhdistettynä kohtisuoran tason suhteen suoritetun peilauksen kanssa. Tällainen rotaatio sinänsä ei kuvaa kuutiota itselleen, vaan peilaustason ja kuution leikkauspintana saadaan säännöllinen kuusikulmio.
Kuution isometriat voidaan yksilöidä useilla eri tavoilla:
- niiden tahkojen mukaan, joille kolme annettua tahkoa (esimerkiksi ne tahkot, joilla nopassa on luvut 1, 2 ja 3) kuvautuvat;
- kuvan mukaan, joka kuutiosta saadaan, kun sen johonkin tahkoon on tehty epäsymmetrinen merkintä: kunkin isometrian osoittaa se tahko, johon tämä kuva isometriassa siirtyy, sekä sen orientaatio ynnä se seikka, onko se muuttunut peilikuvakseen vai ei;
- neljän avaruuslävistäjän permutaatioiden mukaan (kaikki 24 permutaatiota ovat mahdollisia), varustettuna lisämerkillä, joka osoittaa, onko inversio tapahtunut vai ei.
Jos kuution tahkot on väritetty eri värein tai jos sen tahkoille on tehty erilaisia merkintöjä, kuten nopassa, kuution symmetriaryhmä on jokin Oh:n aliryhmä.
Esimerkiksi:
- C4v, [4], (*422): jos yhdellä tahkoista on muista poikkeava väri (tai jos kahdella vastakkaisella tahkolla on kummallakin oma värinsä, joka on eri kuin neljällä muulla), kuutiolla on 8 isometriaa samoin kuin neliöllä kahdessa ulottuvuudessa.
- D2h, [2,2], (*222): jos vastakkaisilla tahkoilla on sama väri mutta kullakin kolmesta kahden vastakkaisen tahkon parilla on eri värit, kuutiolla on 8 isometriaa samoin kuin kuboidilla.
- D4h, [4,2], (*422): jos kahdella vastakkaisella tahkolla on sama väri ja kaikilla muilla tahkoilla jokin toinen väri, kuutiolla on 16 isometriaa, samoin kuin neliöpohjaisella särmiöllä.
- C2v, [2], (*22):
- jos kahdella viereisellä tahkolla on sama väri ja kaikilla muilla jokin toinen väri, kuutiolla on 4 isometriaa.
- jos kolmella tahkolla, joista kaksi on vastakkaisia, on yksi väri ja muilla kolmella tahkolla toinen väri, kuutiolla on 4 isometriaa.
- jos kahdella vastakkaisella tahkolla on sama väri, kahdella muulla vastakkaisella tahkolla toinen yhteinen väri ja lopuilla kahdella kummallakin eri väri, kuutiolla on 4 symmetriaa, samoin kuin peilisymmetrisellä tyhjällä paperiarkilla.
- Cs, [ ], (*):
- jos kahdella vierekkäisellä sivulla on kummallakin eri väri ja neljällä muulla jokin muu väri, mutta nämä ovat kaikki samanvärisiä, kuutiolla on 2 iseometriaa.
- jos kahdella vastakkaisella sivulla on sama väri ja muilla sivuilla kullakin eri värit, kuutiolla on 2 isometriaa, samoin kuin epäsymmetrisellä paperipalalla.
- C3v, [3], (*33): jos kolmella tahkolla, joista yksikään ei toiselle vastakkainen, on sama väri ja kolmella muulla toinen yhteinen väri, kuutiolla on 6 isometriaa.
Kuution symmetriaryhmällä on suurempiakin aliryhmiä, mutta pelkästään värittämällä kuution tahkot eri väreillä ei voida saada kappaleita, joiden symmetriaryhmiä ne ovat. Sen sijaan piirtämällä tahkoille erilaisia kuvioita voidaan saada kappaleita, joiden symmetriaryhmiä nekin ovat.
Esimerkiksi:
- D2d, [2+,4], (2*2): jos yhdelle tahkolle on piirretty jana, joka jakaa tahkon kahteen yhtä suureen suorakulmioon, ja vastakkaisella tahkolla on vastaava jana kohtisuorassa suunnassa, näin saadulla kuutiolla on 8 isometriaa. Sillä on symmetriataso ja kaksinkertainen rotaatiosymmetria akselin ympäri, joka on 45°:n kulmassa tähän tasoon nähden, sekä tämän seurauksena toinenkin symmetriataso, joka on edelliseen nähden kohtisuorassa samoin kuin toinenkin akseli, jonka suhteen sillä on kaksinkertainen rotaatiosymmetria.
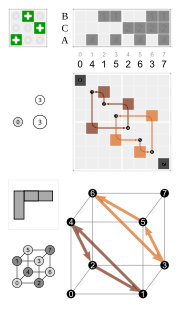
- Th, [3+,4], (3*2): Jos jokaiselle tahkolle on piirretty jana, joka jakaa sen kahteen yhtä suureen suorakulmioon siten, että vierekkäisille sivuille piirretyt janat eivät kohtaa toisiaan särmillä, kuutiolla on 24 isometriaa: kappaleen avaruuslävistäjien parilliset permutaatiot sekä ne yhdistettynä inversion kanssa (jossa x kuvautuu pisteeseen −x).
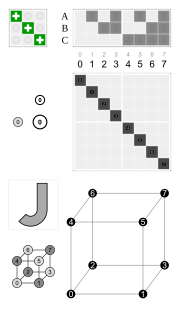
- Td, [3,3], (*332): Jos kuutio koostuu kahdeksasta pienemmästä kuutioista, joista neljä on valkoisia ja neljä mustia ja ne on sijoitettu niin, ettei kaksi samanväristä kuutiota kosketa toisiaan muutoin kuin kulmittain särmillä, kuutiolla on 24 isometriaa: kuution avaruuslävistäjien permutaatiot sekä muiden rotaatioiden inversiot.
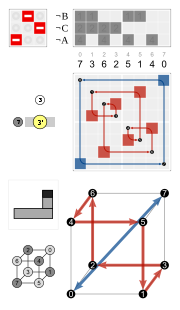
- T, [3,3]+, (332): jos jokaisella tahkolla on sama kuvio, jolla on kaksinkertainen rotaatiosymmetria, esimerkiksi S-kirjain, siten että jokaisella särmällä S:n huippu kohtaa toisella tahkolla olevan S:n sivun, kuutiolla on 12 isometriaa: avaruuslävistäjien permutaatiot ja vain ne.
Kuution täysi symmetria, Oh, [4,3], (*432), säilyy, jos ja vain jos kaikilla tahkoilla on sama kuvio siten, että niillä on täysi neliön symmetria, toisin sanoen diedrinen symmetria Dih4, [4], kertalukua 8.
Kuution täysi aitojen rotaatioiden muodostama symmetria, O, [4,3]+, (432), säilyy vain, jos kaikilla tahkoilla on sama kuvio, jolla on nelinkertainen rotaatiosymmetria C4, [4]+.
Bolzan pinnan oktaedrinen symmetria
[muokkaa | muokkaa wikitekstiä]- Riemannin pintojen teoriassa Bolzan pinta, jota joskus sanotaan myös Bolzan käyräksi, saadaan peittämällä Riemannin pinta kahteen kertaan niin, että se haarautuu pallon sisään piirretyn säännöllisen oktaedrin kärkipisteissä. Sen automorfismien ryhmään kuuluu hyperelliptinen involuutio, joka vaihtaa peitteen kaksi lehteä keskenään. Symmetriaryhmän tekijäryhmä hyperelliptisen involuution virittämän, kertalukua 2 olevan aliryhmän suhteen on täysin oktaedrin symmetriaryhmän kaltainen. Bolzan pinnan moniin huomattaviin ominaisuuksiin kuuluu, että sillä on kaikista genuksen 2 hyperbolisista pinnoista suurin systoli.
Kappaleet, joilla on kiraalinen oktaedrinen symmetria
[muokkaa | muokkaa wikitekstiä]| Luokka | Nimi | Kuva | Tahkoja | Särmiä | Kärkiä | Duaalikappaleen nimi | Kuva |
|---|---|---|---|---|---|---|---|
| Arkhimedeen kappale Catalanin kappale |
pullistettu kuutio |  |
38 | 60 | 24 | viisikulmainen ikositetraedri | 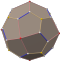
|
Kappaleet, joilla on täysi oktaedrinen symmetria
[muokkaa | muokkaa wikitekstiä]| Luokka | Nimi | Kuva | Tahkoja | Särmiä | Kärkiä | Duaalikappaleen nimi | Kuva |
|---|---|---|---|---|---|---|---|
| Platonin kappale | Kuutio |  |
6 | 12 | 8 | Oktaedri | 
|
| Arkhimedeen kappale (duaali Catalanin kappale) |
Kuboktaedri |  |
14 | 24 | 12 | Rombidodekaedri | 
|
| Typistetty kuutio |  |
14 | 36 | 24 | Triakis-oktaedri | 
| |
| Typistetty oktaedri |  |
14 | 36 | 24 | Tetrakis-heksaedri | 
| |
| Rombikuboktaedri |  |
26 | 48 | 24 | Deltoidaalinen ikositetraedri | 
| |
| Typistetty kuboktaedri |  |
26 | 72 | 48 | Disdyakis-dodekaedri | 
| |
| Säännöllinen komponentti- monitahokas |
Stella octangula |  |
8 | 12 | 8 | Itseduaalinen | |
| Kuution ja oktaedrin yhdistelmä | 
|
14 | 24 | 14 | Itseduaalinen |
Lähteet
[muokkaa | muokkaa wikitekstiä]- Peter R. Cromwell: Polyhedra, s. 295. {{{Julkaisija}}}.
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass: The Symmetry of Things. {{{Julkaisija}}}, 2008. ISBN 978-1-56881-220-5.
- F. Arthur Sherk, Peter McMullen, Anthony C. THompson, Asia Ivic Weiss (toim.): Kaleidoscopes: Selected Writings of H.S.M. Cozeter. Wiley-Interscience Publication, 1995. ISBN isbn. Teoksen verkkoversio.
- N. W. Johnson: ”Chapter 11.5: Finite symmetry groups, Spherical Coxeter groups”, Geometries and Transformations. {{{Julkaisija}}}, 2018. ISBN 978-1-107-10340-5.
Viitteet
[muokkaa | muokkaa wikitekstiä]- ↑ John Conway, The Symmetries of Things, Fig 20.8, p280
Katso myös
[muokkaa | muokkaa wikitekstiä]Aiheesta muualla
[muokkaa | muokkaa wikitekstiä]- Octahedral Group Wolfram MathWorld. Erik W. Weisstein. Viitattu 29.7.2019.

























































![{\displaystyle \left[{\begin{smallmatrix}1&0&0\\0&1&0\\0&0&-1\\\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af5dcd32706ab62613231faa8c808e8dc141f4b1)
![{\displaystyle \left[{\begin{smallmatrix}1&0&0\\0&0&1\\0&1&0\\\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/360ffd98d569298196c39d9d2daba3cd34ce0b0e)
![{\displaystyle \left[{\begin{smallmatrix}0&1&0\\1&0&0\\0&0&1\\\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e0e6c5ed4b85a87319dfaea9b7156ef7c6d2842)
![{\displaystyle \left[{\begin{smallmatrix}1&0&0\\0&0&1\\0&-1&0\\\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c6cb2345e2754c085c7c8a3134d3afee080d3eb8)
![{\displaystyle \left[{\begin{smallmatrix}0&1&0\\0&0&1\\1&0&0\\\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8f0760c23277fb7d553bb7fcd92d5ab21ca9003f)
![{\displaystyle \left[{\begin{smallmatrix}0&1&0\\1&0&0\\0&0&-1\\\end{smallmatrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a897b891b51ee772090abd9411192b580ac981b)