Geometrinen jakauma

Geometric

Todennäköisyysfunktio
Kertymäfunktio
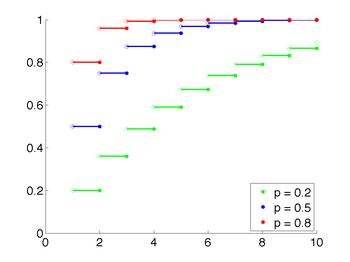
Parametrit	$0<p\leq 1$ onnistumisen todennäköisyys (reaaliluku)
Määrittelyjoukko	k epäonnistumista, missä $k\in \{0,1,2,3,\dots \}\!$
Pistetodennäköisyysfunktio	$(1-p)^{k}\,p\!$
Kertymäfunktio	$1-(1-p)^{k+1}\!$
Odotusarvo	${\frac {1-p}{p}}\!$
Mediaani	$\left\lceil {\frac {-1}{\log _{2}(1-p)}}\right\rceil \!-1$ (ei yksikäsitteinen, jos $-1/\log _{2}(1-p)$ on kokonaisluku)
Moodi	$0$
Varianssi	${\frac {1-p}{p^{2}}}\!$
Vinous	${\frac {2-p}{\sqrt {1-p}}}\!$
Huipukkuus	$6+{\frac {p^{2}}{1-p}}\!$
Entropia	${\tfrac {-(1-p)\log _{2}(1-p)-p\log _{2}p}{p}}\!$
Momentit generoiva funktio	${\frac {p}{1-(1-p)e^{t}}}\!$
Karakteristinen funktio	${\frac {p}{1-(1-p)\,e^{it}}}\!$

Geometrinen jakauma on dikotomisen toistokokeen ensimmäisen tulosta edeltävien kokeiden lukumäärän jakauma.

Geometrinen jakauma on diskreetti, ja sen arvojoukko on luonnollisten lukujen joukko. Jos satunnaismuuttuja $X$ on geometrisesti jakautunut, merkitään

$X\sim \operatorname {Geom} (p).$

Jakauman parametri $0\leq p\leq 1$ on tuloksen todennäköisyys. Pistetodennäköisyysfunktio on

$\operatorname {P} (X=i)=p(1-p)^{i}$

ja kertymäfunktio

$\operatorname {P} (X\leq i)=1-(1-p)^{i+1}$

Odotusarvo ja varianssi ovat

$\operatorname {E} (X)={\frac {1-p}{p}}$ ja $\operatorname {Var} (X)={\frac {1-p}{p^{2}}}.$

Aiheesta muualla

• Mathworld: Geometric Distribution
• Online laskin Geometrinen jakauma

Todennäköisyysjakaumat