Eksponenttijakauma

Eksponenttijakauma

Tiheysfunktio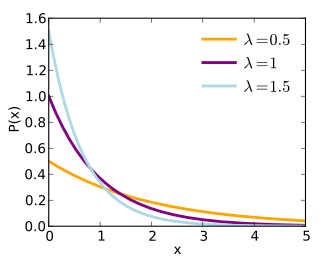
Kertymäfunktio
Parametrit	λ > 0 rate, or inverse skaala
Määrittelyjoukko	x ∈ [0, ∞)
Tiheysfunktio	λ e−λx
Kertymäfunktio	1 − e−λx
Odotusarvo	λ−1
Mediaani	λ−1 ln 2
Moodi	0
Varianssi	λ−2
Vinous	2
Huipukkuus	6
Entropia	1 − ln(λ)
Momentit generoiva funktio	$\left(1-{\frac {t}{\lambda }}\right)^{-1}\,$
Karakteristinen funktio	$\left(1-{\frac {it}{\lambda }}\right)^{-1}\,$

Eksponenttijakauma on muistinmenetysominaisuuden omaava ja Poisson-prosessin insidenssien välisen ajan jakauma.

Eksponenttijakauma on jatkuva, ja sen arvojoukko on positiivisten reaalilukujen joukko. Jos satunnaismuuttuja $X$ on eksponenttijakautunut, merkitään

$X\sim \operatorname {Exp} (\lambda ).$

Parametri $\lambda >0$ on jakauman odotusarvon käänteisluku. Tiheysfunktio on arvojoukossa

$f_{X}(x)=\lambda e^{-\lambda x}$

ja kertymäfunktio

$F_{X}(x)=1-e^{-\lambda x}.$

Odotusarvo ja varianssi ovat

$\operatorname {E} (X)={\frac {1}{\lambda }}$ ja $\operatorname {Var} (X)={\frac {1}{\lambda ^{2}}}.$

Eksponenttijakaumalla on niin kutsuttu muistinmenetysominaisuus, eli jos $a>0$, niin

$\operatorname {P} (X>x+a\,|\,X>a)=\operatorname {P} (X>x).$

Siis jos $X$ on esimerkiksi elinaika, niin muistinmenetysominaisuuden mukaan jäljellä oleva elinaika ei riipu iästä. Jatkuvista jakaumista vain eksponenttijakaumalla on muistinmenetysominaisuus.

Katso myös

• Gamma-jakauma

Aiheesta muualla

• Mathworld: Exponential Distribution
• Online laskin Eksponenttijakauma

Todennäköisyysjakaumat

Diskreettejä jakaumia	Bernoullin jakauma Binomijakauma Geometrinen jakauma Hypergeometrinen jakauma Negatiivinen binomijakauma Poissonin jakauma
Jatkuvia jakaumia	Beta-jakauma Cauchy-jakauma Eksponenttijakauma F-jakauma Gamma-jakauma Khii toiseen -jakauma Log-normaalijakauma Normaalijakauma Pareto-jakauma Studentin t-jakauma Tasajakauma Weibull-jakauma
Moniulotteisia jakaumia	Dirichlet-jakauma Moniulotteinen Studentin t-jakauma Multinomijakauma Multinormaalijakauma