Algebrallinen funktio

Algebrallinen funktio on matematiikassa sellainen funktio $y=f(x)$, joka voidaan määritellä yhtälöllä, jossa jokin muuttujista x ja y riippuva polynomi on asetettu nollaksi.. Toisin sanoen funktio voidaan esittää jonkin x:stä ja y:stä riippuvan polynomiyhtälön p(x,y) = 0 ratkaisuna.

Monet algebralliset funktiot voidaan esittää algebrallisena lausekkeina, jotka voidaan muodostaa muuttujasta ja äärellisestä määrästä vakioita pelkästään algebrallisten operaatioiden, toisin sanoen yhteen-, vähennys-, kerto- ja jakolaskun sekä juurenoton avulla. Sellaisia funktioita ovat esimerkiksi:

• $f(x)=1/x$
• $f(x)={\sqrt {x}}$
• $f(x)={\frac {\sqrt {1+x^{3}}}{x^{3/7}-{\sqrt {7}}x^{1/3}}}$

Abelin–Ruffinin lause osoittaa kuitenkin, että on olemassa myös algebrallisia funktioita, joita ei voida tällä tavoin muodostaa. Sellainen on esimerkiksi Bringin radikaali, joka on lausekkeen

$f(x)^{5}+f(x)+x=0$.

määrittelemä implisiittifunktio.

Täsmällisemmin ilmaistuna yhden muuttujan (x') n:nnen asteen algebrallinen funktio on funktio $y=f(x),$ joka on jatkuva määrittelyjoukossaan ja joka toteuttaa polynomiyhtälön

$a_{n}(x)y^{n}+a_{n-1}(x)y^{n-1}+\cdots +a_{0}(x)=0$

missä kertoimet $a_{i}(s)$ ovat x:n polynomifunktioita, joissa kertoimet ovat kokonaislukuja. Voidaan osoittaa, että sama funktioluokka saadaan, jos kertoimiksi $a_{i}$ hyväksytään mitkä tahansa algebralliset luvut. Jos kertoimina esiintyy transkendenttilukuja, funktio ei yleensä ole algebrallinen, mutta sen sanotaan olevan algebrallinen näiden kertoimien virittämän kunnan suhde.

Kun algebrallisen funktion argumentti on rationaaliluku tai mikä tahansa algebrallinen luku, funktion arvo on aina algebrallinen luku. Toisinaan tarkastellaan kertoimia $a_{i}<(x)$, jotka ovat jonkin renkaan R polynomeja, ja niitä sanotaan R:n algebrallisiksi funktioiksi.

Funktioita, jotka eivät ole algebrallisia, sanotaan transkendenttifunktioiksi. Sellaisia ovat esimerkiksi eksponenttifunktio $e^{x}$, trigonometriset funktiot kuten $\sin x$ ja $\cos x$, logaritmifunktio $\ln x$ ja gammafunktio $\Gamma (x)$. Transkendenttistenkin funktioiden yhdistetty funktio saattaa olla algebrallinen: esimerkiksi $f(x)=\cos \arcsin x={\sqrt {1-x^{2}}}$.

Koska n:nnen asteen polynomiyhtälöllä on enintään n ratkaisua (ja tasan n ratkaisua, jos kyseessä on algebrallisesti suljettu kunta, esimerkiksi kompleksilukujen kunta), polynomiyhtälö ei implisiittisesti määrittele vain yhtä funktiota, vaan enintään n funktiota, joita toisinaan sanotaan funktion haaroiksi. Tarkastellaan esimerkkinä yksikköympyrää:

$y^{2}+x^{2}=1.\,$

Tässä kutakin välillä -1 < x < 1 olevaa x:n arvoa kohti on kaksi y:n arvoa, jotka ovat toistensa vastalukuja. Niinpä yhtälö määrittelee kaksi haaraa:

$y=\pm {\sqrt {1-x^{2}}}.\,$

Vastaavasti m muuttujan algebrallinen funktio määritellään funktiona

$y=f(x_{1},\dots ,x_{m})$

joka on m + 1 muuttujan polynomiyhtälön

$p(y,x_{1},x_{2},\dots ,x_{m})=0.$

ratkaisu.

Yleensä edellytetään, että p:n on oltava jaoton polynomi. Siinä tapauksessa algebrallisen funktion olemassaolon takaa implisiittifunktiolause.

Muodollisesti m muuttujan algebrallinen funktio kunnassa K on rationaalilukujen kunnan algebrallisen sulkeuman K(x₁, ..., x_m) alkio.

Yhden muuttujan algebralliset funktiot

Johdanto ja yleiskatsaus

Algebrallisten yhtälöiden epämuodollinen määritelmä tarjoaa vihjeitä sellaisten ominaisuuksista. Intuitiivisen ymmärryksen saamiseksi voidaan algebralliset funktiot käsittää funktioiksi, jotka voidaan muodostaa tavanomaisilla algebrallisilla toimituksilla: yhteen-, kerto- ja jakolaskuilla sekä juurenotoilla. Tämä on kuitenkin yksinkertaisuus, sillä Galois’n teorian peruslauseesta seuraa, ettei kaikkia algebrallisia funktioita voida esittää juurilausekkeina.

Ensinnäkin voidaan todeta, että jokainen polynomifunktio $y=p(x)$ on algebrallinen funktio, sillä se on yksinkertaisesti yhtälön

$y-p(x)=0.\,$

ratkaisu y.

Myös jokainen rationaalifunktio$y={\frac {p(x)}{q(x)}}$ on yhtälön

$q(x)y-p(x)=0.$

ratkaisuna algebrallinen.

Jokaisen polynomin n:s juuri eli muotoa ${\textstyle y={\sqrt[{n}]{p(x)}}}$ oleva funktio on myös algebrallinen, sllä se on yhtälön

$y^{n}-p(x)=0.$

ratkaisu.

Hieman yllättävämpää on, että jokaisen algebrallisen funktion käänteisfunktio on myös algebrallinen. Sillä jos oletetaan, että y on yhtälön

$a_{n}(x)y^{n}+\cdots +a_{0}(x)=0,$

ratkaisu jokaisella x:n arvolla, on x myös tämän yhtälön ratkaisu jokaisella y:n arvolla. Itse asiassa vaihtamalla x:n ja y:n merkitykset keskenään ja yhdistämällä termejä saadaan

$b_{m}(y)x^{m}+b_{m-1}(y)x^{m-1}+\cdots +b_{0}(y)=0.$

Nyt kirjoittamalla x y:n funktiona saadaan alkuperäisen funktion käänteisfunktio, joka on myös algebrallinen funktio.

Kaikilla funktioilla ei kuitenkaan ole käänteisfunktiota. Esimerkiksi funktio y = x² ei ole bijektio, vaan se saa argumentin arvoilla x ja -x aina saman arvon. Jos tästä yhtälöstä ratkaistaan x, saadaan kaksiarvoinen lauseke $x=\pm {\sqrt {y}}$. Sen molemmat haarat, ${\sqrt {y}}$ ja $-{\sqrt {y}}$ ovat kuitenkin algebrallisia funktioita, mutta reaalilukujen joukossa $\mathbb {R}$ ne on määritelty vain, kun $y\geq 0$.

Kompleksilukujen merkitys

Algebran näkökulmasta kompleksiluvut liittyvät täysin luonnollisella tavalla algebrallisten funktioiden teoriaan. Ensinnäkin algebran peruslauseen mukaan kompleksiluvut ovat algebrallisesti suljettu kunta. Siitä seuraa, että jos y:n sallitaan olla myös kompleksiluku, niin polynomirelaatiolla p(y, x) = 0 on varmasti vähintään yksi ratkaisu jokaisessa pisteessä x, ja yleensä niin monta ratkaisua kuin p:n asteluku y:n suhteen osoittaa. Tämän vuoksi algebrallisten funktioiden määrittelyalueesta johtuvat ongelmat minimoituvat.

Algebrallisen funktion y kolmen haaran kuvaajat, missä y³ − xy + 1 = 0, alueella 3/2^2/3 < x < 50.

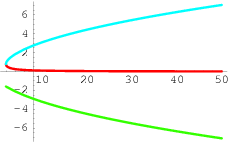
Lisäksi siinäkin tapauksessa, että ollaan kiinnostuneita vain reaalisista algebrallisista funktioista, eräissä tapauksissa ei ole keinoa esittää funktiota yhteen-, kerto- ja jakolaskun sekä juurenoton avulla ilman, että joudutaan tekemisiin myös kompleksilukujen kanssa. Tarkastellaan esimerkiksi algebrallista funktiota, jonka määrittelee yhtälö

$y^{3}-xy+1=0.\,$

Kolmannen asteen yhtälön ratkaisukaavan avulla saadaan

$y=-{\frac {2x}{\sqrt[{3}]{-108+12{\sqrt {81-12x^{3}}}}}}+{\frac {\sqrt[{3}]{-108+12{\sqrt {81-12x^{3}}}}}{6}}.$

Kun $x\leq {\frac {3}{\sqrt[{3}]{4}}},$, kaavassa esiintyvä neliöjuuri on reaalinen ja kuutiojuurikin näin ollen hyvin määritelty ja saadaan vain yksi reaalinen ratkaisu. Sitä vastoin alueella $x>{\frac {3}{\sqrt[{3}]{4}}},$ tämä neliöjuuri ei ole reaalinen, ja niinpä sen arvoksi on valittava jompikumpi kahdesta imaginaariluvusta, jotka ovat toistensa vastalukuja. Niinpä kuutiojuuri on valittava kolmen ei-reaalisen luvun joukosta. Jos sama valinta tehdään kaavan kummassakin termissä, nämä kolme kuutiojuuren valintaa antavat tulokseksi oheisessa kuvassa esiintyvät kolme haaraa.

Voidaan todistaa, ettei tätä funktiota voida mitenkään esittää lausekkeella, jossa esiintyy vain reaalilukujen juuria, vaikka nämä funktiot ovatkin reaalisia tässä kaaviossa näkyvällä alueella.

Merkittävämmällä teoreettisella tasolla kompleksilukujen käyttö antaa mahdollisuuden käyttää kompleksianalyysin vahvoja tekniikoita algebrallisten funktioiden tutkimiseen. Erityisesti argumenttiperiaatteen avulla voidaan osoittaa, että jokainen algebrallinen funktio on samalla analyyttinen funktio ainakin moniarvoisen funktion merkityksessä.

Olkoon p(x, y) kompleksimuuttujien x ja y kompleksiarvoinen funktio. Oletetaan, että x₀ ∈ C on sellainen, että y:n polynomilla p(x₀, y) on n erillistä nollakohtaa. Osoitamme, että algebrallinen funktio on analyyttinen jossakin x₀ ympäristössä. Vallitaan joukko n toisiaan leikkaamatonta kiekkoa Δ_i, joista jokainen sisältää yhden näistä nollakohdista. Silloin argumenttiperiaatteen mukaan

${\frac {1}{2\pi i}}\oint _{\partial \Delta _{i}}{\frac {p_{y}(x_{0},y)}{p(x_{0},y)}}\,dy=1.$

Jatkuvuuden nojalla tämä pätee myös kaikille arvoille x jossakin x₀:n ympäristössä. Erityisesti p(x, y):llä on vain yksi nollakohta kiekossa Δ_i, mikä seuraa residylauseesta:

$f_{i}(x)={\frac {1}{2\pi i}}\oint _{\partial \Delta _{i}}y{\frac {p_{y}(x,y)}{p(x,y)}}\,dy$

mikä on analyyttinen funktio.

Monodromia

Edellä esitetyssä analyyttisyyden todistuksessa johdettiin lauseke n erillisen funktioelementin f_i(x) järjestelmälle, edellyttäen, että x ei ole p(x, y):n kriittinen piste. Kriittinen piste on piste, jossa erillisten nollakohtien lukumäärä on pienempi kuin p:n aste, ja näin tapahtuu vain siellä, missä p:n korkea-asteisin termi ja diskriminantti saavat arvon nolla. Näin sellaisia pisteitä c₁, ..., c_m on vain äärellinen määrä.

Funktioelementtien f_i tarkempaa tutkimusta kriittisten pisteiden lähellä voidaan käyttää osoittamaan, että monodrominen peite haarautuu kriittisten pisteiden sekä mahdollisesti myös kompleksitason äärettömyyspisteen ympärillä. Niinpä f_i:n holomorfisella laajennuksella on vähintään algebralliset navat ja tavalline algebrallinen haarautuma kriittisten pisteiden ympärillä.

On huomattava, että kriittisten pisteiden ympärillä pätee /

$p(x,y)=a_{n}(x)(y-f_{1}(x))(y-f_{2}(x))\cdots (y-f_{n}(x))$,

sillä pisteet f_i ovat määritelmän mukaan p:n erilliset nollakohdat. Monodromiaryhmän muodostavat näiden tekijöiden permutaatiot, ja näin ollen ne muodostavat p:n Galois’n ryhmän monodromisen esityksen.

Historia

Algebrallisten funktioiden keskeisimmät ideat tunsi ainakin jo René Descartes. Ensimmäinen järjestelmällinen esitys niistä lienee Edward Waringin teoksessa An essay on the Principles of Human Knowledge, jossa hän kirjoitti:

"Olkoon ordinaattaa kuvaava suure abskissan x algebrallinen funktio, joka on muodostettu tavanomaisilla jakolaskuilla ja juurenotoilla. Kehitetään se nousevaksi tai laskevaksi päättymättömäksi sarjaksi x:n ulottuvuuksien mukaan ja muodostetaan sitten jokaisen saadun termin integraali."

Katso myös

• Analyyttinen funktio
• Alkeisfunktio
• Funktio
• Polynomi
• Rationaalifunktio
• Erikoisfunktio

Lähteet

• Lars Ahlfors: Complex Analysis. McGraw Hill, 1979.
• Bartel Leendert van der Waerden: Modern Algebra, Volume II. Springer, 1931.
• Algebraic function Planet Math. Viitattu 14.7.2022.