Pistetulo

Pistetulo eli skalaaritulo on matematiikassa vektoreille määritelty lasku­toimitus, jonka tulos on skalaari. Euklidisen avaruuden tapauksessa sitä nimitetään joskus myös sisätuloksi tai projektio­tuloksi, joka korostaa sen geometrista, vektorin projektioon liittyvää merkitystä. Vektorit voidaan ilmaista järjestetyillä luku­jonoilla, joista kummassakin on piste­tuloa muodostettaessa oltava yhtä monta lukua (ne ilmoittavat yleensä vektorin koordinaatit, kun taas vektorien piste­tulo on vain yksi luku.

Nimitys pistetulo johtuu siitä, että sen merkkinä yleensä käytetään vektorien symbolien väliin merkittyä pistettä samaan tapaan kuin pistettä lukujen välissäkin käytetään (vinoristin ohella) kertomerkkinä. Täten vektorien a ja b piste­tuloa merkitään a⋅b. Toisinaan kuitenkin käytetään myös merkintää (a,b). Pistetulon toinen nimi skalaari­tulo taas korostaa sitä, että tuloksena on skalaari. Kolmi­ulotteisessa avaruudessa vektoreille on pistetulon lisäksi määritelty toinenkin tulo, ristitulo, jonka tulos on pseudovektori ja jolle käytetään merkintää a × b. Ulottuvuuksien luku­määrästä riippumatta pistetulo liittyy suoraan vektorien välisen kulman kosiniin.

Määritelmä

Pistetulo voidaan määritellä kahdella tavalla: algebrallisesti tai geometrisesti. Geometrinen määritelmä perustuu kulman ja etäisyyden käsitteisiin, joista jälkimmäinen merkitsee myös vektorin suuruutta. Kun euklidisessa avaruudessa käytetään karteesista koordi­naatistoa, nämä määritelmät voidaan osoittaa yhtäpitäviksi.

Nykyaikaisessa analyyttisessä geometriassa avaruuden pisteet määritellään niiden karteesisten koordinaattien avulla, ja euklidinen avaruus itse samastetaan reaalisen koordinaatti­avaruuden $\mathbb {R} ^{n}$ kanssa. Tällaisessa lähestymistavassa pituuden ja kulman käsitteitä ei oleteta annettuina, vaan ne määritellään vasta pistetulon avulla: vektorin pituus määritellään neliöjuurena sen piste­tulosta itsensä kanssa, ja vektorien välinen kulma määritellään siten, että sen kosini on vektorien pistetulo jaettuna vektorien pituuksien tulolla. Tällöin piste­tulon algebrallisen ja geometrisen määritelmän yhtä­pitävyys on oleellinen osa euklidisen geometrian klassisen ja modernin, analyyttiseen geometriaan perustuvan muotoilun yhtä­pitävyyttä.

Algebrallinen määritelmä

Kahden vektorin A = [A₁, A₂, ..., A_n] ja B = [B₁, B₂, ..., B_n] pistetulo n-ulotteisessa avaruudessa määritellään seuraavasti:

$\mathbf {A} \cdot \mathbf {B} =\sum _{i=1}^{n}A_{i}B_{i}=A_{1}B_{1}+A_{2}B_{2}+\cdots +A_{n}B_{n}$

missä $\sum$ tarkoittaa summausta. Esimerkiksi kolmi­ulotteisessa avaruudessa vektorien [1, 3, -5] ja [4, -2, -1] pistetulo on:

${\begin{aligned}\ [1,3,-5]\cdot [4,-2,-1]&=1\cdot 4+3\cdot (-2)+(-5)\cdot (-1)\\&=4-6+5\\&=3.\end{aligned}}$

Geometrinen määritelmä

Euklidisessa avaruudessa vektori on geometrinen olio, jolla on sekä suuruus että suunta. Vektoria voidaan kuvata nuolella. Sen suuruus on nuolen pituus ja suunta se, mihin nuolen kärki osoittaa. Vektorin A pituudelle käytetään merkintää $\left\|\mathbf {A} \right\|$. Euklidisten vektorien A ja B piste­tulo määritellään seuraavasti:

$\mathbf {A} \cdot \mathbf {B} =\left\|\mathbf {A} \right\|\,\left\|\mathbf {B} \right\|\cos \theta ,$

missä $\theta$ on vektorien A ja B välinen kulma.

Erityisesti jos A ja B ovat kohtisuorassa, niiden välinen kulma on 90° ja

$\mathbf {A} \cdot \mathbf {B} =0.$

Toinen ääritapaus on, että vektorit ovat samansuuntaisia. Silloin niiden välinen kulma on 0° ja

$\mathbf {A} \cdot \mathbf {B} =\left\|\mathbf {A} \right\|\,\left\|\mathbf {B} \right\|$

Tästä seuraa, että vektorin A pistetulo itsensä kanssa on

$\mathbf {A} \cdot \mathbf {A} =\left\|\mathbf {A} \right\|^{2},$

mistä saadaan vektorin pituudelle lauseke

$\left\|\mathbf {A} \right\|={\sqrt {\mathbf {A} \cdot \mathbf {A} }}.$

Skalaaritulon perusominaisuuksia

Skalaariprojektio

Euklidisen vektorin A skalaariprojektio eli skalaarinen komponentti toisen euklidisen vektorin B suunnassa on määritelmän mukaan

$A_{B}=\left\|\mathbf {A} \right\|\cos \theta ,$

missä $\theta$ on vektorien A ja B välinen kulma.

Pistetulon geometriseen määritelmään perustuen tämä voidaan kirjoittaa myös muotoon

$A_{B}=\mathbf {A} \cdot {\widehat {\mathbf {B} }},$

missä ${\widehat {\mathbf {B} }}=\mathbf {B} /\left\|\mathbf {B} \right\|$ on B:n suuntainen yksikkövektori.

Pistetulon vaihdantalaki

Pistetuloa luonnehtii näin ollen geometrisesti

$\mathbf {A} \cdot \mathbf {B} =A_{B}\left\|\mathbf {B} \right\|=B_{A}\left\|\mathbf {A} \right\|.$

Tähän tapaan määriteltynä pistetulo on homogeeninen skaalattaessa jokaista muuttujaa, mikä merkitsee, että jokaiselle skalaarille $\alpha$ pätee:

$(\alpha \mathbf {A} )\cdot \mathbf {B} =\alpha (\mathbf {A} \cdot \mathbf {B} )=\mathbf {A} \cdot (\alpha \mathbf {B} ).$

Pistetulolle pätee myös osittelulaki, toisin sanoen

$\mathbf {A} \cdot (\mathbf {B} +\mathbf {C} )=\mathbf {A} \cdot \mathbf {B} +\mathbf {A} \cdot \mathbf {C} .$

Näistä ominaisuuksista yhteen­vetona voidaan todeta, että pistetulo on bilineaarinen muoto. Lisäksi tämä bilineaarinen muoto on positiivinen definiittinen, mikä merkitsee, että $\mathbf {A} \cdot \mathbf {A}$ ei ole koskaan negatiivinen, ja nolla se on jos ja vain jos $\mathbf {A} =\mathbf {0} .$

Määritelmien yhtäpitävyys

Jos e₁, ..., e_n ovat $\mathbb {r} ^{n}$:n standardikanta eli koordinaattiakselien suuntaiset yksikkövektorit, voidaan kirjoittaa:

${\begin{aligned}\mathbf {A} &=[A_{1},\dots ,A_{n}]=\sum _{i}A_{i}\mathbf {e} _{i}\\\mathbf {B} &=[B_{1},\dots ,B_{n}]=\sum _{i}B_{i}\mathbf {e} _{i}.\end{aligned}}$

Vektorit e_i muodostavat avaruuden ortonormaalin kannan, sillä ne kaikki ovat yhden pituusyksikön pituisia ja keskenään kohtisuorassa. Koska ne ovat yksikön pituisia, on

$\mathbf {e} _{i}\cdot \mathbf {e} _{i}=1$

ja koska ne ovat keskenään kohtisuorassa, jos $i\neq j$, on

$\mathbf {e} _{i}\cdot \mathbf {e} _{j}=0.$

Tällöin voidaan todeta, että kaikissa tapauksissa pätee:

$\mathbf {e} _{i}\cdot \mathbf {e} _{j}=\delta _{ij}.$

missä $\delta _{i}j$ on Kroneckerin delta.

Geometrisen määritelmän perusteella voidaan toisaalta todeta, että jokaiselle kanta­vektorille e_i ja jokaiselle vektorille A pätee:

$\mathbf {A} \cdot \mathbf {e} _{i}=\left\|\mathbf {A} \right\|\,\left\|\mathbf {e} _{i}\right\|\cos \theta =\left\|\mathbf {A} \right\|\cos \theta =A_{i},$

missä A_i on vektorin A komponentti yksikkö­vektorin e_i suunnassa.

Soveltamalla geometrisesti määritellyn pistetulon osittelulakia saadaan

$\mathbf {A} \cdot \mathbf {B} =\mathbf {A} \cdot \sum _{i}B_{i}\mathbf {e} _{i}=\sum _{i}B_{i}(\mathbf {A} \cdot \mathbf {e} _{i})=\sum _{i}B_{i}A_{i},$

mikä on täsmälleen sama kuin pistetulon algebrallinen määritelmä. Kahden vektorin geometrinen pistetulo on siis aina yhtä suuri kuin niiden algebrallinen pistetulo.

Laskusääntöjä

Jos a, b ja c ovat reaalikertoimisia vektoreita ja r skalaari, vektorien pistetulolla on seuraavat ominaisuudet.

1. Vaihdannaisuus:

   $\mathbf {a} \cdot \mathbf {b} =\mathbf {b} \cdot \mathbf {a} ,$

   seuraa suoraan määritelmästä ($\theta$ on vektorien a ja b välinen kulma).

   $\mathbf {a} \cdot \mathbf {b} =\left\|\mathbf {a} \right\|\left\|\mathbf {b} \right\|\cos \theta =\left\|\mathbf {b} \right\|\left\|\mathbf {a} \right\|\cos \theta =\mathbf {b} \cdot \mathbf {a} .$

2. Osittelulaki vektorien yhteenlaskun suhteen:

   $\mathbf {a} \cdot (\mathbf {b} +\mathbf {c} )=\mathbf {a} \cdot \mathbf {b} +\mathbf {a} \cdot \mathbf {c} .$

3. Bilineaarisuus:

   $\mathbf {a} \cdot (r\mathbf {b} +\mathbf {c} )=r(\mathbf {a} \cdot \mathbf {b} )+(\mathbf {a} \cdot \mathbf {c} ).$

4. Skalaarilla kertominen:

   $(c_{1}\mathbf {a} )\cdot (c_{2}\mathbf {b} )=c_{1}c_{2}(\mathbf {a} \cdot \mathbf {b} ).$

5. Ortogonaalisuus:

   Vektorit a ja b, jotka eivät ole nollavektoreita, ovat kohtisuorassa, jos ja vain jos a ⋅ b = 0.

6. Tulosääntö:

   Jos a ja b ovat funktioita, niiden tulon derivaatta, jonka merkkinä käytetään pilkkua ('), on a' ⋅ b + a ⋅ b'.

Sen sijaan piste­tulolle ei ole olemassa liitäntälakia. Tämä seuraa jo siitä, ettei skalaarin (a ⋅ b) ja vektorin (c) tai vektorin (a) ja skalaarin (b' ⋅ c) piste­tulo ole edes määritelty. Edellä mainittua skalaarilla kertomis­sääntöä sanotaan kuitenkin toisinaan "skalaarin ja pistetulon liitäntä­laiksi", tai sanotaan, että "pistetulo on liitännäinen skalaarilla kertomisen suhteen, koska c (a ⋅ b) = (c a) ⋅ b = a ⋅ (c b).

Myöskään supistussääntö ei päde. Tavallisille luvuillehan pätee, että jos ab = ac, on aina myös b = c, ellei a ole nolla. Näin ei kuitenkaan ole vektorien pistetulon laita, sillä jos a ⋅ b = a ⋅ c ja $a\neq 0$, tästä seuraa osittelu­lain mukaan, että a ⋅ (b - c) = 0: tämä edellyttää vain, että a on kohti­suorassa vektoria b − c vastaan, mutta vektorin b − c ei tarvitse olla nollavektori, joten b ei välttämättä ole yhtä suuri kuin c.

Kosinilauseen todistus pistetulon avulla

Kolmio, jonka kahtena sivuna ovat vektorit a ja b, joiden välinen kulma on $\theta$.

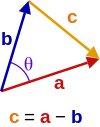
Oletetaan kaksi vektoria, a ja b, joiden välinen kulma $\theta$, kuten oheisessa kuvassa. Niiden avulla voidaan muodostaa kolmio, jonka kolmantena sivuna on vektori c = a - b. Tämän kolmannen sivun pistetulo itsensä kanssa on:

$\mathbf {c} \cdot \mathbf {c} =(\mathbf {a} -\mathbf {b} )\cdot (\mathbf {a} -\mathbf {b} )$

$=\mathbf {a} \cdot \mathbf {a} -\mathbf {a} \cdot \mathbf {b} -\mathbf {b} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b}$

$=a^{2}-\mathbf {a} \cdot \mathbf {b} -\mathbf {a} \cdot \mathbf {b} +b^{2}$

$=a^{2}-2\mathbf {a} \cdot \mathbf {b} +b^{2}$

Näin ollen on:

$c^{2}=a^{2}+b^{2}-2ab\cos \theta$,

mikä tulos tunnetaan kosinilauseena.

Lagrangen kaava

Vektorien piste- ja ristitulon yhdistää toisiinsa seuraava Lagrangen kaava:

$\mathbf {a} \times (\mathbf {b} \times \mathbf {c} )=\mathbf {b} (\mathbf {a} \cdot \mathbf {c} )-\mathbf {c} (\mathbf {a} \cdot \mathbf {b} ),$

mille voidaan käyttää muistisääntöä "BAC miinus CAB", kunhan muistetaan, mille vektoreille pistetulo muodostetaan. Tämän kaavan avulla vektoreilla suoritettavia lasku­toimituksia voidaan yksin­kertaistaa varsinkin fysiikassa.

Sovelluksia fysiikassa

Fysiikassa pistetulo on skalaari myös fysikaalisessa merkityksessä. Se on käytetystä koordinaatti­järjestelmästä riippumaton fysikaalinen suure, jolla on lukuarvo ja yksikkö. Esimerkkejä fysikaalisista suureista, joiden arvo voidaan laskea vektori­suureiden pistetulona, ovat muun muassa seuraavat:

• Voiman tekemä mekaaninen työ on kappaleeseen vaikuttavan voiman ja kappaleen kulkeman matkan pistetulo.
• Magneettivuo tietyn pinnan läpi on magneettivuon tiheyden ja pinta-alavektorin pistetulo, kun pinta-ala käsitetään vektoriksi, joka on kohti­suorassa pintaa vastaan.

Yleistyksiä

Kompleksivektorit

Sovellettuina vektoreihin, joiden komponentit ovat kompleksilukuja, edellä esitetyt pistetulon määritelmät antaisivat sille varsin erilaisia ominaisuuksia. Esimerkiksi vektorin pistetulo itsensä kanssa voisi olla mikä tahansa kompleksi­luku, ja se voisi myös olla nolla, vaikka kyseessä ei olisikaan nollavektori; sellaisia vektoreita sanotaan isotrooppisiksi; tällä taas olisi pituuden ja kulman käsitteisiin liittyviä seurauksia. On kuitenkin mahdollista määritellä kompleksi­vektoreillekin pistetulo siten, että se on ominaisuuksiltaan lähempänä reaali­vektoreiden pistetuloa ja että sillä esimerkiksi on aina positiivis-definiittinen normi. Tällöin pistetulo määritellään seuraavasti:

$\mathbf {a} \cdot \mathbf {b} =\sum {a_{i}{\overline {b_{i}}}},$

missä b_i on b_i:n kompleksikonjugaatti.

Näin määriteltynä jokaisen vektorin pistetulo itsensä kanssa on ei-negatiivinen reaaliluku, ja se on nolla vain, jos kyseessä on nollavektori. Näin määritellyllä kompleksi­vektorien piste­tulolla ei kuitenkaan ole reaali­vektorien pistetulon symmetria­ominaisuuksia eikä se ole bilineaarinen. Sen sijaan se on seskvilineaarinen: se on konjugaattilineaarinen, mutta ei lineaarinen b:n suhteen. Se ei myöskään symmetrinen, sillä

$\mathbf {a} \cdot \mathbf {b} ={\overline {\mathbf {b} \cdot \mathbf {a} }}.$

Kompleksivektorien välinen kulma määritellään tällöin seuraavasti:

$\cos \theta ={\frac {\operatorname {Re} (\mathbf {a} \cdot \mathbf {b} )}{\left\|\mathbf {a} \right\|\,\left\|\mathbf {b} \right\|}}.$

Tämäntyyppinen skalaaritulo on kaikesta huolimatta käyttö­kelpoinen, ja se johtaa hermiittisen muodon ja yleisen sisätulo­avaruuden käsitteisiin.

Sisätulo

Sisätulo on pistetulon yleistys abstarkteihin vektori­avaruuksiin, joiden kerroin­kuntana on joko reaalilukujen ($\mathbb {R}$) tai kompleksilukujen kunta ($\mathbb {C}$). Sisätulolle käytetään yleensä merkintää $\left\langle \mathbf {a} \,,\mathbf {b} \right\rangle$.

Kun kerroinkuntana ovat kompleksiluvut, kahden vektorin sisätulo on yleensä kompleksiluku, ja sisätulo on seskvilineaarinen, ei bilineaarinen. Sisätuloavaruus on normitettu vektoriavaruus, ja vektorin sisätulo itsensä kanssa on positiivis-definiittinen.

Funktioiden sisätulo

Sisätulo on määritelty vektoreille, joilla on äärellinen määrä komponentteja. Koska vektorit voidaan esittää lukujonoina^selvennä, voidaan n-vektori käsittää myös diskreetiksi funktioksi, joka on määritelty joukossa ${k\in N|1<=k<=n}$, jolloin u_i eli vektorin i:s komponentti on funktion arvo argumentin arvolla i.

Tämä käsite voidaan yleistää jatkuville funktiolle. Samoin kuin vektorien sisätulo lasketaan vastaavien komponenttien tulojen summana, funktion sisätulo määritellään integraalina jonkin välin a < x b yli, jolle välille käytetään myös merkintää [a,b]:

$\left\langle u,v\right\rangle =\int _{a}^{b}u(x)v(x)dx$

Tämä voidaan edelleen yleistää kompleksifunktioille $\psi (x)$ ja $\chi (x)$ samaan tapaan kuin kompleksivektorien sisätulo edellä määriteltiin. Tällöin saadaan:

$\left\langle \psi ,\chi \right\rangle =\int _{a}^{b}\psi (x){\overline {\chi (x)}}dx.$

Painofunktio

Sisätuloilla voi olla painofunktio, toisin sanoen funktio, joka painottaa sisätulon jokaista termiä jollakin arvolla.

Dyadit ja matriisit

Matriiseilla sisätuloa vastaa Frobeniuksen sisätulo, joka on analoginen vektorien sisätulon kanssa. Kahden matriisin Frobeniuksen sisätulo on määritelty edellyttäen, että kummassakin on yhtä monta riviä ja yhtä monta saraketta. Tällöin matriisien A ja B sisätulo on niiden vastaavien komponenttien tulojen summa:

$\mathbf {A} :\mathbf {B} =\sum _{i}\sum _{j}A_{ij}{\overline {B_{ij}}}=\mathrm {tr} (\mathbf {B} ^{\mathrm {H} }\mathbf {A} )=\mathrm {tr} (\mathbf {A} \mathbf {B} ^{\mathrm {H} }).$

$\mathbf {A} :\mathbf {B} =\sum _{i}\sum _{j}A_{ij}B_{ij}=\mathrm {tr} (\mathbf {B} ^{\mathrm {T} }\mathbf {A} )=\mathrm {tr} (\mathbf {A} \mathbf {B} ^{\mathrm {T} })=\mathrm {tr} (\mathbf {A} ^{\mathrm {T} }\mathbf {B} )=\mathrm {tr} (\mathbf {B} \mathbf {A} ^{\mathrm {T} }).$ (reaalikertoimisille matriiseille)

Samaan tapaan myös dyadeille on määritelty sisätulo ja "kaksinkertainen" sisätulo.

Tensorit

Kahden tensorin sisätulo, joista toinen on astetta n ja toinen astetta m, on asteen n + m − 2 tensori.

Katso myös

• Cauchyn–Schwarzin epäyhtälö
• Ristitulo

Kirjallisuutta

• Kivelä, Simo K.: Algebra ja geometria. Espoo: Otatieto, 1989. ISBN 951-672-103-6.
• Rikkonen, Harri: Matematiikan pitkä peruskurssi I: Vektorialgebra ja analyyttinen geometria. Helsinki: Otakustantamo, 1969. ISBN 951-671-067-0.
• Pitkäranta, Juhani: Calculus Fennicus – TKK:n 1. lukuvuoden laaja matematiikka (2000–2013) (pdf) Helsinki: Avoimet oppimateriaalit ry. ISBN 978-952-7010-12-9 ISBN 978-952-7010-6 (pdf).

Aiheesta muualla

• Dot product Wolfram MathWorld.
• Explanation of dot product including with complex vectors mathreference.com.
• Dot Product demonstrations.wolfram.com. 2007.