Riemannin integraali

Käyrän y=f(x), x-akselin sekä suorien x=a ja x=b väliin jäävä tasokuvio S, jonka pinta-ala yritetään määrittää

Riemann-summien jono tasaväliselle ositukselle. Yläkulman luku on nelikulmioiden pinta-alojen summa, joka suppenee kohti integraalin arvoa osituksen tihetessä.

Välin ositus voi olla epäsäännöllinen, kunhan jokaisen osavälin pituus lähestyy nollaa.

Riemannin integraali on määrätty integraali, joka määrittää funktion kuvaajan alle jäävän etumerkillisen pinta-alan. Riemannin integraali määritellään jakamalla integroimisväli osaväleihin, joiden sisällä integroitavaa funktiota approksimoidaan vakiolla, ja laskemalla saatavat pinta-alat yhteen. Kun jakoa tihennetään, arvioi saatava summa integraalia yhä paremmin. Riemannin integraali saadaan tämän prosessin raja-arvona. Jatkuvan funktion Riemannin integraali voidaan laskea derivoinnin käänteisoperaationa analyysin peruslauseen avulla.

On olemassa funktioita, jotka ovat hyvin epäjatkuvia ja joita ei voi visualisoida yksinkertaisesti käyränä. Tällaisille funktioille ei voi laskea Riemannin integraalia, mutta esimerkiksi matemaattisesti hienostuneempi Lebesguen integraali saattaa olla olemassa. Jos funktion Riemannin integraali on olemassa, se vastaa arvoltaan Lebesguen integraalia.

Riemannin integraali oli ensimmäinen funktiolle reaaliakselin välin yli täsmällisesti määritelty integraali. Se on nimetty kehittäjänsä Bernhard Riemannin mukaan, joka esitteli sen vuonna 1854 habilitaatiotutkielmassaan. Riemann käytti määrittelemäänsä integraalia tutkiessaan Fourier-sarjojen suppenemisominaisuuksia.

Määritelmä

Riemannin integraalin määrittelyn tavoitteena on löytää yksiselitteinen pinta-ala reaalilukujen tason kuviolle, jonka rajaavat koordinaatistossa suorat $x=a$, $x=b$ ja $y=0$, sekä käyrä $y=f(x)$, missä $f$ on funktio $[a,b]\rightarrow \mathbb {R}$. Tutkittavat pinta-alat ovat etumerkillisiä. Toisin sanoen, jos $f$ saa negatiivisia arvoja, ovat pinta-alat negatiivisia. Tason kuvaamiseen käytetään merkintää:

$S=\int _{a}^{b}f(x)\,dx$

Funktion $f$ halutaan sallia olevan mahdollisimman yleinen, toisin sanoen tässä ei rajoituta integroitaviin funktioihin, jotka ovat jossakin mielessä sopivan sileitä. Tämän vuoksi tässä esiteltävä määritelmä saattaa olla monimutkaisempi kuin joissakin oppikirjoissa.

Tämä määrittely tehdään jakamalla väli $[a,b]$ osaväleihin, joita sitten tihennetään äärettömästi. Jokaisella osavälillä suoran $y=0$ ja käyrän $y=f(x)$ väliin jäävää pinta-alaa approksimoidaan suorakulmioilla. Jaon tihentyessä suorakaiteiden pinta-alojen summan pitäisi supeta kohti kysyttyä pinta-alaa. Riemannin integraalissa suorakaiteen korkeudeksi valitaan funktion $f$ arvo osavälin mielivaltaisessa pisteessä, jolloin jokaista jakoa vastaavan kuvion pinta-ala on niin kutsuttu Riemannin summa. Tässä annetaan kuitenkin myös Darboux'n integraalin määritelmä, missä valitaan kaksi suorakaiteen korkeutta, jotka ovat funktion $f$ maksimi ja minimi kullakin osavälillä, ja sen jälkeen tutkitaan, suppenevatko kyseiset pinta-alat, niin kutsutut Darboux'n ylä- ja alasumma, toisiinsa.

Riemannin integraalia määritettäessä jaetaan funktion $f(x)$ tutkittava väli osaväleihin, jolloin jakopisteinä ovat $x_{0},x_{1},x_{3}...~jne$, joihin approksimoidaan suorakulmiot. Jakopisteiden tihentyessä infinitesimaalisen välimatkan päähän toisistaan saadaan funktion integraali summaamalla suorakulmiot.

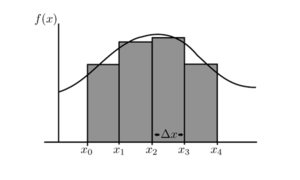
Annetaan nyt muutama määritelmä, joilla saadaan muotoiltua vaadittava osavälien tihentäminen teknisesti. Olkoon $a<b$ ja $n\in \mathbb {N}$. Välin $[a,b]$ $n$-välinen jako on lukujono

$(x_{0},x_{1},\ldots ,x_{n})$,

jolle pätee $x_{i-1}<x_{i}$ kaikilla $1\leq i\leq n$, $x_{0}=a$ ja $x_{n}=b$. Tällöin välit $[x_{i-1},x_{i}]$, missä $1\leq i\leq n$, muodostavat yhteisiä päätepisteitä lukuun ottamatta välin $[a,b]$ osituksen.

Jatkossa jaon merkitsemiseen käytetään symbolia $D_{n}$, ja lisäksi oletetaan, että $D_{n}$ on $k_{n}$-jakoinen, missä siis $(k_{n})_{n\in \mathbb {N} }$ on luonnollisten lukujen jono. Jaon $D_{n}$ jakopisteitä merkitään symbolilla $x_{i}^{n}$, missä $1\leq i\leq k_{n}$, eli toisin sanoen

$D_{n}=(x_{0}^{n},x_{1}^{n},\ldots ,x_{k_{n}}^{n})$.

Jaon $D_{n}$ pisin jakoväli on luku

$|D_{n}|=\max\{x_{i}^{n}-x_{i-1}^{n}\,|\,1\leq i\leq k_{n}\}$.

Jako $D_{i}$ on jaon $D_{j}$ tihennys, jos $D_{j}\subset D_{i}$, eli jaossa $D_{i}$ on vähintään samat jakopisteet kuin jaossa $D_{j}$. Jakojen jono $(D_{1},D_{2},\ldots )$ on tihenevä, jos jokainen jako $D_{i}$ on sitä edeltävän jaon $D_{i-1}$ tihennys.

Riemannin summa ja integraali

Olkoon $D_{n}$ välin $[a,b]$ jako, ja jono

$\xi ^{n}=(\xi _{1}^{n},\ldots ,\xi _{k_{n}}^{n})$

sellainen, että $\xi _{i}^{n}\in [x_{i-1}^{n},x_{i}^{n}]$ kaikilla $1\leq i\leq k_{n}$.

Olkoon $f$ funktio $[a,b]\rightarrow \mathbb {R}$. Funktion $f$ jakoa $D_{n}$ pisteissä $\xi ^{n}$ vastaava Riemannin summa on

$S_{D_{n}}(f,\xi ^{n})=\sum _{i=1}^{k_{n}}f(\xi _{i}^{n})(x_{i}^{n}-x_{i-1}^{n})$.

Riemannin summan jokainen termi vastaa siis sellaisen suorakaiteen etumerkillistä pinta-alaa, jonka kanta on $x_{i}^{n}-x_{i-1}^{n}$ ja korkeus $f(\xi _{i}^{n})$. Se voidaan täten mieltää etsityn pinta-alan likiarvoksi. Likiarvon voisi olettaa tarkentuvan, kun jakoa tihennetään, mutta näin ei välttämättä ole. Esimerkiksi rationaalilukujen joukon indikaattorifunktiolle $1_{\mathbb {Q} }$ voidaan kaikille tiheneville jakojonoille $(D_{n})_{n\in \mathbb {N} }$ valita pisteet $(\xi ^{n})_{n\in \mathbb {N} }$ siten, että vastaava Riemannin summien jono $(S_{D_{n}}(1_{\mathbb {Q} },\xi ^{n}))_{n\in \mathbb {N} }$ ei suppene.

Riemannin integraali määritellään seuraavaksi tihenevän jaon Riemannin summien raja-arvona. Koska raja-arvo ei välttämättä ole olemassa, sanotaan Riemann-integroituviksi niitä funktioita, joilla raja-arvo on olemassa riippumatta pisteiden $\xi ^{n}$ valinnasta.

Olkoon jakojen jono $(D_{n})_{n\in \mathbb {N} }$ tihenevä ja $|D_{n}|\rightarrow 0$, kun $n\rightarrow \infty$. Tämän voi tulkita niin, että jaot hienonevat äärettömän tiheiksi koko välillä $[a,b]$. Sanotaan, että funktion $f$ Riemannin summilla on raja-arvo $S\in \mathbb {R}$, jos jokaiselle luvulle $\varepsilon >0$ on olemassa luvut $\delta _{\varepsilon }>0$ ja $n_{\varepsilon }\in \mathbb {N}$ siten, että

$|S_{D_{n_{\varepsilon }}}(f,\xi ^{n_{\varepsilon }})-S|<\varepsilon$, kun $|D_{n_{\varepsilon }}|<\delta _{\varepsilon }$,

ja $S$ on yksikäsitteinen kaikilla jonolla $\xi ^{n_{\varepsilon }}$. Jos Riemannin summilla on raja-arvo $S$, niin funktio $f$ on Riemann-integroituva välillä $[a,b]$ ja sen Riemannin integraali on luku $S$. Tällöin merkitään

$S=\int _{a}^{b}f(x)\,dx$.

Tässä merkintätavassa funktiota $f$ kutsutaan integrandiksi.

Tämä määritelmä saattaa olla vaikeaselkoinen ja sen käyttäminen monimutkaista. Seuraavaksi määritellään Darboux'n integraali, jonka määritelmä lienee intuitiivisempi ja joka on ominaisuuksiltaan olennaisin osin sama kuin Riemannin integraali.

Darboux'n integraali

Olkoon $f$ reaalifunktio $[a,b]\rightarrow \mathbb {R}$. Funktion $f$ Darboux'n yläsumma jaolla $D_{n}$ on

$S_{D_{n}}(f)=\sum _{i=1}^{k_{n}}(x_{i}^{n}-x_{i-1}^{n})\sup\{f(x)\,|\,x_{i-1}^{n}\leq x\leq x_{i}^{n}\}$.

Vastaava Darboux'n alasumma on

$s_{D_{n}}(f)=\sum _{i=1}^{k_{n}}(x_{i}^{n}-x_{i-1}^{n})\inf\{f(x)\,|\,x_{i-1}^{n}\leq x\leq x_{i}^{n}\}$.

Olkoon jakojen jono $(D_{n})_{n\in \mathbb {N} }$ tihenevä ja $|D_{n}|\rightarrow 0$, kun $n\rightarrow \infty$. Jaon ollessa tihenevä, ovat sekä Darboux'n ylä- että alasummien arvot, eli jonot $(S_{D_{n}}(f))_{n\in \mathbb {N} }$ ja $(s_{D_{n}}(f))_{n\in \mathbb {N} }$, monotonisia. Darboux'n yläintegraali on yläsummien vähenevän jonon infimum, eli luku

$\inf _{n\rightarrow \infty }S_{D_{n}}(f)$.

Darboux'n alaintegraali on puolestaan alasummien kasvavan jonon supremum, eli luku

$\sup _{n\rightarrow \infty }s_{D_{n}}(f)$.

Funktio $f$ on Darboux-integroituva, jos edellä mainitut raja-arvot ovat yhtäläiset eli

$\inf _{n\rightarrow \infty }S_{D_{n}}(f)=\sup _{n\rightarrow \infty }s_{D_{n}}(f)$.

Tällöin kyseistä raja-arvoa kutsutaan funktion $f$ Darboux'n integraaliksi yli välin $[a,b]$.

Funktio on Darboux-integroituva jos ja vain jos se on Riemann-integroituva. Yleinen tapa tarkastaa, onko funktio Riemann-integroituva, onkin verrata sen Darboux'n ylä- ja alaintegraalin arvoja. Lisäksi Darboux'n integraalin arvo on sama kuin Riemannin integraalin, toisin sanoen jos $f$ on Darboux- eli Riemann-integroituva, niin

$\inf _{n\rightarrow \infty }S_{D_{n}}(f)=\int _{a}^{b}f(x)\,dx=\sup _{n\rightarrow \infty }s_{D_{n}}(f)$.

Näistä syistä johtuen Riemannin integraali voidaan periaatteessa määritellä kuten Darboux'n integraali. Joissakin oppikirjoissa esitelläänkin Darboux'n integraali Riemannin integraalina.

Darboux'n ylä- ja alasummat voidaan merkitä myös $U_{f}(P)$ ja $L_{f}(P)$, joissa P on välin jako.

Määritelmän yleistäminen

Riemannin integraali yleistetään mielivaltaiselle integrandin lähtöjoukolle seuraavasti. Olkoon joukko $A$ sellainen, että $[a,b]\subset A\subset \mathbb {R}$, $g$ reaalifunktio $A\rightarrow \mathbb {R}$ ja $g_{[a,b]}:[a,b]\rightarrow \mathbb {R}$ sen rajoittuma välille $[a,b]$. Jos $g_{[a,b]}$ on Riemann-integroituva, niin sanotaan, että $g$ on Riemann-integroituva välillä $[a,b]$, ja funktion $g$ Riemannin integraaliksi yli välin $[a,b]$ määritellään

$\int _{a}^{b}g(x)\,dx=\int _{a}^{b}g_{[a,b]}(x)\,dx$.

Lisäksi määritellään

$\int _{a}^{a}g(x)\,dx=0$

ja

$\int _{a}^{b}g(x)\,dx=-\int _{b}^{a}g(x)\,dx$.

Epäoleellinen integraali

Epäoleellinen integraali on Riemannin integraalien raja-arvo, jossa väli, jonka yli integroidaan, lähestyy joukkoa jossa Riemannin integraali ei ole edellä olevan määritelmän mukaan määritelty. Epäoleellinen integraali voidaan tulkita Riemannin integraalin laajennukseksi, eikä merkinnöissä näille tehdä yleensä eroa.

Ensiksi määritellään epäoleellinen integraali rajoitetulle suljetulle välille tapauksessa, jossa integrandi ei ole määritelty toisessa välin päätepisteessä. Toiseksi määritellään epäoleellinen integraali rajoittamattomalle välille.

Olkoon funktio $f:\ [a,b[\rightarrow \mathbb {R}$ Riemann-integroituva kaikilla väleillä $[a,c]\subset [a,b[$. Jos vasemmanpuoleinen raja-arvo

$\lim _{c\rightarrow b-}\int _{a}^{c}f(x)\,dx$

on olemassa eli reaaliluku, ääretön tai miinus ääretön, niin funktion $f$ epäoleellinen integraali yli välin $[a,b]$ on

$\int _{a}^{b}f(x)\,dx=\lim _{c\rightarrow b-}\int _{a}^{c}f(x)\,dx$.

Funktiolle $]a,b]\rightarrow \mathbb {R}$ epäoleellinen integraali määritellään samoin oikeanpuoleisen raja-arvon kautta.

Olkoon funktio $f:\ [a,\infty [\rightarrow \mathbb {R}$ Riemann-integroituva kaikilla väleillä $[a,c]\subset [a,\infty [$. Jos raja-arvo

$\lim _{c\rightarrow \infty }\int _{a}^{c}f(x)\,dx$

on olemassa, niin funktion $f$ epäoleellinen integraali yli välin $[a,\infty [$ on

$\int _{a}^{\infty }f(x)\,dx=\lim _{c\rightarrow \infty }\int _{a}^{c}f(x)\,dx$.

Samoin määritellään funktiolle $g:\ ]-\infty ,a]\rightarrow \mathbb {R}$

$\int _{-\infty }^{b}f(x)\,dx=\lim _{c\rightarrow -\infty }\int _{c}^{a}f(x)\,dx$.

Ominaisuuksia

Koska Riemannin integraali on määritelty mittateoriasta riippumattomasti, ei se peri kaikkia yleisiä mittaintegraalin ominaisuuksia, vaan ne on johdettava sen määritelmästä analyysin menetelmin. Useimmat niistä ovat johdettavissa, mutta erityisesti konvergenssilauseita ei pysty Riemannin integraalille todistamaan ilman mittateoriaa. Ne ja kaikki muutkin mittaintegraalin ominaisuudet kuitenkin ovat voimassa, sillä Riemannin integraali yhtenee Riemann-integroituville funktioille joidenkin mittaintegraalien kanssa, esimerkiksi Lebesguen integraalin ja Riemann–Stieltjes-integraalin, jonka integraattori on identtinen kuvaus.

Riemann-integroituvia funktioita

Suljetulla välillä jatkuvat funktiot ovat Riemann-integroituvia. Riemann-integroituvien funktioiden summa ja tulo on Riemann-integroituva.

Riemann-integroituvien funktioiden integraalien ominaisuuksia

• Jos$f$ ja $g$ ovat integroituvia välillä [min{a,b},max{a,b}], niin $\int _{a}^{c}f\,dx=\int _{a}^{b}f\,dx+\int _{b}^{c}f\,dx$
• Jos$f$ ja $g$ ovat integroituvia välillä [min{a,b},max{a,b}], niin $\int _{-a}^{a}f\,dx=2\int _{0}^{a}f\,dx,{\mbox{kun }}f(-x)=f(x)$ kaikilla $x\in ]$min$\{a,b\},$max$\{a,b\}[$
• Jos$f$ ja $g$ ovat integroituvia välillä [min{a,b},max{a,b}], niin $\int _{-a}^{a}f\,dx=0,{\mbox{kun }}f(-x)=-f(x)$ kaikilla $x\in ]$min$\{a,b\},$max$\{a,b\}[$

Integraalilaskennan väliarvolauseita

Jos funktio $f$ on Riemann-integroituva välillä $[a,b]$, niin

$\inf _{x\in [a,b]}f(x)\leq {\frac {1}{b-a}}\int _{a}^{b}f(x)\,dx\leq \sup _{x\in [a,b]}f(x)$.

Jos $f$ on jatkuva välillä $[a,b]$, niin on olemassa sellainen $\xi \in ]a,b[$, että

${\frac {1}{b-a}}\int _{a}^{b}f(x)\,dx=f(\xi )$.

Edellä olleita tuloksia kutsutaan integraalilaskennan väliarvolauseiksi. Seuraavia kutsutaan (integraalilaskennan) yleistetyiksi väliarvolauseiksi.

Jos funktiot $f$ ja $g$ ovat Riemann-integroituvia välillä $[a,b]$, $g\geq 0$ ja

$\int _{a}^{b}g(x)\,dx>0$,

niin

$\inf _{x\in [a,b]}f(x)\leq {\frac {\int _{a}^{b}f(x)g(x)\,dx}{\int _{a}^{b}g(x)\,dx}}\leq \sup _{x\in [a,b]}f(x)$.

Jos $f$ on jatkuva välillä $[a,b]$, niin on olemassa sellainen $\xi \in ]a,b[$, että

${\frac {\int _{a}^{b}f(x)g(x)\,dx}{\int _{a}^{b}g(x)\,dx}}=f(\xi )$.

Riemann-integroituvien funktioiden jonojen ominaisuuksia

Nimenomaan funktiojonoja tutkittaessa Riemannin integraalin tekniset puutteet tulevat esiin. Mittateoriassa on käytännöllisiä ja vahvoja konvergenssilauseita, joiden todistaminen on Riemannin integraalille mahdotonta pelkästään analyysin keinoin. Ne pätevät myös Riemannin integraalille, mutta tässä annetaan kaksi ilman mittateoriaa johdettavissa olevaa kaavaa integroimisen ja funktiojonon raja-arvon oton järjestyksen vaihtamiselle. Ne vaativat tasaisen suppenemisen ehdon, mikä on vaativampi ja monimutkaisempi kuin konvergenssilauseiden ehdot, jotka ovat funktiojonon monotonisuus tai funktiojonon rajoittuneisuus. Pelkkä pisteittäinen suppeneminen ei takaa integroimisen ja raja-arvon oton järjestyksen vaihdettavuutta.

Olkoon $(f_{n})_{n\in \mathbb {N} }$ jono Riemann-integroituvia funktioita $[a,b]\rightarrow \mathbb {R}$.

Jos $(f_{n})_{n\in \mathbb {N} }$ suppenee tasaisesti kohti Riemann-integroituvaa funktiota, niin raja-arvon ja integroimisen järjestys voidaan vaihtaa, eli pätee kaava

$\lim _{n\rightarrow \infty }\int _{a}^{b}f_{n}(x)\,dx=\int _{a}^{b}\lim _{n\rightarrow \infty }f_{n}(x)\,dx$.

Jos sarja

$\left(\sum _{n=1}^{k}f_{n}\right)_{k\in \mathbb {N} }$

suppenee tasaisesti kohti Riemann-integroituvaa funktiota, niin summan raja-arvon ja integroimisen järjestys voidaan vaihtaa, eli pätee kaava

$\int _{a}^{b}\sum _{n=1}^{\infty }f_{n}(x)\,dx=\sum _{n=1}^{\infty }\int _{a}^{b}f_{n}(x)\,dx$.

Integraalin arvon määrääminen

Riemannin integraalin arvo voidaan laskea integraalifunktion avulla. Muita yleisiä apukeinoja ovat sijoittaminen eli muuttujanvaihto ja osittaisintegrointi.

Analyysin ensimmäinen peruslause

Analyysin ensimmäinen peruslause antaa yhteyden integraalifunktion ja Riemannin integraalin välille sekä hyvin käytännöllisen tavan Riemannin integraalien laskemiseen. Sen mukaan, jos $f$ on välillä $[a,b]$ jatkuva funktio ja $F$ jokin sen integraalifunktio, niin pätee yhtälö

$\int _{a}^{b}f(x)\,dx=F(b)-F(a)$.

Esimerkki

Analyysin peruslauseen käyttöä voi valaista seuraavalla esimerkillä. Lasketaan Riemannin integraalin

$\int _{0}^{\frac {\pi }{2}}(1+\cos 2t)\,dt$

arvo. Koska funktiolle

$F(t)=t+{\frac {1}{2}}\sin 2t$

pätee

$F'(t)=1+\cos 2t$,

niin analyysin peruslauseesta seuraa tulos

$\int _{0}^{\frac {\pi }{2}}(1+\cos 2t)\,dt$	$=$	$F\left({\frac {\pi }{2}}\right)-F(0)$
	$=$	$\left({\frac {\pi }{2}}+{\frac {1}{2}}\sin \pi \right)-\left(0+{\frac {1}{2}}\sin 0\right)$
	$=$	${\frac {\pi }{2}}$.

Integrointi sijoittamalla

Olkoon $f$ jatkuva funktio reaalivälillä $[a,b]$. Jos $x$ funktio $[\alpha ,\beta ]\rightarrow [a,b]$, jonka derivaatta on jatkuva ja jolle $x(\alpha )=a$ ja $x(\beta )=b$, niin

$\int _{a}^{b}f(x)\,dx=\int _{\alpha }^{\beta }f(x(t))x'(t)\,dt$

Tässä siis muuttujan $x$ tilalle sijoitetaan muuttujan $t$ kuvaus $x(t)$, eli identtisen kuvauksen $x\mapsto x$ tilalle sijoitetaan kuvaus $t\mapsto x(t)$. Tätä kutsutaan Riemannin integraalin muuttujanvaihtokaavaksi. Laskua, jossa etsitään kuvaus $x$ ja sijoitetaan se muuttujanvaihtokaavaan, kutsutaan sijoittamalla integroimiseksi.

Esimerkki

Tyypillistä sijoittamalla integroimista voi kuvata seuraavalla esimerkillä. Riemannin integraalin

$\int _{0}^{1}{\sqrt {1-x^{2}}}\,dx$

laskeminen pelkän analyysin peruslauseen avulla lienee vaikeaa.

Sijoitetaan muuttujan $x$ tilalle kuvaus $t\mapsto \sin(t)$. Nyt edellä olevan kaavan merkinnöin

• $f(x)={\sqrt {1-x^{2}}}$
• $a=0$ ja $b=1$
• $x(t)=\sin(t)$.

Koska

$\sin(0)=0=a$ ja $\sin(\pi /2)=1=b$,

rajoiksi saadaan

$\alpha =0$ ja $\beta =\pi /2$

Sijoittamalla nämä arvot ja $x'(t)=\cos(t)$ muuttujanvaihtokaavaan, saadaan

$\int _{0}^{1}{\sqrt {1-x^{2}}}\,dx=\int _{0}^{\frac {\pi }{2}}{\sqrt {1-\sin ^{2}t}}\ \cos t\,dt$

Tästä voidaan jatkaa ratkaisuun käyttämällä trigonometrisiä kaavoja ja analyysin peruslausetta. Koska $\sin ^{2}t+\cos ^{2}t=1$ saadaan:

${\begin{aligned}\int _{0}^{\frac {\pi }{2}}{\sqrt {1-\sin ^{2}t}}\cos t\,dt&=\int _{0}^{\frac {\pi }{2}}{\sqrt {\cos ^{2}t}}\cos t\,dt\\&=\int _{0}^{\frac {\pi }{2}}|\cos t|\cos t\,dt\end{aligned}}$

Koska kosini on ei-negatiivinen kyseisellä integroimisvälillä, on

$\int _{0}^{\frac {\pi }{2}}|\cos t|\cos t\,dt=\int _{0}^{\frac {\pi }{2}}\cos ^{2}t\,dt$

Sijoittamalla $\cos ^{2}t=1/2(1+\cos 2t)$ seuraa:

$\int _{0}^{\frac {\pi }{2}}\cos ^{2}t\,dt={\frac {1}{2}}\int _{0}^{\frac {\pi }{2}}(1+\cos 2t)\,dt$

Edeltävästä esimerkistä seuraa lopputulos

${\frac {1}{2}}\int _{0}^{\frac {\pi }{2}}(1+\cos 2t)\,dt={\frac {\pi }{4}}$

Osittaisintegrointi

Osittaisintegrointi on operaatio, jonka merkitys riippuu asiayhteydestä, mutta osittaisintegrointikaava Riemannin integraalille pätee seuraavassa muodossa. Olkoon $f$ ja $g$ derivoituvia sekä derivaatat $f'$ ja $g'$ Riemann-integroituvia välillä $[a,b]$. Tällöin

$\int _{a}^{b}f(x)g'(x)\,dx=f(b)g(b)-f(a)g(a)-\int _{a}^{b}f'(x)g(x)\,dx$

Esimerkki

Lasketaan Riemannin integraali osittaisintegroinnilla. On annettu integraali:

$\int _{1}^{2}\ln x\,dx$

Valitaan osittaisintegrointikaavassa

• $\displaystyle f=\ln x$
• $\displaystyle g=x$

Tällöin

• $\displaystyle f'(x)={\frac {1}{x}}$
• $\displaystyle g'(x)=1$

Osittaisintegrointikaavan mukaan:

${\begin{aligned}\int _{1}^{2}\ln x\cdot 1\,dx&=\ln 2\cdot 2-\ln 1\cdot 1-\int _{1}^{2}{\frac {1}{x}}\cdot x\,dx\\&=2\ln 2-0-(2-1)\\&=2\ln 2-1\end{aligned}}$

Sovelluksia

Riemannin integraali soveltuu määritelmänsä kautta luonnollisesti tasokuvioiden pinta-alojen laskemiseen.

Tasokuvion pinta-ala

Tasokuvion, joka jää suorien $x=a$ ja $x=b$ sekä x-akselin ja jatkuvan funktion $f:\ [a,b]\rightarrow \mathbb {R} _{+}$ kuvaajan $y=f(x)$ sisäpuolelle, pinta-ala on

$\int _{a}^{b}f(x)\,dx$.

Funktion f kuvaaja sinisellä, funktion g kuvaaja punaisella ja niiden väliin jäävä tasokuvio vaaleansinisellä

Yleisemmin, jos $f$ ja $g$ ovat jatkuvia funktioita $[a,b]\rightarrow \mathbb {R}$ ja $f>g$, niin niiden kuvaajien sekä suorien $x=a$ ja $x=b$ väliin jäävän tasokuvion pinta-ala on

$\int _{a}^{b}(f(x)-g(x))\,dx$.

Käyrän pituus

Pääartikkeli: Käyrän pituus

Olkoon $f$ tasokuviossa jatkuva käyrä, joka on kuvaus

${\begin{aligned}\left[a,b\right]&\rightarrow \mathbb {R} ^{2}\\t&\mapsto (x(t),\,y(t))\end{aligned}}$

,missä $x$ ja $y$ ovat kuvauksia $[a,b]\rightarrow \mathbb {R}$, joiden derivaatat ovat jatkuvia välillä $[a,b]$. Tällöin käyrän $f$ pituus on:

$\int _{a}^{b}{\sqrt {(x'(t))^{2}+(y'(t))^{2}}}\,dt$

Käyrän pyörähdyskappaleen tilavuus

Jos $f:[a,b]\rightarrow \mathbb {R} _{+}$ on jatkuva funktio, niin suorien $x=a$ ja $x=b$ ja käyrän $y=f(x)$ x-akselin pyörähdyskappaleen tilavuus on

$\pi \int _{a}^{b}(f(x))^{2}\,dx$.

Käyrän pyörähdyskappaleen pinnan ala

Jos $f$ on funktio $[a,b]\rightarrow \mathbb {R} _{+}$, joka on positiivinen välillä $]a,b[$ ja jonka derivaatta on jatkuva välillä $[a,b]$, niin käyrän $y=f(x)$ pyörähtäessä x-akselin ympäri syntyvän kappaleen pinnan ala on

$2\pi \int _{a}^{b}f(x){\sqrt {1+f'(x)^{2}}}\,dx$.

Katso myös

• Henstock-Kurzweil-integraali Riemannin integraalin yleistys

Kirjallisuutta

• Pitkäranta, Juhani: Calculus Fennicus – TKK:n 1. lukuvuoden laaja matematiikka (2000–2013) (pdf) Helsinki: Avoimet oppimateriaalit ry. ISBN 978-952-7010-12-9 ISBN 978-952-7010-6 (pdf). Viitattu 8.7.2019.

Aiheesta muualla

• MathWorld. Darboux Integral
  • MathWorld. Lower Sum
  • MathWorld. Upper Sum
  • MathWorld. Lower Integral
  • MathWorld. Upper Integral
• MathWorld. Riemann Sum
• MathWorld. Riemann Integral
• MathWorld. Improper Integral
• MathWorld. Integration by Parts