Luonnollinen logaritmi

Luonnollisen logaritmifunktion kuvaaja. Funktio kasvaa hitaasti, mutta rajattomasti, kun x kasvaa, ja sen raja-arvo, kun x lähestyy nollaa, on miinus ääretön. Näin ollen y-akseli on kuvaajan asymptootti.

Luonnollinen logaritmi on logaritmifunktio, jonka kantaluku on Neperin luku e, eräs irrationaalinen ja transsendenttinen matemaattinen vakio, likiarvoltaan 2,718 281 828. Luvun x luonnollinen logaritmi voidaan merkitä log_e x, mutta tavallisesti sille käytetään merkintää ln x, joskus myös yksinkertaisesti log x. Selvyyden vuoksi merkintään liitetään toisinaan sulku­merkit: ln(x), log_e(x) tai log(x) Näin menetellään varsinkin, jos funktion argumenttina ei ole yksittäinen luku tai symboli vaan lauseke.

Luvun x luonnollinen logaritmi on se eksponentti, jonka osoittamaan potenssiin e on korotettava, jotta saadaan luku x. Esimerkiksi ln 7,5 on noin 2,0149, koska e^2,0149 on noin 7,5. Neperin luvun e luonnollinen logaritmi on ln e = 1, koska e¹ = e, ja ln 1 = 0, koska e⁰ = 1.

Luonnollinen logaritmifunktio on siis eksponenttifunktion e^x käänteisfunktio, jolle pätevät:

$e^{\ln(x)}=x\qquad$

$\ln(e^{x})=x.\,\!$,

ylempi näistä edellyttäen, että x > 0.

Luonnollinen logaritmi on määritelty kaikille positiivisille reaali­luvuille. Luvun a luonnollinen logaritmi voitaisiin yhtäpitävästi määritellä myös sen alueen pinta-alana, joka jää x-akselin, käyrän y = 1/x sekä suorien x = 1 ja 'x = a väliin, tai jos a < 1, tämän pinta-alan vastalukuna. Tämän määritelmän yksinkertaisuus sekä monet muut kaavat, joissa luonnollinen logaritmi esiintyy, ovat johtaneet siihen, että sitä on alettu nimittään "luonnolliseksi".

Luonnollisen logaritmin määritelmää voidaan laajentaa niin, että logaritmi voidaan ottaa myös negatiivisista luvuista ja kaikista kompleksi­luvuista nollaa lukuun ottamatta, joskin tällöin logaritmista tulee moniarvoinen funktio.

Kaikkien logaritmien tavoin luonnolliselle logaritmille pätee, että kahden luvun tulon logaritmi on lukujen logaritmien summa:

$\ln(xy)=\ln(x)+\ln(y).\!\,$

Täten logaritmi tavallaan muuntaa kertolaskun yhteenlaskuksi. Logaritmifunktio onkin isomorfismi positiivisten reaalilukujen ryhmästä, jossa laskutoimituksena on kertolasku, kaikkien reaalilukujen ryhmälle, jossa laskutoimituksena on yhteenlasku:

$\ln \colon \mathbb {R} ^{+}\to \mathbb {R} .$

Logaritmifunktion kantalukuna voi olla, paitsi e, mikä tahansa muukin positiivinen reaaliluku, ei kuitenkaan luku 1. Eri logaritmifunktioita erottaa toisistaan kuitenkin vain vakiokerroin, ja muut logaritmit määritelläänkin usein luonnollisen logaritmin avulla:

log_b a = ln a / ln b.

Esimerkiksi jokaisen luvun binäärinen eli kaksi­kantainen logaritmi saadaan jakamalla luvun luonnollinen logaritmi luvulla ln 2, luvun 2 luonnollisella logaritmilla ja vastaavasti Briggsin eli kymmen­kantainen logaritmi jakamalla luonnollinen logaritmi luvulla ln 10.

Logaritmeja tarvitaan sellaisten yhtälöiden ratkaisemiseen, joiden eksponentissa esiintyy tuntematon. Niitä sovelletaan varsinkin tapauksiin, joissa jokin suure kasvaa tai vähenee eksponentiaalisesti jonkin toisen suureen, esimerkiksi ajan funktiona. Niillä on runsaasti sovelluksia luonnon­tieteissä ja myös monissa taloudellisissa yhteyksissä kuten koron­korkoon liittyvissä laskuissa.

Luonnollinen logaritmi
Merkintä	$\ln x\,$
Käänteisfunktio	$e^{x}\,$
Derivaatta	${\frac {1}{x}}\,$
Integraalifunktio	$x\ln x-x+C\,$

Historia

Luonnollisen logaritmin käsitteen ottivat käyttöön Gregoire de Saint-Vincent ja Alphonse Antonio de Sarasa ennen vuotta 1649. He tutkivat hyperbelin $xy=1$ rajoittaman alueen neliöimistä eli sen pinta-alan määrittämistä. Ratkaistaakseen tehtävän he määrittelivät "hyperboliseksi logaritmiksi" nimittämänsä funktion, joka oli käytännössä sama, jota nykyisin sanotaan luonnolliseksi logaritmiksi.

Eräs varhainen maininta luonnollisesta logaritmistä sisältyy Nicholas Mercatorin vuonna 1668 julkaistuun teokseen Logarithmotechnia, joskin matemaatikko John Speidell oli jo vuonna 1619 laatinut taulukon arvoista, jotka käytännössä olivat lukujen luonnollisia logaritmeja.

Luonnollista logaritmia nimitetään toisinaan myös Napierin logaritmiksi John Napierin mukaan, vaikka Napierin alun perin käyttämien logaritmien kantaluku poikkesi jonkin verran Neperin luvusta e.

Merkintätapoja

Merkinnät "ln x" ja "log_e x" tarkoittavat molemmat yksi­selitteisesti luvun x luonnollista logaritmia.

Myös merkintää "log x", jossa kanta­lukua ei ole ilmoitettu, käytetään toisinaan tarkoittamaan luonnollista logaritmia. Tämä käytäntö on tavallinen matematiikassa ja joissakin tieteellisissä yhteyksissä, ja sitä noudatetaan myös monissa ohjelmointikielissä (esimerkiksi C, C++, SAS, MATLAB, Mathematica, Fortran ja BASIC). Eräissä muissa yhteyksissä "log x" saattaa kuitenkin tarkoittaa myös kymmen­kantaista eli Briggsin logaritmia.

Luonnollisen logaritmin erityisominaisuuksia ja nimityksen alkuperä

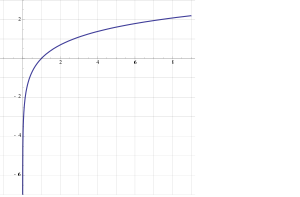
Tämän sivun alussa oleva luonnollisen logaritmifunktion kuvaaja ilmentää joitakin ominaisuuksia, jotka ovat yhteisiä kaikille logaritmifunktioille kantaluvusta riippumatta. Tärkeimpiä niistä ovat: luvun 1 logaritmi on 0, ja luvun lähestyessä 0:aa sen logaritmi lähestyy -∞:tä. Luonnollisen logaritmin erikois­asema ilmenee parhaiten ehkä siinä pisteessä, jossa logaritmi on kaikilla kantaluvuilla nolla, nimittäin luvun 1 kohdalla. Siinä kohdassa nimittäin luonnollisen logaritmin, ja vain sen, kuvaajan kulmakerroin on myös 1, toisin sanoen kuvaaja leikkaa x-akselin 45 asteen kulmassa. Jos logaritmi­funktion kanta­luku on suurempi kuin e, kuten on esimerkiksi 10-kantaisen eli Briggsin logaritmin laita, kulma­kerroin on tässä kohdassa pienempi kuin 1, ja jos kantaluku on pienempi kuin e, kuten esimerkiksi 2-kantaisella logaritmilla, kulma­kerroin on tässä kohdassa suurempi kuin 1. Kaikkien menetelmien, joilla luvulle e tai luonnollisille logaritmeille voidaan laskea likiarvoja, voidaan katsoa perustuvan viime kädessä juuri tähän ominaisuuteen. Tästä seuraa myös, että kun annettu luku on tarpeeksi lähellä lukua 1, sen luonnolliselle logaritmille saadaan hyvä likiarvo yksin­kertaisesti vähentämällä luvusta 1. Esimerkiksi luvun 1,01 luonnollinen logaritmi on noin 0,00995 eli noin viiden tuhannesosan tarkkuudella 0,01. Samaan tapaan voidaan todeta, että luvun 0,99 luonnollinen logaritmi on hyvin lähellä lukua -0,01. Tämä pätee sitä tarkemmin, mitä lähempänä yhtä alku­peräinen luku on. Samassa mielessä kuin luku 1 itse on yhteinen kaikille lukujärjestelmille, voidaan luonnollista logaritmia pitää luku­järjestelmästä riippumattomana. Tämän erikois­asemansa vuoksi tätä logaritmi­funktiota on alettu nimittää "luonnolliseksi" (lat. naturalis, engl. natural).

Voisi ajatella, että koska kymmenjärjestelmä on yleis­maailmallisesti käytetty lukujärjestelmä, luku 10 olisi "luonnollisempi" myös logaritmi­järjestelmän kanta­luvuksi. Kymmen­kantaisia eli Briggsin logaritmeja ja niistä koottuja taulukoita onkin ennen taskulaskinten yleistymistä paljon käytetty lasku­toimitusten apu­välineenä. Matemaattisesti luku 10 ei kuitenkaan ole mitenkään erikois­asemassa. Todennäköisesti sen asema luku­järjestelmän kantal­ukuna onkin saanut alkunsa sormilla laskemisesta ja siten ihmisen sormien luku­määrästä. Joissakin kulttureissa on käytetty myös muita luku­järjestelmiä, joiden kanta­lukuina ovat olleet esimerkiksi 5, 8, 12, 20 tai 60.

Funktio log_e on "luonnollinen" logaritmi, koska se esiintyy matematiikassa luonnostaan monissa yhteyksissä. Tarkastellaan esimerkiksi logaritmi­funktioiden derivaattoja:

${\frac {d}{dx}}\log _{b}(x)={\frac {d}{dx}}\left({\frac {1}{\ln(b)}}\ln {x}\right)={\frac {1}{\ln(b)}}{\frac {d}{dx}}\ln {x}={\frac {1}{x\ln(b)}}.$

Jos kantaluvuksi b valitaan e, derivaatta on yksin­kertaisesti 1/x, ja pisteessä x = 1 derivaatta saa arvon 1. Toinen syy, jonka vuoksi e-kantaista logaritmia voidaan pitää luonnollisimpana, on, että se voidaan varsin helposti määritellä yksin­kertaisena integraalina tai Taylorin sarjana, mikä ei ole mahdollista muille logaritmi­funktioille.

Luonnollisen logaritmin "luonnollisuus" ei kuitenkaan liity yksinomaan differentiaali- ja integraalilaskentaan. Esimerkiksi on olemassa monia yksin­kertaisia sarjoja, jotka johtavat luonnolliseen logaritmiin. Pietro Mengoli ja Nicholas Mercator käyttivätkin siitä nimitystä logaritmhmus naturalis jo vuosikymmeniä ennen kuin Newton ja Leibniz kehittivät differentiaali- ja integraalilaskennan.

Määritelmiä

X-akselin, suorien x = 1 ja x=a sekä käyrän y = 1/x välisen alueen pinta-ala on ln a. Jos a on pienempi kuin 1, ln a on kuitenkin negatiivinen ja alueen pinta-ala on sen positiivinen vastaluku -ln a.

Muodollisesti ln(a) voidaan määritellä integraalina,

$\ln(a)=\int _{1}^{a}{\frac {1}{x}}\,dx.$

Tämä funktio on logaritmi, koska se toteuttaa logaritmien perusominaisuuden:

$\ln(ab)=\ln(a)+\ln(b).\,\!$

Tämä voidaan osoittaa jakamalla ln(ab):n määrittelevä integraali osiin ja suorittamalla jälkimmäisessä muuttujan vaihto x = ta seuraavasti:

${\begin{aligned}\ln(ab)=\int _{1}^{ab}{\frac {1}{x}}\;dx&=\int _{1}^{a}{\frac {1}{x}}\;dx\;+\int _{a}^{ab}{\frac {1}{x}}\;dx\\&=\int _{1}^{a}{\frac {1}{x}}\;dx\;+\int _{1}^{b}{\frac {1}{at}}\;d(at)\\&=\int _{1}^{a}{\frac {1}{x}}\;dx\;+\int _{1}^{b}{\frac {1}{t}}\;dt\\&=\ln(a)+\ln(b).\end{aligned}}$

Luku e voidaan tämän jälkeen määritellä ainoaksi reaaliluvuksi a, jolla ln(a) = 1.

Vaihtoehtoisesti voidaan eksponenttifunktio määritellä ensin, esimerkiksi päättymättömän sarjan avulla, jolloin luonnollinen logaritmi voidaan määritellä sen käänteisfunktiona, toisin sanoen ln on funktio, jolle pätee exp(ln(x)) = x. Koska eksponentti­funktion arvojoukko käsittää kaikki positiiviset reaali­luvut ja koska se on aidosti kasvava, luonnollinen logaritmi on tällöin hyvin määritelty kaikille positiivisille argumentin arvoille.

Ominaisuuksia

• $\ln(1)=0\,$
• $\ln(-1)=i\pi \,$ katso osiota #Kompleksinen logaritmi
• $\ln(x)<\ln(y)\quad {\rm {for}}\quad 0<x<y\,$
• $\lim _{x\to 0}{\frac {\ln(1+x)}{x}}=1\,$
• $\ln(x^{y})=y\,\ln(x)\,$
• ${\frac {x-1}{x}}\leq \ln(x)\leq x-1\quad {\rm {for}}\quad x>0\,$
• $\ln {(1+x^{\alpha })}\leq \alpha x\quad {\rm {for}}\quad x\geq 0,\alpha \geq 1\,$

Todistus

Lause on tosi, kun $x=0$, ja osoitamme, että ${\frac {d}{dx}}\ln {(1+x^{\alpha })}\leq {\frac {d}{dx}}(\alpha x)$ kaikille $x$, jolloin todistuksen täydentää analyysin peruslause. Yritämme siis todistaa, että

${\frac {d}{dx}}\ln {(1+x^{\alpha })}={\frac {\alpha x^{\alpha -1}}{1+x^{\alpha }}}\leq \alpha ={\frac {d}{dx}}(\alpha x)$

(Emme kuitenkaan ole vielä osoittaneet tätä todeksi). Jos tämä kaksoisepäyhtälö pätee, kertomalla keskimmänen lauseke positiivisella lausekkeella $(1+x^{\alpha })/\alpha$ ja vähentämällä $x^{\alpha }$ saataisiin

$x^{\alpha -1}\leq x^{\alpha }+1$

$x^{\alpha -1}(1-x)\leq 1$

Tämä pätee tietenkin, jos $x\geq 1$ sillä vasen puoli on tällöin negatiivinen tai nolla. Se pätee myös, kun $0\leq x<1$, sillä vasemmalla puolella molemmat tekijät ovat pienempiä kuin 1, sillä $\alpha \geq 1$). Niinpä jälkimmäinen lause on tosi, ja toistamalla samat askelet päinvastaisessa järjestyksessä todetaan, että

${\frac {d}{dx}}\ln {(1+x^{\alpha })}\leq {\frac {d}{dx}}(\alpha x)$ kaikilla $x$:n arvoilla. mot.

Derivaatta ja Taylorin sarjat

Luonnollisen logaritmin derivaatta on

${\frac {d}{dx}}\ln(x)={\frac {1}{x}}.\,$

Tästä saadaan muodostetuksi luonnollisen logaritmin ln(1 + x) Taylorin sarja nollan läheisyydessä:

$\ln(1+x)=\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}x^{n}=x-{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}-\cdots \quad {\rm {for}}\quad \left|x\right|\leq 1,\quad$

joka pätee välillä -1 < x ≤ 1.

Tätä nimitetään myös Mercatorin sarjaksi.

Leonhard Euler yritti rohkeasti soveltaa tätä sarjakehitelmää myös arvolle x = -1 osoittaakseen, että harmonisen sarjan summa on yhtä kuin ln (1/(1-1)), siis äärettömän luonnollinen logaritmi. Nykyisin tätä todistusta ei pidetä pätevänä. Sen sijaan voidaan kyllä todistaa, että mitä suurempi luku N on, sitä lähempänä harmonisen sarjan ensimmäisten N termin summan ja N:n luonnollisen logaritmin erotus on niin sanottua Eulerin–Mascheronin vakiota, jonka likiarvo on 0,57721566490153286061.

ln(1 + x):n Taylorin polynomit antavat hyviä likiarvoja vain välillä −1 < x ≤ 1. Huomattava että kun x > 1, korkeammat Taylorin polynomit ovat huonompia likiarvoja.

Oikealla olevassa kaaviossa on funktion ln(1 + x) ja sen joidenkin Taylorin polynomien kuvaajat nollan ympäristössä. Nämä antavat likiarvoja, jotka suppenevat kohti funktiota ln(1 + x) ainoastaan välillä −1 < x ≤ 1; tämän välin ulkopuolella Taylorin sarja hajaantuu ja korkeammat Taylorin polynomit antavat vain huonompia likiarvoja itse funktiolle.

Jos x:n tilalle vaihdetaan ''x − 1, saadaan vaihtoehtoinen esitys ln(x):lle itselleen, nimittäin

$\ln(x)=\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}(x-1)^{n}$

$\ln(x)=(x-1)-{\frac {(x-1)^{2}}{2}}+{\frac {(x-1)^{3}}{3}}-{\frac {(x-1)^{4}}{4}}\cdots$

${\rm {for}}\quad \left|x-1\right|\leq 1\quad {\rm {unless}}\quad x=0\,.$

Soveltamalla Mercatorin sarjaan Eulerin muunnosta saadaan seuraava sarjakehitelmä, joka pätee kaikilla x:n arvoilla, joiden itseisarvo on suurempi kuin 1:

$\ln {x \over {x-1}}=\sum _{n=1}^{\infty }{1 \over {nx^{n}}}={1 \over x}+{1 \over {2x^{2}}}+{1 \over {3x^{3}}}+\cdots \,.$

Tämä sarja muistuttaa BBP-tyypin kaavaa.

On myös huomattava, että $x \over {x-1}$ on itsensä käänteisfunktio, ja niinpä annetun luvun y luonnollinen logaritmi voidaan saada korvaamalla x lausekkeella $y \over {y-1}$. Tällä tavoin voidaam muodostaa sarjakehitelmä

$\ln {x}=\sum _{n=1}^{\infty }{1 \over {n}}\left({x-1 \over x}\right)^{n}=\left({x-1 \over x}\right)+{1 \over 2}\left({x-1 \over x}\right)^{2}+{1 \over 3}\left({x-1 \over x}\right)^{3}+\cdots \,$

joka pätee, kun ${\rm {for}}\quad \operatorname {Re} (x)\geq {\frac {1}{2}}\,.$

Luonnollinen logaritmi integraalilaskennassa

Luonnollisen logaritmin avulla voidaan helposti integroida muotoa g(x) = f '(x)/f(x) olevat funktiot: funktion g(x) eräs integraalifunktio on ln(|f(x)|). Tämä perustuu ketjusääntöön ja siihen, että

$\ {d \over dx}\left(\ln \left|x\right|\right)={1 \over x}.$

Toisin sanoen

$\int {1 \over x}dx=\ln |x|+C$

ja

$\int {{\frac {f'(x)}{f(x)}}\,dx}=\ln |f(x)|+C.$

Esimerkkinä voidaan mainita tapaus, jossa g(x) = tan(x):

$\int \tan(x)\,dx=\int {\sin(x) \over \cos(x)}\,dx$

$\int \tan(x)\,dx=\int {-{d \over dx}\cos(x) \over {\cos(x)}}\,dx.$

Letting f(x) = cos(x) and f'(x)= – sin(x):

$\int \tan(x)\,dx=-\ln {\left|\cos(x)\right|}+C$

$\int \tan(x)\,dx=\ln {\left|\sec(x)\right|}+C$

missä C on mielivaltainen integroimisvakio.

Itse luonnollisen logaritmin integraalifunktio saadaan osittaisintegroinnilla:

$\int \ln(x)\,dx=x\ln(x)-x+C.$

Likiarvojen laskenta

Annetun luvun luonnollisen logaritmin laskemiseksi Taylorin sarja voidaan muuntaa muotoon:

$\ln(1+x)=x\,\left({\frac {1}{1}}-x\,\left({\frac {1}{2}}-x\,\left({\frac {1}{3}}-x\,\left({\frac {1}{4}}-x\,\left({\frac {1}{5}}-\cdots \right)\right)\right)\right)\right)\quad {\rm {for}}\quad \left|x\right|<1.\,\!$

Jotta saataisiin nopeammin suppeneva sarja, voidaan käyttää seuraavia identiteettejä:

${\begin{aligned}\ln(x)=\ln \left({\frac {1+y}{1-y}}\right)&=2\,y\,\left({\frac {1}{1}}+{\frac {1}{3}}y^{2}+{\frac {1}{5}}y^{4}+{\frac {1}{7}}y^{6}+{\frac {1}{9}}y^{8}+\cdots \right)\\&=2\,y\,\left({\frac {1}{1}}+y^{2}\,\left({\frac {1}{3}}+y^{2}\,\left({\frac {1}{5}}+y^{2}\,\left({\frac {1}{7}}+y^{2}\,\left({\frac {1}{9}}+\cdots \right)\right)\right)\right)\right)\end{aligned}}$

edellyttäen, että y = (x−1)/(x+1) ja Re(x) ≥ 0 mutta x ≠ 0.

Kun x > 1; tämä sarja suppenee sitä nopeammin, mitä lähempänä x on arvoa 1. Logaritmin laskemiseksi suurista luvuista voidaan käyttää seuraavanlaista apukeinoa, esimerkiksi:

${\begin{aligned}\ln(123.456)&=\ln(1.23456\times 10^{2})\\&=\ln(1.23456)+\ln(10^{2})\\&=\ln(1.23456)+2\times \ln(10)\\&\approx \ln(1.23456)+2\times 2.3025851.\end{aligned}}$

Tällaisia apukeinoja käytettiin varsinkin ennen nykyaikaisten laskinten aikaa: pienten lukujen logaritmit katsottiin taulukosta ja suuret luvut muunnettiin pienen luvun ja jonkin 10:n potenssin tuloksi.

Luvun 10 luonnollinen logaritmi

Luvun 10 luonnollinen logartimi on desimaalilukuna 2,30258509..., Tätä voidaan käyttää hyväksi laskettaessa arvoja hyvinkin suurten lukujen luonnollisille logaritmeille. Tällaiset luvut esitetään usein kymmenpotenssimuodossa, jolloin pätee:

$\ln(a\times 10^{n})=\ln a+n\ln 10.$

Hyvin suurten ja hyvin pienten lukujen luonnolliset logaritmit voidaan näin laskea käyttämällä taulukkoja, joissa ovat ainoastaan välillä $[1,10)$ olevien lukujen luonnolliset logaritmit.

Suuri tarkkuus

Luonnollisen logaritmin laskemiseen monen desimaalin tarkkuudella ei Taylorin sarja ole tehokas, koska se suppenee hitaasti. Jos x on lähellä 1:tä, vaihtoehtoinen tapa on käyttää Newtonin menetelmää eksponenttifunktion kääntämiseksi, sillä eksponenttifunktion sarja suppenee nopeammin. Parhaiten valitulla funktiolla iteraatio yksinkertaistuu muotoon

$y_{n+1}=y_{n}+2\cdot {\frac {x-\exp(y_{n})}{x+\exp(y_{n})}}\,$

joka suppenee kuutiollisesti kohti arvoa ln(x).

Toinen keino erittäin suuren tarkkuuden saamiseksi on kaava

$\ln x\approx {\frac {\pi }{2M(1,4/s)}}-m\ln 2,$

missä M tarkoittaa lukujen 1 ja 4/s aritmeettis-geometrista keskiarvoa ja

$s=x\,2^{m}>2^{p/2},$

missä m valitaan niin, että saavutetaan p bitin tarkkuus. Useimpiin tarkoituksiin riittää arvo m = 8. Itse asiassa tämän tuloksen avulla voidaan Newtonin menetelmää käyttää eksponentti­funktion arvojen tehokkaaseen laskentaan. Vakiot ln 2 ja π on laskettava ennalta halutulla tarkkuudella käyttämällä jotakin niille kehitetyistä nopeasti suppenevista sarjoista.

Ketjumurtolukuesitys

Vaikka luonnolliselle logaritmille ei ole yksinkertaista ketjumurtolukuesitystä, se voidaan muodostaa useammallakin tavalla yleistettynä ketju­murto­lukuna, esimerkiksi:

$\ln(1+x)={\frac {x^{1}}{1}}-{\frac {x^{2}}{2}}+{\frac {x^{3}}{3}}-{\frac {x^{4}}{4}}+{\frac {x^{5}}{5}}-\cdots ={\cfrac {x}{1-0x+{\cfrac {1^{2}x}{2-1x+{\cfrac {2^{2}x}{3-2x+{\cfrac {3^{2}x}{4-3x+{\cfrac {4^{2}x}{5-4x+\ddots }}}}}}}}}}$

$\ln \left(1+{\frac {x}{y}}\right)={\cfrac {x}{y+{\cfrac {1x}{2+{\cfrac {1x}{3y+{\cfrac {2x}{2+{\cfrac {2x}{5y+{\cfrac {3x}{2+\ddots }}}}}}}}}}}}={\cfrac {2x}{2y+x-{\cfrac {(1x)^{2}}{3(2y+x)-{\cfrac {(2x)^{2}}{5(2y+x)-{\cfrac {(3x)^{2}}{7(2y+x)-\ddots }}}}}}}}$

Nämä ketjumurtoluvut, varsinkin jälkimmäinen, suppenevat nopeasti lähellä 1:tä olevilla arvoilla. Paljon suurempienkien lukujen luonnolliset logaritmit voidaan helposti saada laskemalla yhteen pienempien lukujen logaritmeja, joiden ketju­murto­luku­esitykset suppenevat nopeasti.

Esimerkiksi, koska 2 = 1x25³ · 1,024, voidaan luvun 2 luonnollinen logaritmi laskea seuraavasti:

$\ln 2=3\ln \left(1+{\frac {1}{4}}\right)+\ln \left(1+{\frac {3}{125}}\right)={\cfrac {6}{9-{\cfrac {1^{2}}{27-{\cfrac {2^{2}}{45-{\cfrac {3^{2}}{63-\ddots }}}}}}}}+{\cfrac {6}{253-{\cfrac {3^{2}}{759-{\cfrac {6^{2}}{1265-{\cfrac {9^{2}}{1771-\ddots }}}}}}}}.$

Vastaavasti koska 10 = 1,25¹⁰ · 1,024³, voidaan myös luvun 10 luonnollinen logaritmi laskea samaan tapaan:

$\ln 10=10\ln \left(1+{\frac {1}{4}}\right)+3\ln \left(1+{\frac {3}{125}}\right)={\cfrac {20}{9-{\cfrac {1^{2}}{27-{\cfrac {2^{2}}{45-{\cfrac {3^{2}}{63-\ddots }}}}}}}}+{\cfrac {18}{253-{\cfrac {3^{2}}{759-{\cfrac {6^{2}}{1265-{\cfrac {9^{2}}{1771-\ddots }}}}}}}}.$

Kompleksinen logaritmi

Eksponenttifunktio voidaan laajentaa kompleksilukujen joukkoon niin, että jokaiselle kompleksiluvuille z saadaan funktion arvo e^z samalla Taylorin sarjalla kuin reaaliluvuillekin. Tämän laajennetun funktion käänteisfunktiona voidaan kompleksi­luvuille määritellä myös luonnollinen logaritmi, jolla pätevät useimmat reaalisen luonnollisen logaritmin ominaisuudet. Kaksi seikkaa aiheuttaa kuitenkin vaikeuksia: ensinnäkään millekään luvulle z ei ole e^z = 0, ja toiseksi osoittauutuu, että e^2πi = 1 = e⁰. Koska kerto­lasku­ominaisuus kuitenkin toimii kompleksisellakin eksponentti­funktiolla, on

e^z = e^z+2nπi

kaikilla kompleksiluvuilla z ja kokonaisluvuilla n.

Näin ollen logaritmia ei voida määritellä koko kompleksitasossa, ja määrittelyjoukossaankin sen on moniarvoinen: jokaiseen kompleksiluvun logaritmi voidaan muuntaa toiseksi saman kompleksiluvun logaritmiksi lisäämällä siihen mielivaltainen 2πi:n monikerta. Esimerkiksi ln i = 1/2 πi, 5/2 πi tai −3/2 πi jne, ja vaikka i⁴ = 1, voidaan määritellä, että 4 log i on 2πi, 10πi tai −6πi ja niin edelleen. Kompleksinen logaritmi voidaan kuitenkin määritellä yksiarvoisena jatkuvana funktiona jokaisessa sellaisessa kompleksitason yhdesti yhtenäisessä alueessa, johon origo ei sisälly. Tällöin valitaan alueesta jokin piste ja jokin kyseistä pistettä vastaavan luonnollisen logaritmifunktion arvoista funktion arvoksi. Tällöin on olemassa yksi ja vain yksi sellainen yksiarvoinen jatkuva funktio, jonka arvo kaikissa kyseisen alueen pisteissä on jokin pistettä vastaavan kompleksiluvun luonnollisen logaritmin arvoista. Tämä funktio on myös analyyttinen kyseisessä alueessa.

Kompleksitason yhdesti yhtenäisiä alueita, joissa luonnollinen logaritmi voidaan tällä tavoin yksikäsitteisesti määritellä, ovat esimerkiksi sellaiset kiekot, joihin origo ei sisälly, sekä myös alueet, jotka saadaan poistamalla tasosta ainoastaan jokin origosta alkava puolisuora, joka tällöin ei sisälly alueeseen. Usein tällaiseksi puolisuoraksi valitaan negatiivinen reaaliakseli, jolloin jäljelle jäävän alueen jokaisen luvun luonnollisella logaritmilla on sellainen arvo, jonka imaginääriosa y on välillä $-\pi <y<\pi$. Tätä sanotaan logaritmin päähaaraksi, ja sille käytetään merkintää Log z.

• Luonnollisen logaritmin päähaaran graafisia esityksiä kompleksitasossa
• 
  z = Re(ln(x+iy))
• 
  z = $\textstyle \left\vert \operatorname {Im} (\ln(z))\right\vert$
• 
  z = $\textstyle \left\vert \ln(z)\right\vert$
• 
  Kolmen edellistä kuvaajaa yhdistettyinä

Kirjallisuutta

• Rikkonen, Harri: Matematiikan pitkä peruskurssi II: Reaalimuuttujan funktioiden differentiaalilasku. Helsinki: Otakustantamo, 1969. ISBN 951-671-022-0.
• Pitkäranta, Juhani: Calculus Fennicus – TKK:n 1. lukuvuoden laaja matematiikka (2000–2013) (pdf) Helsinki: Avoimet oppimateriaalit ry. ISBN 978-952-7010-12-9 ISBN 978-952-7010-6 (pdf).

Aiheesta muualla

• Demystifying the Natural Logarithm (ln) | BetterExplained