Newtonin menetelmä
Newtonin menetelmä (tunnettu myös nimillä Newtonin–Raphsonin menetelmä tai Newtonin–Fourier'n menetelmä) on numeerisessa analyysissä tehokas algoritmi funktion nollakohtien likiarvojen löytämiseksi. Sitä voidaan käyttää myös funktion ääriarvojen etsimiseen soveltamalla menetelmää funktion ensimmäiseen derivaattaan.
Menetelmän kuvaus[muokkaa | muokkaa wikitekstiä]
Aloitetaan nollakohdan etsiminen tekemällä tuntemattomalle alkuarvaus mieluiten mahdollisimman läheltä haluttua nollakohtaa. Korvataan funktio tangentillaan, mikä voidaan tehdä lukiomatematiikan keinoinselvennä. Tämän jälkeen lasketaan kyseisen tangentin nollakohta. Yleensä tämä nollakohta on parempi likiarvo funktion nollakohdalle. Otetaan tämä uudeksi arvoksi ja toistetaan iterointi riittävän usein haluttuun tarkkuuteen pääsemiseksi.
Oletetaan, että f : [a, b] → R on derivoituva funktio, joka on määritelty välillä [a, b] ja sen arvojoukko koostuu reaaliluvuista R. Nollakohta löydetään seuraavasti. Oletetaan, että tiedossa oleva likiarvo on xn. Siitä saadaan parempi likiarvo xn+1 alla olevan diagrammin mukaisesti. Derivaatan määritelmästä tunnetaan, että derivaatan arvo missä tahansa pisteessä on kyseiseen pisteeseen piirretyn tangentin kulmakerroin.
Tällöin
- .
Tässä f ' tarkoittaa funktion f derivaattaa. Tästä päädytään sieventämällä muotoon
- .
Iterointi aloitetaan valitsemalla jokin näennäisen satunnainen alkuarvo x0 (mitä lähempää todellista nollakohtaa tämä valitaan, yleensä sitä parempi). Menetelmä yleensä suppenee, mikäli valittu alkuarvo on riittävän lähellä nollakohtaa. Karkeasti voidaan todeta, että nollakohdan ympäristössä saadun likiarvon oikeiden desimaalien lukumäärä vähintään kaksinkertaistuu jokaisessa iteraatiossa.
Kuva Newtonin menetelmän yhdestä iteraatiosta. Tästä nähdään, että on funktion nollakohdalle parempi likiarvo kuin
Esimerkki[muokkaa | muokkaa wikitekstiä]
Etsi yhtälön cos(x) = x3 positiivinen ratkaisu. Muutetaan tehtävä funktion f(x) = cos(x) − x3 nollakohdan löytämiseksi. Derivoidaan funktio: f '(x) = −sin(x) − 3x2. Koska cos(x) ≤ 1 kaikille x:n arvoille ja x3 > 1, kun x > 1, tiedämme, että nollakohta on välillä ]0,1[. Otetaan alkuarvoksi x0 = 0,5.
Oikeat desimaalit on yllä olevassa esimerkissä alleviivattu. x6:n kaikki merkityt desimaalit ovat oikeita. Voidaan huomata, että pilkun jälkeisten oikeiden desimaalien lukumäärä kasvaa x3:n kahdesta viiteen ja sitten kymmeneen.
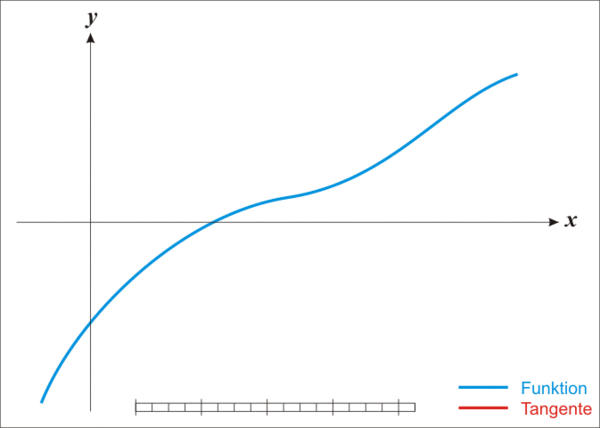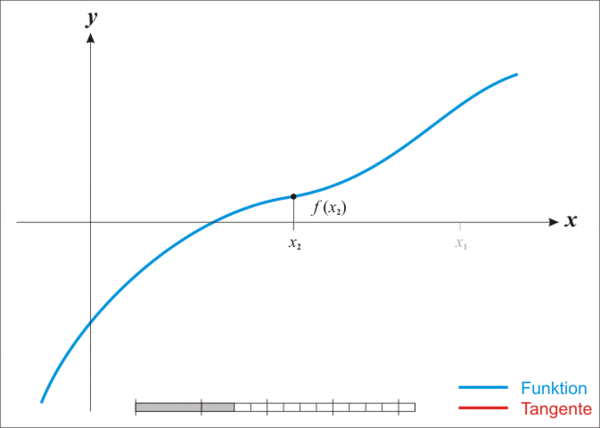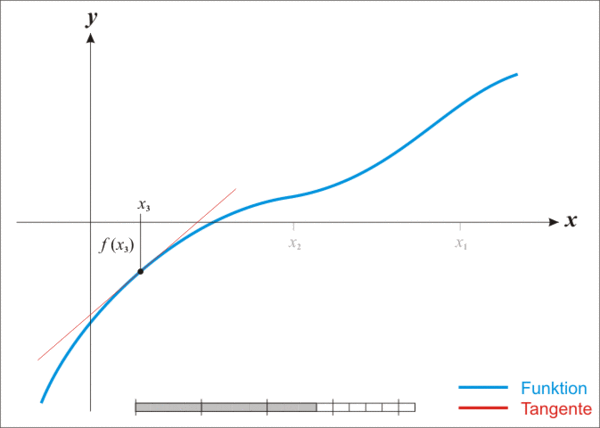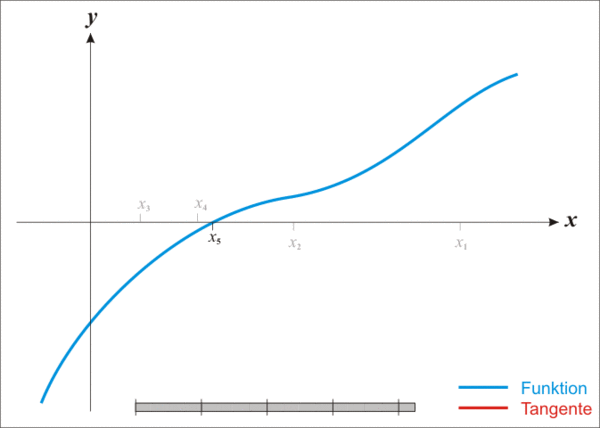
Historia[muokkaa | muokkaa wikitekstiä]
Newtonin menetelmän kuvasi Isaac Newton teoksissaan De analysi per aequationes numero terminorum infinitas (kirjoitettu 1669, julkaistu 1711) ja De metodis fluxionum et serierum infinitarum (kirjoitettu 1671, julkaistu nimellä Method of Fluxions 1736) Näissä teoksissa esitetty kuvaus eroaa kuitenkin nykyisestä, yllä esitetystä menetelmästä: Newton sovelsi menetelmää ainoastaan polynomeihin. Hän ei myöskään laskenut peräkkäisiä likiarvoja xn, vaan polynomijonoja päätyen vasta lopussa nollakohdan likiarvoon. Lisäksi Newton piti menetelmää puhtaasti algebrallisena eikä havainnut sen yhteyttä differentiaalilaskentaan. Isaac Newton luultavasti johti menetelmänsä samankaltaisesta mutta epätarkemmasta François Viète'n menetelmästä. Viète'n menetelmän perusta löytyy persialaisen matemaatikon Sharaf al-Din al-Tusin työstä.
Heron Aleksandrialainen käytti samankaltaista menetelmää kirjassa 1, luvussa 8 teoksessaan Metrica määrittääkseen luvun 720 neliöjuurta.
Newtonin menetelmän julkaisi ensimmäisenä John Wallis vuonna 1685 teoksessa A Treatise of Algebra both Historical and Practical. Joseph Raphson julkaisi yksinkertaistetun kuvauksen menetelmästä vuonna 1690 teoksessa Analysis aequationum universalis. Myös hän piti menetelmän puhtaasti algebrallisena rajoittaen sen käytön polynomeihin, mutta otti käyttöön peräkkäiset approksimaatiot likiarvoille xn. Ensimmäisenä Newtonin menetelmän kuvasi iteratiivisessa muodossa Thomas Simpson vuonna 1740.
Käytännön huomioita[muokkaa | muokkaa wikitekstiä]
Yleisesti ottaen Newtonin menetelmän virheen suuruus korottuu toiseen potenssiin joka askeleen jälkeen. Tämä tarkoittaa sitä, että tarkkojen desimaalien lukumäärä kaksinkertaistuu joka askeleella. Tämä ei kuitenkaan toimi joissakin tapauksissa. Ensinnäkin, Newtonin menetelmä vaatii derivaatan laskemista. Joissain tilanteissa sekanttimenetelmä on tehokkaampi. Toiseksi, jos alkuarvo on liian kaukana nollakohdasta, Newtonin menetelmä saattaa hajaantua. Kolmanneksi, jos etsitty nollakohta on moninkertainen, suppenemisnopeus on vain lineaarinen.
Vastaesimerkkejä[muokkaa | muokkaa wikitekstiä]
Näissä esimerkeissä etsitty juuri on nolla yksinkertaisuuden takia. Se voisi olla mikä tahansa muukin.
- Jos derivaatta ei ole jatkuva nollakohdassa, suppenemista ei välttämättä tapahdu.
Olkoon
ja
muualla.
Tällöin
ja
muualla.
Juuren missä tahansa ympäristössä derivaatta muuttaa merkkiään, kun x lähestyy nollaa oikealta (tai vasemmalta) samalla kun kaikille
Näin ollen Newtonin menetelmä ei suppene, vaikka funktio on kaikkialla derivoituva.
- Jos nollakohdassa ei ole toista derivaattaa, suppenemisnopeus ei ole verrannollinen toiseen potenssiin.
Olkoon
Tällöin
ja
paitsi kun , jossa se ei ole määritelty. Kun valitaan , , joka on noin 4/3 kertaa niin tarkka kuin . Tämä on vähemmän kuin kaksinkertainen tarkkuus.
Näin ollen Newtonin menetelmän suppenemisnopeus ei ole verrannollinen toiseen potenssiin, vaikka funktio onkin derivoituva kaikkialla.
- Jos funktion ensimmäinen derivaatta nollakohdassa on nolla, suppenemisnopeus ei ole verrannollinen toiseen potenssiin.
Olkoon
Tällöin ja . Näin ollen suppenemisnopeus ei ole verrannollinen toiseen potenssiin, vaikka funktion onkin äärettömän monta kertaa derivoituva kaikkialla.
Kirjallisuutta[muokkaa | muokkaa wikitekstiä]
- Kaleva, Osmo: Numeerinen analyysi. Opintomoniste 163. Tampere: TTKK, 1993. ISBN 951-721-941-5.
Aiheesta muualla[muokkaa | muokkaa wikitekstiä]
- Newton's method on Wolfram.com (englanniksi)
- Animations for Newton's method (englanniksi)
- Newton's method on the Mathcad Application Server (with animation) (englanniksi)
- Newton-Raphson Method Notes, PPT, Mathcad, Maple, Matlab, Mathematica at Holistic Numerical Methods Institute (englanniksi)
- Worked example (englanniksi)






















