Typistetty ikosaedri
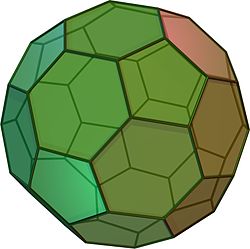
Typistetty ikosaedri eli katkaistu ikosaedri[1] on avaruusgeometriassa yksi kolmestatoista Arkhimedeen kappaleesta. Se on monitahokas, jolla on sivutahkoina 12 säännöllistä viisikulmiota ja 20 säännöllistä kuusikulmiota, ja sillä on 60 kärkeä ja 90 särmää.
Typistetty ikosaedri on Goldbergin monitahokas GPV(1,1) or {5+,3}1,1, jolla on viisi- ja kuusikulmaisia sivutahkoja.
Tavallisin nykyaikainen jalkapallo muistuttaa muodoltaan typistettyä ikosaedria[1], ja usein siinä kuusikulmaiset tahkot ovat valkoisia, viisikulmaiset mustia. Typistetty ikosaedri on usein rakenteen pohjana myös geodeettisissa kupoleissa, joiden suunnittelijana tuli tunnetuksi erityisesti Buckminster Fuller. Typistetyn ikosaedrin muotoinen on myös tunnetuin fullereenimolekyyli, buckminsterfullereeni C60.[1]
Typistettyä ikosaedriä käytetään myös solutransitiivisessa hyperbolisen avaruuden täyttävässä tessellaatiossa, kaksoistypistetyssä kertaluvun 5 dodekaedrisessa hunajakennossa.
Konstruktio
[muokkaa | muokkaa wikitekstiä]
Typistetty ikosaedri voidaan kostruoida lähtemällä ikosaedrista, jolla on 20 kolmiomaista tahkoa ja 12 kärkeä. Sen jokaisesta kärjestä leikataan pala pois siten, että jokaisen särmän kummastakin päästä leikataan kolmasosa pois. Täten ikosaedrin alkuperäisten kärkien ympärille syntyy 12 uutta viisikulmion muotoista tahkoa, ja ikosaedrin alkuperäisten kolmionmuotoisten tahkojen jäljelle jäävät osat muuttuvat kuusikulmion muotoisiksi. Näin ollen typistetyn ikosaedrin särmien pituus on vain kolmasosa alkuperäisen ikosaedrin särmien pituudesta.
Karteesiset koordinaatit
[muokkaa | muokkaa wikitekstiä]Kun typistetyn ikosaedrin keskipiste on origossa, sen kärkipisteiden karteesiset koordinaatit ovat:
- (0, ±1, ±3φ)
- (±1, ±(2 + φ), ±2φ)
- (±φ, ±2, ±φ3)
sekä näiden kaikki parilliset permutaatiot, missä on kultaisen leikkauksen suhdeluku. Sen ympäri piirretyn pallon säde on , ja särmien pituus on 2.
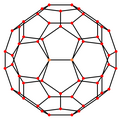
Ortogonaaliset projektiot
[muokkaa | muokkaa wikitekstiä]Typistetyllä ikosaedrilla on viisi erityistä ortogonaalista projektiota, joiden keskuksina ovat kärjet, kahdenlaiset särmät sekä kahdenlaiset sivutahkot: viisi- ja kuusikulmiot. Kaksi viimeksimainittua vastaavat Coxeterin tasoja A2 and H2.
| Keskuksena | Kärki | Särmä 5-6 |
Särmä 6-6 |
Tahko Viisikulmio |
Tahko Kuusikulmio |
|---|---|---|---|---|---|
| Kappale | 
|

|

| ||
| Särmien muodostama kuvio | 
|
|

|

|

|
| Projektiivinen symmetria |
[2] | [2] | [2] | [6] | [10] |
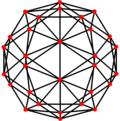
| Duaali | 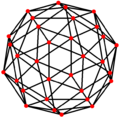
|
|

|

|

|
Ympyrän laatoitus
[muokkaa | muokkaa wikitekstiä]Typistetty ikosaedri voidaan kuvata myös ympyrän laatoituksena ja projisoida tasoille stereografisella projektiolla. Tämä projektio on konformikuvaus, toisin sanoen siinä kulmat säilyvät ennallaan, mutta pituudet ja pinta-alat eivät. Pallopinnan isoympyrät kuvautuvat tasolle ympyrän kaariksi.

|
 viisikulmio keskuksena |
 kuusikulmio keskuksena |
| Ortografinen projektio | Stereografiset projektiot | |
|---|---|---|
Mittasuhteet
[muokkaa | muokkaa wikitekstiä]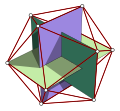
Jos typistetyn ikosaedrin särmän pituus on a, sen ympäri piirretyn eli sen kaikkia kärkiä koskettavan pallon säde on:
missä φ on kultaisen leikkauksen suhdeluku.
Tämä tulos saadaan helposti käyttämällä lähtökohtana yhtä niistä kolmesta toisiaan vastaan kohtisuorasta suorakulmiosta, jotka voidaan piirtää alkuperäisen ikosaedrin sisään, ennen kuin sen kärjet katkaistaan. Niiden janojen välinen kulma, jotka yhdistävät keskipisteen ja kaksi vierekkäistä kärkeä, voidaan laskea tämän konstruktion perusteella, ja se on noin 23,281446°.
Pinta-ala ja tilavuus
[muokkaa | muokkaa wikitekstiä]Kun typistetyn ikosaedrin särmän pituus on a, sen sivujen yhteenlaskettu pinta-ala on[2]
ja tilavuus
- .
Jos särmän pituutta käytetään pituusyksikkönä, viisikulmioiden yhteenlaskettu pinta-ala on suunnilleen 21 ja kuusikulmioiden 52 yksikköä, yhteensä vajaat 73 yksikköä.
Koska typistetty ikosaedri on kupera monitahokas, sen Eulerin karakteristika on
- .
Sovelluksia
[muokkaa | muokkaa wikitekstiä]


Tunnetuin typistettyä ikosaedria muistuttava esine on tavallinen jalkapallo.[1]. Siinä on 20 kuusikulmion ja 12 viisikulmion muotoista nahan tai muovin palasta ommeltu yhteen siten, että ne muodostavat typistetyn ikosaedrin, mutta kappaleen sisäisen paineen ja sen kimmoisuuden vaikutuksesta se on pullistunut tätä monitahokasta pallomaisemmaksi. Usein, esimerkiksi Adidas Telstar -pallossa siinä viisikulmion muotoiset tahkot ovat mustia, kuusikulmion muotoiset valkoisia. Tämän muotoisen jalkapallon suunnitteli tanskalainen jalkapalloilija Eigil Nilsson vuonna 1962[3], ja se otettiin virallisesti käyttöön jalkapallon maailmanmestaruuskilpailuissa 1970. Koska se muodoltaan muistuttaa geodeettista kupolia, sitä on toisinaan virheellisesti luultu Buckminster Fullerin suunnittelemaksi.[3] Vuodesta 2006 lähtien sen ovat pitkälti syrjäyttäneet uudenlaiset pallot. Myös käsipallossa käytetään typistetyn ikosaedrin muotoista palloa.
Geodeettinen kupoli on pääasiassa Buckminster Fullerin tunnetuksi tekemä rakennustyyppi, joka koostuu yhteen kiinnitetyistä monikulmion muotoisista levyistä ja tavallisimmin perustuu typistetyn ikosaedrin geometriaan. Tunnetuin tämän tyyppinen rakennelma on Fullerin suunnittelema, vuoden 1967 maailmannäyttelyyn rakennettu Biosphère Montréal[1]
Ikosaedrin muunnelmaa käytettiin pohjana, kun Pontiac Motor RIcision vuosina 1971–1976 valmisti rakenteeltaan hunajakennon kaltaisia pyöriä Trans Am- ja Grand Prix -automalleihin.
Tämän muotoisen yhdistelmän muodostivat myös linssit, joilla sytyttimen shokkiaalto saatiin keskitetyksi yhteen polttopisteeseen Gadget- ja Fat Man -atomipommeissa.[4]
Typistetyn ikosaedrin muotoinen on myös tunnetuin fullereenimolekyyli, buckminsterfullereeni (C60), joka on vuonna 1985 löydetty hiilen allotrooppinen muoto. Siinä hiiliatomit ovat sijoittuneet kappaleen kärkiin, ja lähimpien atomiytimien välinen etäisyys eli kappaleen särmän pituus on noin 0,71 nanometria. Kun särmän pituus jalkapallossa on 22 senttimetriä, on sen ja fullereenimolekyylin läpimittojen suhde noin 31,000,000:1.
Typistetty ikosaedri taiteessa
[muokkaa | muokkaa wikitekstiä]"Kiinteäsärmäinen" Leonardo da Vincin rakentama typistetty ikosaedri esiintyy eräässä kuvassa Luca Paciolin kirjassa De divina proportione.
Kuvia
[muokkaa | muokkaa wikitekstiä]-
Typistetyn ikosaedrin muotoinen radomi eli tutka-antennien suojarakennelma sääasemalla.
-
6061-T6-alumiinista valmistettu typistetty ikosaedri.
-
George W. Hartin puusta veistämä typistetty ikosaedri.
Typistettyyn ikosaedriin liittyviä monitahokkaita
[muokkaa | muokkaa wikitekstiä]Typistetyn ikosaedrin duaalikappale on pentakis-dodekaedri.[2]
Typistetty ikosaedri kuuluu uniformisiin ikosaedrisiin monitahokkaisiin, joita ovat seuraavat:
| Uniformiset ikosaedriset monitahokkaat | |||||||
|---|---|---|---|---|---|---|---|
| Symmetria: Ikosaedrinen symmetria [[5,3], (*532) | [5,3]+, (532) | ||||||

|

|

|

|

|

|

| |
| {5,3} | t{5,3} | r{5,3} | t{3,5} | {3,5} | rr{5,3} | tr{5,3} | sr{5,3} |
| Uniformisten monitahokkaiden duaalikappaleet | |||||||

|

|

|

|

|

| ||
| V5.5.5 | V3.10.10 | V3.5.3.5 | V5.6.6 | V3.3.3.3.3 | V3.4.5.4 | V4.6.10 | V3.3.3.3.5 |
On olemassa seuraavat uniformiset tähtimonitahokkaat, joiden uloimmat kärjet muodostavat typistetyn ikosaedrin:
|
Typistetyn ikosaedrin graafi
[muokkaa | muokkaa wikitekstiä]Matemaattisessa graafiteoriassa typistetyn ikosaedrin graafi on graafi, jonka muodostavat typistetyn ikosaedrin kärjet ja särmät. Sillä on 60 solmua ja 90 kaarta, ja se on kuutiollinen Arkhimedeen graafi.[5][6][7]
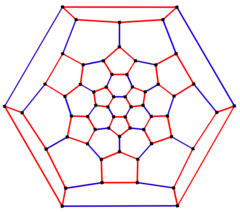 Kuusikulmainen Schlegelin diagrammi Icosahedron t01 H3.png|240px]] |
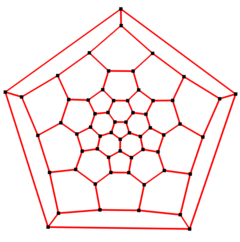 Viisikulmainen Schlegelin diagrammi |
Historia
[muokkaa | muokkaa wikitekstiä]Typistetyn ikosaedrin tunsi jo Arkhimedes, joka tutki kärkitransitiivisia monitahokkaita eli Arkhimedeen kappaleita. Hänen teoksensa ei kuitenkaan ole säilynyt. Myöhemmin Johannes Kepler löysi ne uudestaan ja kirjoitti niistä, myös typistetystä ikosaedristä.[8]
Saman monitahokkaan rakensi tai kuvasi myös Leonardo da Vinci.[9] Myös Albrecht Dürer teki mallin kappaleesta, jolla oli 12 viisikulmaista ja 20 kuusikulmaista tahkoa, joskaan asiasta säilyneet tiedot eivät ole aivan selviä.[10]
Lähteet
[muokkaa | muokkaa wikitekstiä]- Robert Williams: The Geometrical Foundation of Natural Structure: A Source Book of Design (luvut 3–9). Dover Publications, Inc., 1979. ISBN 0-486-23729-X.
- P. Cromwell: ”Archimedean Solids”, Polyhedra, s. 79–86. Cambridge, 1997. ISBN 0-521-55432-2.
Viitteet
[muokkaa | muokkaa wikitekstiä]- ↑ a b c d e Philip Ball: ”Kuinka osat sopivat yhteen: Hiilestä tehty jalkapallo”, Kemian eturintamassa, s. 61–62. Suomentanut Kimmo Pietiläinen. Terra Cognita, 1997. ISBN 952-5202-07-0.
- ↑ a b Truncated Icosahedron Wolfram MathWorld. Eric W. Weisstein. Viitattu 23.10.2018.
- ↑ a b Did Bucky Fuller really design a socker ball treehugger.com. 20.6.2014. Viitattu 24.10.2018.
- ↑ Richard Rhodes: Dark Sun: The Making og the Hydrogen Bomb, s. 195. Touchstone Books, 1996. ISBN 0-684-82414-0.
- ↑ Truncated Icosahedral Graph Wolfram MahtWorld. Eric W. Weissttein. Viitattu 23.10.2018.
- ↑ Godsil, C. and Royle, G. Algebraic Graph Theory New York: Springer-Verlag, p. 211, 2001
- ↑ Kostant, B. The Graph of the Truncated Icosahedron and the Last Letter of Galois. Notices Amer. Math. Soc. 42, 1995, pp. 959–968 PDF
- ↑ Archimedean Polyhedra George W. Hart. Viitattu 23.10.2018.
- ↑ C. Taliani, G. Ruani, R. Zamboni (toim.); L. Saffaro: ”Cosmoids, Fullerenes and continuous polygons”, Proceedings of the First Italian Workshop on Fullerenes: States and Perspectives, nide 2, s. 55. Singapore: {{{Julkaisija}}}, 1992. ISBN 9810210825.
- ↑ M. S. Dresselhaus, G. Dresselhaus, P. C. Eklund: Science of fullerenes and carbon nanotubes. San Diego: Academic Press, 1996. ISBN 012-221820-5.
Aiheesta muualla
[muokkaa | muokkaa wikitekstiä] Kuvia tai muita tiedostoja aiheesta Typistetty ikosaedri Wikimedia Commonsissa
Kuvia tai muita tiedostoja aiheesta Typistetty ikosaedri Wikimedia Commonsissa





















