Duaalikappale

Duaalikappale eli duaalimonitahokas on avaruusgeometriassa monitahokkaaseen liittyvä toinen monitahokas, jonka kärjet vastaavat alkuperäisen monitahokkaan tahkoja ja jonka kärkiä toisiinsa yhdistävät särmät vastaavat toisen tahkoja toisistaan erottavia särmiä.[1] Jokaisen monitahokkaan duaalikappaleen duaalikappale on yhdenmuotoinen alkuperäisen monitahokkaan kanssa.
Duaalisuudessa monitahokkaan symmetria säilyy. Niinpä monilla monitahokkaiden luokilla, jotka on määritelty symmetriaominaisuuksiensa avulla, on duaalikappaleet, jotka myös kuuluvat samaan symmetrialuokkaan. Niinpä esimerkiksi jokaisen säännöllisen Platonin kappaleen duaalikappale on toinen Platonin kappale, ja myös tähdenmuotoisten Keplerin–Poinsot’n kappaleen duaalikappale on toinen Keplerin–Poinsot’n kappale. Platonin kappaleista yksinkertaisin, säännöllinen tetraedri, on itse itsensä duaalikappale. Jos monitahokas on isogonaalinen eli sen kaikki kärjet ovat yhteneviä, sen duaali on isoedrinen, eli sen kaikki tahkot ovat yhteneviä. Jos monitahokas on isotoksinen eli sen kaikki särmät ovat yhtä pitkät, sen duaali on myös isotoksinen.
Duaalisuus liittyy läheisesti resiprositeettiin ja polaarisuuteen. Nämä ovat geometrisia muunnoksia, jotka kuperaan monitahokkaaseen sovellettuina antavat tulokseksi sen duaalikappaleen toisena kuperana monitahokkaana.
Duaalisuuden laadut[muokkaa | muokkaa wikitekstiä]

Kuvat Keplerin teoksesta Harmonices Mundi' (1619)
Duaalisuutta on monta tyyppiä. Yksinkertaisimpien monitahokkaiden kannalta tärkeimmät ovat polaarinen käänteisyys eli resiprositeetti ja topologinen eli abstrakti duaalisuus.
Polaarinen käänteisyys[muokkaa | muokkaa wikitekstiä]
Monitahokkaan duaalisuus määritellään usein polaarisen käänteisyyden avulla jonkin sopivasti valitun pallopinnan suhteen. Silloin jokaista kärkeä (napaa) vastaa sellainen sivutahko, että säde keskipisteestä kärkeen on kohtisuorassa tätä tahkoa vastaan ja että keskipisteestä tahkoihin mitattujen etäisyyksien tulo on sama kuin säteen neliö.[2][3] Koordinaateilla ilmoitettuna pisteessä
sijaitsevan särmän duaalinen taso pallon
suhteen on taso
- .
Duaalikappaleen kärjet ovat vastapäätä alkuperäisen kappaleen tahkoja, ja sen tahkot ovat vastapäätä alkuperäisen kappaleen kärkiä. Lisäksi alkuperäisen kappaleen mitkä tahansa kaksi vierekkäistä kärkeä määrittelevät särmän, ja duaalikappaleessa kutakin särmää vastaa näitä kärkiä vastaavien tahkojen välinen särmä. Alkuperäisen kappaleen ja duaalikappaleen toisiaan vastaavat särmät ovat aina kohtisuorassa toisiaan vastaan.
Jos on edellä kuvatun pallon säde ja ja sen keskipisteen etäisyydet jostakin alkuperäisen kappaleen kärjestä ja duaalikappaleen tahkon keskipisteestä, on
Symmetrisimmillä monitahokkailla on selvä keskipiste, ja tällöin pallo valitaan tavallisesti niin, että sen keskipiste on sama kuin monitahokkaan keskipiste. Näin tehdään esimerkiksi jäljempänä kuvautussa Dorman Luken konstruktiossa.
Monitahokkaalle voidaan kuitenkin muodostaa polaarisesti käänteinen duaalikappale minkä tahansa pallon suhteen, ja saadun duaalikappaleen muoto riippuu pallon sijainnista ja koosta. Kaikki duaalikappaleet, jotka muodostetaan sellaisten pallojen suhteen, joilla on yhteinen keskipiste, ovat kuitenkin keskenään yhdenmuotoiset. Jos kappaleella on useita symmetria-akseleita, ne leikkaavat toisensa aina samassa pisteessä, joka yleensä valitaan myös pallon keskipisteeksi. Ellei symmetria-akseleita ole tai niitä on vain yksi, valitaan tavallisimmin kappaleen ympäri tai sisään piirretty pallo taikka pallon, jonka tangentteja kaikki kappaleen särmät ovat.
Jos Euklidisessa avaruudessa jokin kappaleen särmistä tai tahkoista kulkee valitun pallon keskipisteen kautta tai keskipisteenä on jokin sen kärjistä, sitä duaalikappaleessa vastaava tahko tai särmä ulottuu äärettömän kauas tai tahkoa vastaava kärki on äärettömän kaukana. Euklidiseen avaruuteen ei kuulu äärettömän kaukaisia pisteitä, mutta sen projektiivinen vastine, jota sanotaan laajennetuksi euklidiseksi avaruudeksi, voidaan muodostaa lisäämällä siihen tarvittava äärettömän kaukainen taso. Jotkut teoreetikot pitäytyvät mieluummin euklidisessa avaruudessa ja päättelevät, että tällaisissa tapauksissa duaalikappaletta ei ole olemassa. Magnus Wenninger on kuitenkin keksinyt tavan, joilla voidaan tehdä malli tällaisten äärettömien duaalikappaleiden joistakin äärellisistä osista.[4]
Tällä duaalisuuden käsitteellä on läheinen yhteys projektiivisessa geometriassa esiintyvään duaalisuuden käsitteeseen, jossa tasot ja pisteet voidaan vaihtaa keskenään. Projektiivinen polaarisuus toimii riittävän hyvin kuperilla monitahokkailla. Mutta jos myös ei-kuperien kappaleiden, esimerkiksi tähtimonitahokkaiden duaalisuus yritetään täsmällisesti määritellä projektiivisen polaarisuuden avulla, ilmenee monia ongelmia.[5][6] Wenninger on myös tutkinut tapoja, joilla nämä äärettömät duaalikappaleet voidaan muodostaa. Ei-kuperien monitahokkaiden geometriseen duaalisuuteen liittyvien määritelmällisten kysymysten vuoksi Branko Grünbaum on esittänyt, että jokaiseen ei-kuperan monitahokkaan asianmukaiseen määritelmään pitäisi kuulua myös selvitys siitä, miten sen duaalikappale muodostetaan.[7]
Kanoniset duaalit[muokkaa | muokkaa wikitekstiä]

Jokaista kuperaa monitahokasta vastaa kanoninen muoto, jolla on midsfääri eli intersfääri, toisin sanoen pallo, jonka tangentteja tämän kanonisen muodon kaikki särmät ovat. Tämä kanoninen muoto on sikäli yksikäsitteinen, että kaikki samaa monitahokasta vastaavat kanoniset muodot kappaleina ovat yhtenevät.
Jos tälle kanoniselle monitahokkaalle muodostetaan polaarisesti käänteinen duaalikappale, sen särmät ovat saman pallon tangentteja ja sivuavat sitä samoissa pisteissä, joten se on myös kanoninen. Sitä sanotaan kanoniseksi duaaliksi, ja nämä kaksi kappaletta yhdessä muodostavat kanonisen duaaliparin.[8]
Topologinen duaalisuus[muokkaa | muokkaa wikitekstiä]
Siinäkin tapauksessa, että monitahokkaista ei voida muodostaa toistaan edellä kuvatulla polaarisella käänteisyydellä, niitä voidaan sanoa toistensa duaalikappaleiksi, mikäli toisen särmät vastaavat toisen tahkoja ja kummankin särmät toisiaan siten, että samassa kärjessä kohtaavia särmiä vastaavat duaalikappaleessa samaa tahkoa rajoittavat särmät ja päinvastoin. Tällaisia monitahokaspareja sanotaan toistensa topologisiksi eli abstrakteiksi duaaleiksi.
Kuperan monitahokkaan kärjet ja särmät muodostavat graafin, joka voidaan upottaa topologiselle pallopinnalle, joka on homeomorfinen monitahokkaan pinnan kanssa.
Sama graafi voidaan projisoida tasolle niin, että siitä muodostuu Schlegelin diagrammi. Monitahokkaan duaalikappaleesta samalla tavalla muodostettu graafi on tämän graafin duaaligraafi. Yleensäkin jokaisella monitahokkaalla, jonka tahkot muodostavat suljetun pinnan, sen kärjet ja räsmät muodostavat graafin, joka voidaan upottaa tälle pinnalle, ja tämän monitahokkaan abstraktin duaalikappaleen kärjet ja särmät muodostavat sen duaaligraafin.
Abstrakti monitahokas on eräänlainen osittain järjestetty joukko, jonka alkiot vastaavat monitahokkaan kärkiä, särmiä ja tahkoja ja jonka alkioiden väliset yhteydet vastaavat monitahokkaan tahkojen tai särmien välisiä yhteyksiä. Jokaisella tällaisella osittain järjestetyllä joukolla on duaalijoukko, joka myös on osittain järjestetty ja joka saadaan kääntämällä kaikki järjestysrelaatiot. Jos tämä joukko visualisoidaan Hassen diagrammilla, sen duaalijoukko voidaan visualisoida yksinkertaisesti kääntämällä Hassen diagrammi ylösalaisin.
Jokainen geometrinen monitahokas vastaa tällä tavoin jotakin abstraktia monitahokasta, ja sillä on abstrakti duaalimonitahokas. Joidenkin ei-kuperien geometristen monitahokkaiden tapauksessa tätä duaalimonitahokasta ei kuitenkaan voida toteuttaa geometrisesti.
Dorman Luken konstruktio[muokkaa | muokkaa wikitekstiä]
Monitahokas on uniforminen, jos sen tahkot ovat säännöllisiä monikulmioita ja se voidaan kuvata yhtenevyyskuvauksella itselleen niin, että mikä tahansa sen kärjistä voidaan tällaisella kuvauksella kuvata mille tahansa toiselle kärjelle. Tällaisen monikulmion duaalikappaleen tahko saadaan alkuperäisen monitahokkaan kärkikuviosta Dorman Luken konstruktiolla.[9][10]
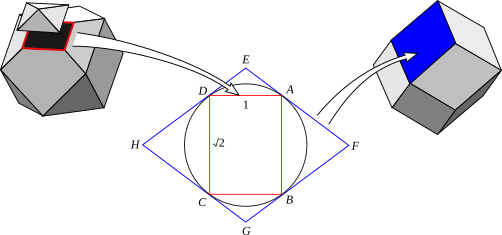
Esimerkiksi alla oleva kuva osoittaa, miten kuboktaedrin kärkikuviosta (punainen) saadaan johdetuksi sen duaalikappaleen, rombidodekaedrin tahko.
Ennen kuin konstruktio voidaan aloittaa, kärkikuvio ABCD saadaan jakamalla kyseiseen kärkeen johtavat särmät kukin keskipisteestään kahtia.
Dorman Luken konstruktio jatkuu täten seuraavasti:
- Piirretään kärkikuvio ABCD
- Piirretään nelikulmion ABCD ympäri piirretty ympyrä (joka kulkee jokaisen pisteen A, B, C ja D kautta)Draw the circumcircle (tangent to every corner A, B, C and D).
- Piirretään tälle ympyrälle pisteiden A, B, C ja D kautta kulkevat tangentit
- Merkitään näiden tangenttien leikkauspisteet: E, F, G, H
- The Nelikulmio EFGH on duaalikappaleen tahko.
Tässä tapauksessa kärkikuvio valittiin niin, että sen ympäri piirretty ympyrä on kuboktaedrin sisään piirretyllä pallopinnalla, josta tulee myös rombidodekaedrin sisään piirretty pallo.
Dorman Luken konstruktio on mahdollista vain sellaisille monitahokkaille, joiden sisään piirretty pallo ja kärkikuvio ovat syklisiä. Sellaisia ovat muun muassa kaikki uniformiset monitahokkaat.
Esimerkkejä[muokkaa | muokkaa wikitekstiä]
Viidestä Platonin kappaleesta tetraedrin duaalikappale on toinen tetraedri. Kuutio ja säännöllinen oktaedri ovat toistensa duaalikappaleita, samoin säännöllinen dodekaedri ja ikosaedri.[11]
Itseduaaliset monitahokkaat[muokkaa | muokkaa wikitekstiä]
Monitahokas on topologisesti itseduaalinen, jos sen duaalikappaleen kärjet, särmät ja tahkot liittyvät toisiinsa samalla tavalla. Tällöin alkuperäisellä monitahokkaalla ja sen duaalikappaleella on sama Hassen diagrammi.
Monitahokas on geometrisesti itseduaalinen, jos se on topologisesti itseduaalinen ja jos lisäksi sen polaarisesti käänteinen duaalikappale jonkin pisteen, tavallisesti kappaleen keskipisteen suhteen on alkuperäisen kappaleen kanssa yhdenmuotoinen. Esimerkiksi säännöllisen tetraedrin duaalikappale on toinen säännöllinen tetraedri, alkuperäisen kappaleen peilikuva sen painopisteen suhteen.
Erilaisia geometrisesti itseduaalisia monitahokkaita on äärettömän monta. Jokainen topologisesti itseduaalinen kupera monitahokas on homeomorfinen jonkin geometrisesti itseduaalisen monitahokkaan, kanonisen monitahokkaan kanssa.
Yksinkertaisimman ryhmän geometrisesti itseduaalisia monitahokkaita muodostavat kanoniset n-sivuiset pyramidit[12], missä n on kokonaisluku ja vähintään 3. Toisen äärettömän ryhmän muodostavat jatketut pyramidit, jotka voidaan käsittää pyramidin ja yhtä monisivuisen prisman yhdistelmiksi. Katkaistut pyramidit ovat myös geometrisesti itseduaalisia. Lisäksi on vielä koko joukko muita: esimerkiksi on kuusi erilaista 7-kärkistä ja kuusitoista 8-kärkistä geometrisesti itseduaalista monitahokasta.[13]
On olemassa myös ei-kuperia itseduaalisia monitahokkaita. Esimerkiksi Brückner kuvasi vuonna 1900 erään itseduaalisen monitahokkaan, jolla on 20 kuusikulmion muotoista sivua.[14][15][16]
 3 |
 4 |
 5 |
 6 |
 3 |
 4 |
 5 |
 3 |
 4 |
 5 |
 6 |
 7 |
Itseduaaliset yhdistetyt monitahokkaat[muokkaa | muokkaa wikitekstiä]
Mistä tahansa monitahokkaasta ja sen duaalikappaleesta yhdistämällä saatu kappale on selvästi itseduaalinen.
Jos monitahokas on itseduaalinen, sen ja sen duaalikappaleen yhdistelmä koostuu kahdesta yhtenevästä monitahokkaasta. Tällaisesta ainoa säännöllinen kappale on kahden tetraedrin yhdistelmä, joka tunnetaan nimellä Stella octangula.
Duaaliset polytoopit ja tessellaatiot[muokkaa | muokkaa wikitekstiä]
Duaalisuus voidaan yleistää mihin tahansa n-ulotteiseen avaruuteen, jolloin puhutaan duaalisista polytoopeista. Kahdessa ulottuvuudessa niitä sanotaan duaalisiksi monikulmioiksi.
Kahdessa ulottuvuudessa jokainen monikulmio on topologisesti itseduaalinen, sillä jokaisella monikulmiolla on yhtä monta sivua kuin kärkeä, ja sivut ja kärjet vastaavat duaalissa toisiaan. Useimmat monikulmiot eivät kuitenkaan ole geometrisesti itseduaalisia. Säännölliset monikulmiot kuitenkin ovat geometrisesti itseduaalisia sisään piirretyn ympyränsä suhteen: kaikki kulmat ovat yhtä suuria, samoin kaikki sivut, ja duaalisuudessa kulmat ja sivut vastaavat toisiaan.
Duaalisuudessa toisen polytoopin kärjet vastaavat toisen (n − 1) -ulotteisia elementtejä, ja ne j pistettä, jotka määrittävät (j − 1)-ulotteisen elementin, vastaavat j hypertasoa, jotka leikkaavat toisensa muodostaen (n − j) -ulotteisen elementin. Samaan tapaan voidaan määrittää n-ulotteinen tessellaatio.
Yleisesti polytoopin duaalin sivut vastaavat alkuperäisen polytoopin kärkikuviota. Säännöllisten ja uniformisten polytooppien polaaristen käänteispolytooppien sivut ovat alkuperäisen polytoopin kärkikuvion polaarisia käänteiskuvioita. Esimerkiksi neljässä ulottuvuudessa 600-solun kärkikuvio on säännöllinen ikosaedri; 600-solun duaalikappale on 120-solu, jonka sivut ovat dodekaedreja, ja dodekaedri on ikosaedrin duaalikappale.
Itseduaaliset polytoopit ja tessellaatiot[muokkaa | muokkaa wikitekstiä]


Ensisijaisen luokan itseduaalisia polytooppeja muodostavat säännölliset polytoopit, joilla on palindrominen Schläflin symboli. Kaikki säännölliset monikulmiot, {a}, ovat itseduaalisia, samoin muotoa {a,a} olevat monitahokkaat, muotoa {a,b,a} olevat 4-polytoopit, muotoa {a,b,b,a} olevat 4-polytoopit ja niin edelleen.
Itseduaaliset säännölliset polytoopit ovat:
- Kahdessa ulottuvuudessa kaikki säännölliset monikulmiot, {a}
- Kolmessa ulottuvuudessa säännöllinen tetraedri: {3,3}
- Yleisesti kaikki säännölliset n-simpleksit, {3,3,...,3}
- Neljässä ulottuvuudessa:
- säännöllinen 24-solu neljässä ulottuvuudessa
- suuri 120-solu {5,5/2,5} ja suuri stellatoitu 120-solu {5/2,5,5/2}
Itseduaalisia äärettömiä säännöllisiä euklidisia tessellaatioita ovat:
- Apeirogoni: {∞}
- Neliölaatoitus: {4,4}
- Kuutiollinen tessellaatio: {4,3,4}
- Yleisesti kaikki säännölliset n-ulotteiset euklidiset hyperkuutiolliset tessellaatiot: {4,3,...,3,4}.
Itseduaalisia äärettömiä säännöllisiä hyperbolisia tessellaatioita ovat:
- Kompkatit hyperboliset laatoitukset: {5,5}, {6,6}, ... {p,p}.
- Parakompakti hyperbolinen laatoitus: {∞,∞}
- Kompaktit hyperboliset tessellaatiot: {3,5,3}, {5,3,5} ja {5,3,3,5}
- Parakompaktit hyperboliset tessellaatiot: {3,6,3}, {6,3,6}, {4,4,4} ja {3,3,4,3,3}
Lähteet[muokkaa | muokkaa wikitekstiä]
- ↑ Magnus Wenninger: ”Basic notions about stellation and duality”, Dual Models. Cambridge University Press, 1983. ISBN 0-521-54325-8.
- ↑ H. Mardyn Cundy, A. P. Rollett: ”Duality”, Mathematical Models (2nd ed.),, s. 78–79. Oxford: Clarendon Press, 1961.
- ↑ Magnus Wenninger: Dula Models, s. 3–5. Cambridge University Press, 1983. ISBN 0-521-54325-8.
- ↑ Magnus Wenninger: Dual Models. Cambridge University Press, 1983. ISBN 0-521-54325-8.
- ↑ Marjorie Senechal (toim); Branko Grünbaum, G. C. Shephard: ”Duality of polyhedra”, Exploring polyhedra in nature, art, and the geometrical imagination, s. 211–216. Springer, 2013. ISBN 978-0-387-92713-8. doi:10.1007/978-0-387-92714-5_15.
- ↑ Duality of polyhedra. International Journal of Mathematical Education in Science and Technology, 2005, 36. vsk, nro 6, s. 617–642. doi:10.1080/00207390500064049.
- ↑ Boris Aronov, Saugata Basu, János Pach, Micha Sharir (toim.); Branko Grünbaum: ”Are your polyhedra the same as my polyhedra?”, Discrete and Computational Geometry: The Goodman–Pollack Festschrift, s. 461–488. Springer, 2005. doi:10.1007/978-3-642-55566-4_21.
- ↑ Graphs of polyhedra; polyhedra as graphs (Theorem 3.1). Discrete Mathematics, 2007, 307. vsk, nro 3–5, s. 449. doi:10.1016/j.disc.2005.09.037.
- ↑ H. Martyn Cundy, A. P. Rollett: Mathematical Models, s. 117. Oxford: Clarendon Press, 1961.
- ↑ Magnus Wenninger: Dual Models, s. 30. Cambridge University Press, 1983. ISBN ISBN 0-521-54325-8.
- ↑ Dual Polyhedron Wolfram MathWorld. Eric W. Weisstein. Viitattu 25.6.2018.
- ↑ Self-Dual Polyhedron Wolfram MathWorld. Eric W. Weisstein. Viitattu 25.6.2018.
- ↑ Symmetries of Canonical Sel-dual Polyhedra dmccooey.com. Viitattu 25.6.2018.
- ↑ Regular Polyhedra of Index Two",. Beiträge zur Algebra und Geometrie / Contributions to Algebra and Geometry, Huhtikuu 2011, 52. vsk, nro 1, s. 133–161.
- ↑ Faceting the Dodecahedron. (Kuva 3c ja siihen liittyvä teksti) Acta Crystallographica, Heinäkuu 1974, nro A 30, osa 4.
- ↑ M. Brückner: Vielecke und Vielflache: Theorie und Geschichte. Teubner: Teubner, 1900.