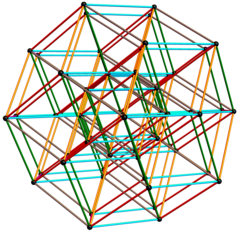
Rombinen triakontaedri



Rombinen triakontaedri, jota toisinaan sanotaan lyhyesti triakontaedriksi, on geometriassa kupera monitahokas, jonka tahkoina on 30 neljäkästä. Sillä on 60 särmää ja kahdenlaisia kärkiä yhteensä 32. Se kuuluu Catalanin kappaleiksi ja on ikosidodekaedrin duaalikappale.[1] Se on myös zonoedri.[1]
Rombisen triakontaedrin jokaisen tahkon pidemmän ja lyhemmän lävistäjän suhde on tarkalleen kultainen leikkaus, φ, minkä vuoksi tahkojen terävät kulmat ovat suuruudeltaan 2 tan−1(1φ) = tan−1(2), eli suunnilleen 63.43°. Tällaista neljäkästä sanotaan kultaiseksi neljäkkääksi.
Koska rombinen triakontaedri on Arkhimedeen kappaleen duaalikappale, se on tahkotransitiivinen. Tämä merkitsee, että jos kappaleesta valitaan mitkä tahansa kaksi tahkoa A tai B, on olemassa sellainen kappaleen yhtenevyyskuvaus, jossa kuva vie avaruudessa saman alueen kuin alkuperäinen kappale ja jossa tahko A kuvautuu tahkolle B.
Rombinen triakontaedri on myös särmätransitiivinen. Erilaisia särmätransitiivisia monitahokkaita on vain yhdeksän; muut ovat viisi Platonin kappaletta sekä kuboktaedri, ikosidodekaedri ja rombidodekaedri.
Rombisella triakontaedrilla on 12 sellaista kärkeä, joissa kohtaa toisensa viisi tahkoa. Lopuissa 20 kärjessä kohtaa toisensa kolme tahkoa kussakin.
Rombinen triakontaedri on myös siitä erikoinen, että osa sen kärjistä voidaan yhdistää toisiinsa kappaleen avaruuslävistäjillä niin, että saadaan neljä Platonin kappaleista. Tällä tavoin se sisältää neljä tetraedria, viisi kuutiota, yhden ikosaedrin ja yhden dodekaedrin. Sen tahkojen keskipisteistä voidaan muodostaa viisi oktaedria.
Kappale voidaan muodostaa typistetystä oktaedrista jakamalla sen kuusikulmaiset sivut kolmeksi neljäkkääksi:

Mittasuhteet[muokkaa | muokkaa wikitekstiä]
Jos rombisen triakontaedrin särmän pituus on a, sen tahkojen yhteenlaskettu pinta-ala (S), tilavuus (V), sisään piirretyn pallon säde (ri) sekä sellaisen pallon säde, joka kulkee jokaisen särmän keskipisteen kautta (rm), ovat:
missä φ on kultaisen leikkauksen suhdeluku.
Kappaleen sisään piirretty pallo sivuaa sen jokaista tahkoa sen keskipisteessä. Rombisen ikosaedrin tahkojen lyhyet lävistäjät muodostavat säännöllisen dodekaedrin, pitkät särmät säännöllisen ikosaedrin.[1]
Jako osiin[muokkaa | muokkaa wikitekstiä]
Rombinen triakontaedri voidaan jakaa 20 kultaiseen romboedriin, joista 10 on terävä- ja 10 tylppäkulmaisia.[2][3]
| 10 | 10 |
|---|---|
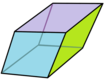 Teräväkulmainen kultainen romboedri |
 Tylppäkulmainen kultainen romboedri |
Ortogonaaliset projektiot[muokkaa | muokkaa wikitekstiä]
Rombisella triakontaedrillä on neljänlaisia symmetristä ortogonaalista projektiota, joista kahdella on keskuksena kappaleen kärjet, yhdellä särmän keskipiste ja yhdellä tahkon keskipiste. Projektioon "10" sisältyvät "paksu" ja "ohut" neljäkäs, joiden kopioilla taso voidaan täyttää niin, että muodostuu Penrosen laatoiksi nimitetty epäjaksollinen tessellaatio.
| Projektiivinen symmetria |
[2] | [2] | [6] | [10] |
|---|---|---|---|---|
| Kuva | 
|

|

|

|
| Duaalin kuva |

|

|

|

|
Stellaatiot[muokkaa | muokkaa wikitekstiä]

Rombisella triakontaedrilla on kaikkiaan 358 833 097 stellaatiota, joista kuitenkin vain 227 on täysin tuettuja (engl. fully supported). Stellaatiossa tahkon alapuoli saattaa ulkopuolelta katsottuna näyttää roikkuvalta ulokkeelta. Täysin tuetussa stellaatioissa tällaisia ulokkeita ei ole, vaan jokainen jokainen tahko on joltakin puolelta katsottuna kokonaisuudessaan nähtävissä.[4][5]
Triakontaedri ja muut monitahokkaat[muokkaa | muokkaa wikitekstiä]
| Uniformiset ikosaedriset monitahokkaat | |||||||
|---|---|---|---|---|---|---|---|
| Symmetria: [5,3], (*532) | [5,3]+, (532) | ||||||

|

|

|

|

|

|

|

|
| {5,3} | t{5,3} | r{5,3} | t{3,5} | {3,5} | rr{5,3} | tr{5,3} | sr{5,3} |
| Uniformisten monitahokkaiden duaalit | |||||||

|

|

|

|

|

| ||
| V5.5.5 | V3.10.10 | V3.5.3.5 | V5.6.6 | V3.3.3.3.3 | V3.4.5.4 | V4.6.10 | V3.3.3.3.5 |
Tämä monitahokas kuuluu rombisten monitahokkaiden ja laatoitusten sarjaan, jolla on Coxeterin ryhmän [n,3] mukainen symmetria. Kuutiota voidaan pitää rombisena heksaedrina, jonka neljäkkäät ovat samalla myös suorakulmioita.
| Duaalisten kvasireguaaristen laatoitusten symmetriamuunnokset: V(3.n)2 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| *n32 | Sfäärinen | Euklidinen | Hyperbolinen | ||||||||
| *332 | *432 | *532 | *632 | *732 | *832... | *∞32 | |||||
| Laatoitus | 
|

|

|

|

|

|

| ||||
| Konfig. | V(3.3)2 | V(3.4)2 | V(3.5)2 | V(3.6)2 | V(3.7)2 | V(3.8)2 | V(3.∞)2 | ||||
}}
-
Rombinen triakontaedri pallopinnalla
-
Rokbinen triakontaedri, jonka sisään on piirretty tetraedri (punainen) ja kuutio (sininen).
(Tästä klikkaamalla saa näkyviin pyörivän mallin) -
Rombinen triakontaedri, jonka sisään on piirretty dodekaedri (sininen) ja ikosaedri (violetti).
(Tästä klikkaamalla saa näkyviin pyörivän mallin) -
Täysin katkaistu rombinen triakontaedri
6-kuutio[muokkaa | muokkaa wikitekstiä]
Rombinen triakontaedri muodostaa 32-kärkisen kuperan peitteen yhdelle 6-kuution kolmiulotteisista projektioista.
Käyttö[muokkaa | muokkaa wikitekstiä]

.

Tanskalainen muotoilija Holger Strøm on käyttänyt rombista triakontaedria pohjana muotoillessaan koottavan IQ-light -nimisen lampun. Lyhenne IQ tulee sanoista Interlocking quadrilaterals, toisiinsa tarttuneet nelikulmiot.[6]
Puuseppä Jane Kostick rakentaa rombisen triakontaedrin muotoisia laatikoita.[7] Niiden rakenne perustuu vähemmän ilmeiseen yhteyteen rombisen triakontaedrin ja kuution välillä.
Roger von Oechin "Ball of Whacks" on rombisen triakontaedrin muotoinen.
Joissakin roolipeleissä käytetään rombisen triakontaedrin muotoista 30-sivuista d30-noppaa.
Lähteet[muokkaa | muokkaa wikitekstiä]
- Robert William: The Geometrical Foundation of Natural Structure: A Source Book of Design. (luvut 3–9). Dover Publications, Inc, 1979. ISBN 0-486-23729-X.
- Magnus Wenninger: ”Rhombic triacontahedron”, Dual Models, s. 22. Cambridge University Press, 1983. doi:10.1017/CBO9780511569371.
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass: ”Naming the Archimedean and Catalan polyhedra and tilings, Rhombic triacontahedron”, The Symmetry of Things, s. 285. , 2008. ISBN 978-1-56881-220-5. Teoksen verkkoversio.
Viitteet[muokkaa | muokkaa wikitekstiä]
- ↑ a b c Rhombic Triacontahedron Wolfram MathWorld. Erik W. Weisstein. Viitattu 19.9.2019.
- ↑ Golden Rhombohedra cutoutfoldup.com. Viitattu 20.9.2019.
- ↑ Dissection of the rhombic triacontahedron georgehart.com. Viitattu 20.9.2019.
- ↑ G. S. Pawley: The 227 triacontahedra. Geometriae Dedicata, 1975, nro 2–4, s. 221–232. Kluwer Academic Publishers. ISSN 1572-9168. doi:10.1007/BF00148756.
- ↑ P. W. Messer: Stellations of the Rhombic Triacontahedron and Beyond. Structural Topology, 1995, s. 25–46.
- ↑ IQlight konceptet Halo Design. Arkistoitu 23.9.2019. Viitattu 23.9.2019. (tanskaksi)
- ↑ triacontahedron box - KO Sticks LLC kosticks.com. Viitattu 23.9.2019.
Aiheesta muualla[muokkaa | muokkaa wikitekstiä]
- Rhombic Triacontahedron polyhedra.org. Arkistoitu 1.7.2007. Viitattu 23.9.2019.
- Stellations of rhombic triacontahedron john Cranmer, Peter W. Messer.
- Rhombic Triacontahedron (Rombisen triakontaedrin muotoisen origamin valmistusohje) instructables.com.