Bohrin atomimalli
| Tähän artikkeliin tai osioon ei ole merkitty lähteitä, joten tiedot kannattaa tarkistaa muista tietolähteistä. Voit auttaa Wikipediaa lisäämällä artikkeliin tarkistettavissa olevia lähteitä ja merkitsemällä ne ohjeen mukaan. |
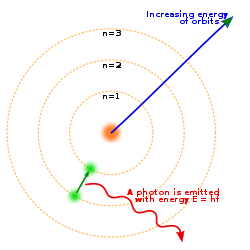
Bohrin atomimalli on ensimmäinen semikvanttimekanistinen fysikaalinen atomimalli, joka kuvaa atomin pieneksi positiivisesti varautuneeksi ytimeksi, jota elektronit kiertävät eritasoisilla radoilla, kuten planeetat kiertävät Aurinkoa ja kuut planeettoja. Vaikka Bohrin malli osoittautui myöhemmin puutteelliseksi, onnistui se kuitenkin selittämään paljon ilmiöitä. Malli on myös verrattain yksinkertainen, minkä takia Bohrin atomimallia opetetaan vielä nykyäänkin yleisesti yläkouluissa sekä lukioissa.
Taustaa[muokkaa | muokkaa wikitekstiä]
1900-luvun alkupuolella Ernest Rutherford havaitsi pommittamalla ohutta kultakalvoa heliumytimillä (eli alfahiukkasilla), että atomit koostuivat pienestä ja tiiviistä positiivisesti varautuneesta ytimestä, jota ympäröivät negatiivisesti varautuneet elektronit. Useimmat alfahiukkaset läpäisivät kalvon vaivattomasti, johtaen tulkintaan atomista, joka on enimmäkseen tyhjää tilaa. Kuitenkin jotkut alfahiukkaset taittuivat takaisin kalvosta hyvinkin suurilla kulmilla; kokeen datan perusteella atomiydin olisi korkeintaan m. Rutherfordin omin sanoin: "It was quite the most remarkable event that has ever happened to me in my life. It was almost as if you fire a fifteen-inch shell at a piece of tissue paper and it came back and hit you". Oli kuitenkin epäselvää, mikseivät negatiiviset elektronit pudonneet positiiviseen ytimeen.
Lisäksi atomien absorptio- ja emissiospektreistä oli jo kauan aikaisemmin huomattu, että jokaisella alkuaineella on sille ominainen karakteristinen spektri eli ne lähettävät valoa vain tietyillä aallonpituuksilla. Esimerkiksi natriumlanka lähettää vain tietyillä spesifisillä aallonpituuksilla valoa, kun atomeille annetaan energiaa esimerkiksi sähköpurkauksen avulla. Klassinen fysiikka ei pystynyt selittämään ilmiötä, mikä ei kuitenkaan ollut estänyt käyttämästä sitä hyväksi alkuaineiden tunnistamisessa.
Bohrin postulaatit[muokkaa | muokkaa wikitekstiä]
Niels Bohr ehdotti atomimallia, jossa elektronit kiertävät ellipsiradoilla kompaktia ydintä. Malli siis pitää elektroneita täysinä hiukkasina, vaikka nykyään tiedämme, että elektronit noudattavat aaltohiukkasdualismia. Atomeista yksinkertaisin on vetyatomi, joka koostuu protonista ja sitä kiertävästä elektronista. Koska ydin on positiivisesti ja elektroni negatiivisesti varautunut, vetävät ne toisiaan puoleensa Coulombin voiman ansiosta, samalla tavalla kuin Aurinko vetää Maata (ja Maa Aurinkoa) puoleensa painovoiman vaikutuksesta. Ensimmäinen ongelma tällä mallilla on, että jos elektroni kiertää ydintä kiertoradalla, pitäisi sen lähettää sähkömagneettista säteilyä, koska se on kiihtyvässä liikkeessä ja kiihtyvät varaukset lähettävät sähkömagneettista säteilyä. Tämän säteilyn taajuuden pitäisi olla sama kuin sen kiertoajan käänteisarvo. Siitä kuitenkin seuraisi, että elektroni menettäisi energiaa ja tämän vuoksi sen kiertosäde pieneneisi, kunnes se olisi ytimessä noin sekunnin kuluttua. Bohrin atomimalli (1913) kuitenkin onnistui ratkaisemaan tämän ongelman tekemällä lisäoletuksia, postulaatteja, jotka kuitenkin merkitsivät selvää poikkeamista klassisesta fysiikasta.
Bohrin postulaatit:
- Elektronit kiertävät ydintä kiertoradoilla
- Elektronin pyörimismäärä on kvantittunut: , missä n = 1, 2, 3, ...
- Klassiset mekaniikan lait eivät päde, kun elektronit virittyvät tai purkautuvat sallitulta kiertoradalta toiselle.
- Elektroni ei lähetä säteilyä ollessaan tietyllä kiertoradalla vaan ainoastaan siirtyessään ylemmältä kiertoradalta alemmalle.
- Kun elektroni hyppää kiertoradalta toiselle, energiaero joko poistuu tai saapuu yksittäisenä valokvanttina eli fotonina, jonka taajuus riippuu suoraan kyseisten kiertoratojen välisestä energiaerosta. Kvantin energian ja säteilyn taajuuden välillä vallitsee sama yhteys, jonka Max Planck oli jo vuonna 1900 esittänyt mustan kappaleen säteilylle: , missä f on fotonin taajuus, E on energiaero ja h on yleinen luonnonvakio, joka tunnetaan Planckin vakiona.
Kun määritellään , voimme kirjoittaa , missä ω on fotonin kulmataajuus.
Postulaattien seuraukset[muokkaa | muokkaa wikitekstiä]
Koska Bohrin malli toimii täydellisesti vain vetyatomille, seuraavassa on implisiittisesti kyse vetyatomista. Jos kyseessä on jonkin muun alkuaineen yksielektroninen ioni, on kaavoissa e2 korvattava lausekkeella Ze2, missä Z on alkuaineen järjestysluku ja Ze ytimen varaus.
Postulaatti 2 on koko mallin ydin. Siitä seuraa, että elektronin säde ja energia ovat kvantittuneet, eli ne voivat saada vain tiettyjä arvoja. Toisinaan näiden kvantittumiset ovat virheellisesti oletettu mallin postulaateiksi, vaikka todellisuudessa ne ovat vain seurausta postulaatista 2. Seuraavassa oletamme, että ydin on massaltaan suuri verrattuna elektroniin, jolloin kiertorata on ympyrä, jonka keskipiste on ytimessä.
Pyörimismäärälle (1), missä = elektronin kiertoradan säde tietylle n, m = elektronin massa sekä v = elektronin tangentiaalinen nopeus ja n = 1, 2, 3, ...
Coulombin voima toimii sentripetaalisena voimana, joten: (2)
Eliminoimalla v (1):stä ja (2):sta saadaan:
- (3),
eli säde on kvantittunut. Määritellään vakio , joka tunnetaan Bohrin säteenä, jolloin (4).
Elektronin energia ja spektrit[muokkaa | muokkaa wikitekstiä]
Koska elektronin kokonaisenergialle pätee:
- ,
(2):sta eliminoimalla v saamme
- .
Sijoittamalla tähän (3) saamme
- eV (5).
Kaava (5) ennustaa täydellisesti vedyn emissiospektrin. Sen mukaan vetyatomi voi lähettää vain sellaisia fotoneja, joiden energia vastaa kahden energiatason erotusta. Koska fotonin energian E ja aallonpituuden λ välillä on yhteys , ovat vedyn spektriviivojen aallonpituudet
,
missä on vedyn Rydbergin vakio.
Bohrin postulaatti pyörimismäärän kvantittumisesta (postulaatti 2 yllä) selittää myös, miksei kiihtyvässä liikkeessä oleva elektroni putoa ytimeen säteillen energiansa pois.
Elektronin liike[muokkaa | muokkaa wikitekstiä]
Kaavasta (4) seuraa, että elektroni voi olla vain tietyillä säteillä. Mallin pohjalta voidaan teoreettisesti laskea myös elektronin nopeus ja kiertoaika, joskin kvanttimekaniikan myöhempi kehitys osoitti, ettei näillä suureilla ole oleellista merkitystä. Nopeudeksi saadaan:
- , missä e on alkeisvaraus, ε0 on tyhjiön permittiivisyys, h on Planckin vakio ja n elektronin radan järjestysluku.
ja kiertoajaksi
- .
Tasolla n = 1 elektronin nopeus on noin 2.2 x m/s, joka on noin sadasosa valonnopeudesta. Näin ollen vetyatomilla ensimmäiseen approksimaatioon ei tarvitse tehdä suhteellisuusteoreettisia korjauksia. Toisin on laita raskaammilla alkuaineilla, joiden valenssikuori on n = 6.
Bohrin atomimallin epäonnistuminen[muokkaa | muokkaa wikitekstiä]
Huolimatta Bohrin atomimallin onnistumisista, on se loppujen lopuksi epätarkka.
- Yllä oleva käsittely toimii vain vetyatomille, tai vedyn kaltaisille atomeille (atomeille, joilla on yksi elektroni). Kun atomissa on useampia elektroneita, vaikuttavat nämä keskenään, eivätkä kaikki elektronit enää koe ytimen täyttä varausta. Sallittujen kiertoratojen tarkka energia riippuukin kyseessä olevasta atomista. Energioiden selvittämiseksi joudumme laskemaan tietokoneella Schrödingerin yhtälön ratkaisuja tapauskohtaisesti.
- Atomiytimen massa ei ole ääretön verrattuna elektronin massaan. Tämän seurauksena ydin sekä elektroni kiertävät yhteistä massakeskipistettä, mikä vaatii korjauksia yllä oleviin kaavoihin.
- Postulaatti (3) väittää, etteivät klassisen mekaniikan lait päde kvanttihypyn aikana, muttei kuitenkaan kerro, minkä lakien pitäisi korvata pätemättömät klassisen mekaniikan lait.
- Postulaatti (2) väittää, että pyörimismäärä on kvantittunut, muttei selitä miksi.
- Teoria ei pysty ennustamaan siirtymien tapahtumistaajuuksia, eikä se kerro, ovatko kaikki mahdolliset siirtymiset sallittuja
- Teoria ei pysty selittämään molekyyleissä esiintyviä kemiallisia sidoksia
- Monet emissiospektriviivoista ovat itse asiassa kahdentuneet, kuten esimerkiksi natriumin D-viivat.
Askel Bohrin atomimallista eteenpäin[muokkaa | muokkaa wikitekstiä]
Bohrin malli tunnetaan joskus puoliklassisena mallina, koska vaikka se sisältääkin joitakin ajatuksia kvanttimekaniikasta, se ei ole täydellinen kvanttimekaaninen kuvaus atomista. Bohr teki kvanttimekanistisen hypoteesin pyörimismäärän kvantittoitumisesta, muttei mennyt pidemmälle.
Vuonna 1922 Bohr itse täydensi atomimalliaan eräillä lisäoletuksilla osoittaen, kuinka atomin rakenteen avulla voitiin selittää myös ne jaksolliseen järjestelmään liittyvät säännönmukaisuudet, jotka Mendelejev oli jo puoli vuosisataa aikaisemman havainnut eri alkuaineiden kemiallisissa ominaisuuksissa. Ennen vuotta 1922 oli jo todettu, että kunkin alkuaineen järjestysluku jaksollisessa järjestelmässä on sama kuin sen atomiytimen varaus alkeisvarausyksikköinä, ja näin ollen myös sama kuin sähköisesti neutraalissa atomissa olevien elektronien lukumäärä. Tämän vuoksi Bohr täydensi atomimalliaan olettamalla, että
- ydintä kiertävät elektronit täyttävät eri elektronikuoria järjestyksessä sisältä ulospäin,
- kullekin kuorelle mahtuu vain tietty määrä elektroneja ja että
- ionisoituessaan atomi pyrkii tilaan, jossa sen uloimmallakin kuorella on suurin mahdollinen määrä elektroneja.[1]
Oletusta (2) voitiin myöhemmin tarkentaa niin, että sen pohjalta muotoiltiin Paulin kieltosääntö, kun taas oletus (3) vastaa sitä, mikä nykyisin tunnetaan oktettisääntönä. Tältä pohjalta voitiin selittää ionisidoksen muodostuminen. Gilbert Newton Lewis täydensi teoriaa myöhemmin selittämällä kovalenttisen sidoksen muodostumisen.[2]
Täydelliseen atomin kuvaamiseen tarvitsee käyttää koko kvanttimekaniikan teoriaa, joka muotoutui useiden ihmisten työn tuloksena vuosia Bohrin mallin julkaisun jälkeen. Louis de Broglie esitti vuonna 1924 teorian, jonka mukaan elektronillakin on aaltoluonne, ja sille pätee sama liikemäärän (p) ja aallonpituuden ( välinen yhteys kuin fotonillekin (h on Planckin vakio). Aaltoluvun (k) avulla yhtälö voidaan esittää myös muodossa . Sijoittamalla tämän kaavaan (1) saamme , eli , jonka voimme tulkita seisovaksi aaltoliikkeeksi. Elektronin pyörimismäärän ja samalla energian kvantittuminen selittyy siten, että sen kiertoradalle eli ympyrän kehälle on mahduttava tietty kokonaislukumäärä elektronin aallonpituuksia, jolloin elektroni itse asiassa on seisova aalto. Koska seisova aaltoliike ei välitä energiaa, ei elektroni niin ollen säteile sähkömagneettista säteilyä, ja atomi on vakaa.
Tämä teoria pitää elektroneja aaltoina, jotka luovat 3-ulotteisia seisovan aallon kuvioita atomissa. Aineaallot keksi Louis de Broglie, ja oletettiin, että Bohrin atomimallissa sallittujen (stationaaristen) ratojen kehät olivat aineaaltojen aallonpituuksien monikertoja, mikä tarkoittaa sitä, että elektronien stationaariset radat ovat sellaisia, joilla ne muodostavat seisovia aaltoja. Tämä malli toimi kuitenkin vain vetyatomille.
Seuraava ja ratkaiseva askel oli Schrödingerin yhtälö, jossa hiukkasen tilaa kuvataan todennäköisyysaaltona.
Katso myös[muokkaa | muokkaa wikitekstiä]
Lähteet[muokkaa | muokkaa wikitekstiä]
- ↑ Reijo Rasinkangas: ”Bohr (1885–1962)”, Fysikaalisen maailmankuvan kehitys, s. 76–77. Oulun yliopiston fysikaalisten tieteiden laitos, 2005. Teoksen verkkoversio. (Arkistoitu – Internet Archive)
- ↑ Reijo Rasinkangas: ”Bohr (1885–1962)”, Fysikaalisen maailmankuvan kehitys, s. 77–78. Oulun yliopiston fysikaalisten tieteiden laitos, 2005. Teoksen verkkoversio. (Arkistoitu – Internet Archive)
Aiheesta muualla[muokkaa | muokkaa wikitekstiä]
- Opetus.tv: Kemian etäopiskeluympäristö, Bohrin atomimalli
- interactive demonstration (Arkistoitu – Internet Archive) elektronin todennäköisyyspilvistä vetyatomissa täydellisen kvanttimekaanisen ratkaisun mukaan.





























