Resultantti

Resultantti on voima, joka yksinään vaikuttaisi kappaleen liiketilaan samoin kuin kaksi tai useampi siihen vaikuttavaa voimaa yhdessä.

Kappaleen siirto­liikkeeseen vaikuttavien voimien resultantti saadaan laskemalla siihen vaikuttavat voimat yhteen vektorilaskennan sääntöjen mukaisesti. Tällainen voima vaikuttaisi kappaleen etenemis­liikkeeseen samoin kuin eri voimat yhdessä vaikuttavat. Sen sijaan kappaleen pyörimis­liikkeeseen vaikuttavien voimien resultanttia määritettäessä on otettava huomioon, että voimat saattavat vaikuttaa kappaleen eri kohdissa. Tietyissä tapauksissa niiden yhteis­vaikutus on sama, jonka yksi voima, resultantti, saisi aikaan vaikuttaessaan jossakin tietyssä pisteessä. Kaikissa tapauksissa voimien yhteis­vaikutusta ei kuitenkaan voida kuvata tällaisella resultantti­voimalla.

Jos voimat vaikuttavat pistemäiseen massaan tai kappaleeseen, jonka läpimitta on niin pieni, että sitä voidaan käytännössä pitää piste­mäisenä, ne voivat ainoastaan muuttaa sen nopeutta. Tässä tapauksessa voimien resultantti on aina sama kuin niiden vektori­summa, koska pyörimisliikettä ei esiinny.

Jos kappaleen läpimitta ei ole merkityksettömän pieni, voimat voivat muuttaa, paitsi kappaleen liike­tilaa, myös sen muotoa, esimerkiksi venyttää tai litistää sitä. Jos kyseessä kuitenkin on jäykkä kappale, jonka eri osien väliset etäisyydet ja näin ollen sen muoto eivät muutu, kappaleeseen vaikuttavat voimat voivat muuttaa sen kappaleen etenemis­liikkeen nopeutta eli sen massakeskipisteen nopeutta taikka sen pyörimis­liikkeen kulma­nopeutta.

Voimien yhteenlasku

Voimien yhteenlaskun kuvaaminen diagrammeilla. Vasemmalla suunnikassääntö, oikeanpuoleisessa kuvassa voimaa kuvaava jana on siirretty alkamaan toisen päästä.

Voima on vektorisuure, mikä merkitsee, että sillä on suuruus ja suunta, ja sille käytetään yleensä merkintää ${\vec {F}}$. Graafisesti sitä kuvataan suunnatulla janalla: voiman suunta vastaa janan suuntaa, ja sen suuruus on suoraan verrannollinen janan pituuteen; on vain päätettävä, kuinka monta newtonia vastaa yhtä sentti­metriä.

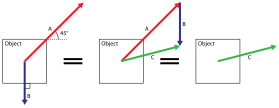
Vaikka vektori­­laskenta kehitettiin varsinaisesti vasta 1700- ja 1800-luvulla, on väitetty, että suunnikassääntö voimien yhteen­­laskemiseksi tunnettiin jo antiikin Kreikassa, ja joka tapauksessa sitä käyttivät Galilei ja Newton. Piirretään annetusta pisteestä alkamaan kaksi suunnattua janaa, jotka kuvaavat kappaleeseen vaikuttavia voimia, ja täydennetään kuvio suunnikkaaksi. Tällöin suunnikkaan lävistäjä kuvaa voimien vektorisummaa. Tämä on helppo käsittää intuitiivisesti: jos kokonaisvoiman ${\vec {F}}$ on kuvattava kahden voiman yhteistä vaikutusta kappaleeseen, sen suunnan on oltava lähempänä suuremman voiman suuntaa ${\vec {F}}_{2}$ , ja mikäli voimien suunnat ovat lähellä toisiaan, summavoiman on myös oltava suurempi kuin kumpikaan niistä erikseen. Että suunnikas­sääntö pitää tarkoin paikkansa, on sitä paitsi helposti osoitettavissa kokeellisesti. Resultantti voidaan likimääräisesti mitata diagrammista tai laskea tarkemmin trigonometrian avulla.

Paitsi suunnikas­säännöllä, voidaan sama tulos saada yksin­kertaisemmin myös siten, että toinen voimia kuvaavista janoista vain siirretään alkamaan toisen päästä kuten kuvassa oikealla kuten oikeanpuoleisessa kuvassa. Tällöin vektorien summaa vastaa jana, joka johtaa ensimmäisen janan alku­pisteestä jälkimmäisen loppu­pisteeseen. Kaavioiden ala­reunassa olevat kuvat vastaavat tapausta, jolloin voimat ovat saman- tai vastakkais­suuntaisia: saman­suuntaisten voimien suuruudet yksin­kertaisesti lasketaan yhteen, vastakkais­suuntaisista voimista taas suuremmasta vähennetään pienempi.

Vektorien yhteen­laskulla saatu voima on sellainen, joka yksinään vaikuttaessaan antaisi kappaleelle saman kiihtyvyyden, jonka se saa kaikkien huomioon otettujen voimien vaikuttaessa siihen. Jos voimat vaikuttavat kappaleen eri kohdissa, voimat yhdessä vaikuttavat kappaleen massakeskipisteen liikkeeseen samoin kuin niiden vektori­summan suuruinen voima vaikuttaisi. Ne voivat kuitenkin vaikuttaa myös kappaleen pyörimis­liikkeeseen, jolloin niiden vaikutus­pisteet on myös otettava huomioon.

Voimien vaikutus etenemis- ja pyörimisliikkeeseen

Vaikutuspiste

Kun voima vaikuttaa pieneen hiukkaseen, sen voidaan olettaa vaikuttavan vain yhdessä pisteessä, sillä hiukkasen tilavuus on merkityksettömän pieni. Hiukkanen on siis voiman vaikutus­piste. Silloin, kun voima vaikuttaa suurikokoiseen kappaleeseen, sen vaikutukset kappaleen pyörimis­liikkeeseen riippuvat siitä, mihin kohtaan kappaleessa voima vaikuttaa. Voimien yhteis­vaikutus voidaan määrittää seuraavilla tavoilla:

• Usein voima vaikuttaa kappaleessa niin pieneen kohtaan, että sen vaikutus­alue voidaan käsittää piste­mäiseksi. Tavallisesti on helppo päätellä, onko tästä aiheutuva virhe merkitsevä.
• Jos voima selvästi vaikuttaa koko kappaleeseen, kuten esimerkiksi painovoima, sen vaikutuksia voidaan kuvata korvaamalla se suurella joukolla pieniä voimia, joista kukin vaikuttaa vain yhteen pisteeseen, ja voiman vaikutukset voidaan laskea kussakin pisteessä erikseen. Tällöin kappale voidaan usein ajatella jaetuksi differentiaalisiin osiin, jolloin voidaan soveltaa integraalilaskentaa. Useissa tapauksissa voidaan kuitenkin osoittaa, että tulos on sama kuin jos koko voima vaikuttaisi vain yhdessä pisteessä; näin on laita esimerkiksi paino­voiman, jos painovoimakenttä on kappaleen jokaisessa kohdassa yhtä voimakas.

Joka tapauksessa jäykän kappaleen liiketilan analysointi on aloitettava olettamalla voimien vaikuttavan vain tietyissä pisteissä. Graafisesti kappaleeseen vaikuttavaa voimaa voidaan kuvata janalla, joka alkaa tästä vaikutuspisteestä.

Jäykkä kappale

Kuinka voima kiihdyttää kappaletta

Oikealla kuvatussa esimerkissä jäykkään kappaleeseen vaikuttaa vain yksi voima ${\vec {F}}$ pisteessä H. Kappaleen massa on $m$, ja sen massakeskipiste on C. Tällöin voima antaa kappaleelle, tarkemmin sanottuna sen massakeskipisteelle, kiihtyvyyden

${\vec {a}}={{\vec {F}} \over m}$,

mutta lisäksi kappale saa kulmakiihtyvyyden

${\vec {\alpha }}={{\vec {\tau }} \over I}$

Jälkimmäisessä yhtälössä ${\vec {\tau }}$ on voiman momentti, kun taas $I$ on kappaleen hitausmomentti. Voiman ${\vec {F}}$ momentti on vektorisuure, joka on määritettävä jonkin annetun pisteen suhteen seuraavasti:

${\vec {\tau }}={\vec {r}}\times {\vec {F}}$,

tai sen suuruus voidaan määrittää myös seuraavasti:

$\tau =Fk$.

Tässä vektori ${\vec {r}}$ on voiman vaikutuspisteen paikkavektori, kun origona on se piste, jonka suhteen momentti määritetään, usein (myös tässä esi­merkissä) kappaleen massakeskipiste. Oheisessa kuviossa tämä paikkavektori on piirretty kappaleen keskipisteestä voiman vaikutuspisteeseen. Jana $k$ taas on voiman vaikutus­suoran etäisyys massa­keski­pisteessä. (Jos kyseessä olisi vipu, tämä vastaisi vipu­varren pituutta.) Kuten kuviosta voidaan päätellä, voiman momentti ei muutu, jos sen vaikutus­pistettä siirretään sen vaikutussuoraa eli vaikutus­pisteen kautta kulkevaa voiman suuntaista suoraa pitkin, joka oheisessa kuviossa on merkitty mustalla katko­viivalla. Täsmällisemmin tämä voidaan osoittaa vektorien ristitulon ominaisuuksien vaulla, ja se osoittaa, että voiman vaikutus kappaleen pyörimis­liikkeeseen riippuu vain sen vaikutus­suoran sijainnista, ei siitä, missä vaikutus­suoran pisteessä voima vaikuttaa.

Momentti­vektori on kohti­suorassa voiman ja vektorin ${\vec {r}}$ määräämää tasoa vastaan, ja tässä esimerkissä se osoittaa kohti katsojaa. Myös kulma­kiihtyvyys­vektorin suunta on sama. Oikean käden säännön mukaisesti tällaisen vektorin suunta kohti katsojaa vastaa kierto­liikettä vastapäivään, suunta poispäin katsojasta taas kierto­liikettä myötäpäivään.

Kappaleen hitausmomentti $I$ on laskettava akselin suhteen, joka kulkee sen massa­keski­pisteen kautta ja on momentin suuntainen. Jos kappale on tasa­paksu homo­geeninen levy, kuten kuvion esimerkissä, sen hitaus­momentti on $I=mr^{2}/2$ . Jos sen massa on 0,5 kg ja säde 0,8 m, hitaus­momentti on siis 0,16 kgm². Jos siihen vaikuttava voima on 2 N ja vaikutus­suoran etäisyys massa­keski­pisteestä (vipu­varsi) 0,6 m, on voiman momentti 1,2 Nm. Se antaa kappaleelle kulma­kiihtyvyyden $\alpha =\tau /I=7,5{\frac {rad}{s^{2}}}$ ja sen massa­keski­pisteelle lineaarisen kiihtyvyyden a = F/m = 4 m/s².

Resultanttivoima

Resultanttivoiman graafinen määritys

Resultantti­voima on voima, jolla kaikki kappaleeseen vaikuttavat voimat voidaan ajatella korvattaviksi. Kun se voidaan määrittää, se tehdään seuraavien kahden vaiheen kautta:

1. Ensin lasketaan vektorisumma resultantti­voiman suuruuden ja suunnan määrittämiseksi;
2. Resultanttivoiman vaikutus­pisteen määrittämiseksi käytetään seuraavaa voimien momenteista saatua yhtälöä:

${\vec {r}}\times {\vec {F}}_{R}=\sum _{i=1}^{N}({\vec {r}}_{i}\times {\vec {F}}_{i})$

missä ${\vec {F}}_{R}$ on se kokonaisvoima, josta saadaan resultanttivoima, kun sille löydetään oikea vaikutus­piste ja sen paikka­vektori ${\vec {r}}$. Tässä kappaleeseen vaikuttavia eri voimia on merkitty ${\vec {F}}_{i}$ ja niiden vaikutus­pisteitä ${\vec {r}}_{i}$ . Kaikki momentit lasketaan saman, mieli­valtaisesti valitun pisteen suhteen.

Kaikissa tapauksissa tästä yhtälöstä ei voi ratkaista paikka­vektoria ${\vec {r}}$. Sellaisissa tapauksissa ei resultantti­voimaa voida määrittää, toisin sanoen ei voi olla sellaista yhteen pisteeseen vaikuttaavaa sellaista voimaa, joka yksinään vaikuttaisi kappaleen liike­tilaan samoin kuin siihen vaikuttavat eri voimat. Silloinkaan kun ${\vec {r}}$ voidaan laskea, se ei ole yksi­käsitteinen, sillä voiman vaikutuspistettä voidaan vapaasti siirtää sen vaikutussuoraa pitkin.

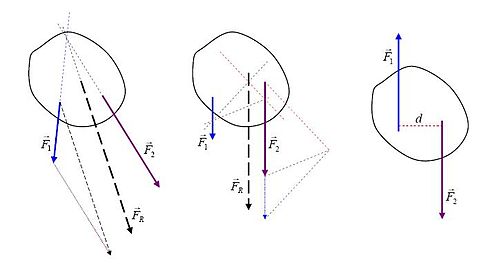
Oheisista kaavioista käy ilmi, miten resultantti­voiman vaikutussuora voidaan graafisesti määrittää, kun kaikkien voimien vaikutussuorat ovat samassa tasossa.

1. Vasemmanpuoleisessa kaavioissa voimien ${\vec {F}}_{1}$ ja ${\vec {F}}_{2}$ vaikutus­suorat leikkaavat toisensa. Kun voima­vektorit on laskettu yhteen, resultantiksi saadaan tämän vektorisumman suuruinen voima, jonka vaikutus­pisteenä on näiden vaikutussuorien leikkauspiste. Kaikkien voimien momentit tämän pisteen suhteen ovat nollia, ja myös resultantti­voiman momentti minkä tahansa pisteen suhteen on eri voimien momenttien summa saman pisteen suhteen.
2. Keskimmäisessä kaaviossa voimat ovat yhden­suuntaisia. Kun voimat on laskettu yhteen, saadun voiman vaikutus­piste sijoitetaan suoralle, jossa se vastaa resultanttivoimaa ${\vec {F}}_{R}$. Tämä tehdään jakamalla kukin voima komponentteihin, joiden vaikutus­suorat (vaaleat katkoviivat) leikkaavat yhdessä pisteessä, joka tässä on sijoitettu kaavion oikealle puolelle.
3. Oikean­puoleisessa kaaviossa kappaleeseen vaikuttaa kaksi yhtä suurta, mutta vastakkais­suuntaista voimaa. Niiden yhteis­vaikutus kappaleen etenemis­liikkeeseen on nolla, mutta niiden yhdessä aikaansaama momentti on $\tau =Fd$, missä $\ d$  on niiden vaikutussuorien välinen etäisyys. Tämä on niin sanottu "puhdas" momentti, sillä resultantti­voima on nolla. Tällaisten voimien sanotaan muodostavan voimaparin.

Erikoistapauksia

Vaikutuspiste kappaleen ulkopuolella

Vaikutussuorien leikkaus­pisteenä määritetty resultantti­voiman vaikutuspiste saattaa olla myös kappaleen ulkopuolella. Tällaisissa tapauksissa se voidaan usein ajatella siirrettäväksi vaikutus­suoraansa pitkin kappaleen sisä­puolelle. Toisinaan tämä ei kuitenkaan ole mahdollista, sillä vaikutussuora ei kulje kappaleen läpi. Näin saattaa tapahtua esi­merkiksi, jos kappale on renkaan muotoinen ja vaikutus­suora kulkee sen keskellä olevan reiän kautta. Tällaisissa tapauksissa ei voima­systeemiä voida korvata yhdellä voimalla.

Yhdensuuntaiset voimat ja voimapari

Kun voimat ovat yhden­suuntaisia, voidaan valita jokin niitä vastaan kohti­suora taso, johon vaikutus­pisteet sijoitetaan. Jos voimia on vain kaksi, F¹ ja F², voidaan koordinaatisto valita niin, että nämä molemmat ovat x-akselilla, pisteissä x¹ ja x². Tällöin voimien resultantin vaikutus­piste on

${\frac {F_{1}x_{1}+F_{2}x_{2}}{F_{1}+F_{2}}}$

Tämä lauseke pätee myös, jos voimat ovat vastakkais­suuntaisia. Tällöin on kuitenkin jompi­kumpi voimista ajateltava negatiiviseksi. Jos vastakkais­suuntaiset voimat kuitenkin ovat itseis­arvoltaan yhtä suuria, ei näin voida menetellä, koska lausekkeen nimittäjä saa arvon nolla. Tällöin on kyseessä voimapari, jolle ei voida määrittää resultanttia.

Resultanttia ei aina ole

Jos voimien vaikutus­­suorat eivät leikkaa toisiaan eivätkä ole yhden­­suuntaisia, toisin sanoen ne eivät ole samassa tasossa, voimien yhteis­vaikutusta ei myöskään yleensä voida ollenkaan kuvata yhdellä resultantantti­voimalla.

Vaikka resultantti­voimaa ei kaikissa tapauksissa voida määrittää, jäykkään kappaleeseen vaikuttavat voimat voidaan aina ajatella korvattavaksi yhdellä voimalla sekä yhdellä "puhtaalla" momentilla. Tällöin tämä voima saadaan vektorien yhteen­laskuna, mutta momentin laskemiseksi tämä summa­voima on sijoitettava tietylle vaikutussuoralle. Tämä vaikutus­suora voidaan valita mieli­valtaisesti, mutta "puhdas" momentti riippuu sen vaikutuksesta. Jos on mahdollista valita sellainen vaikutus­suora, että tästä aiheutuva ylimääräinen momentti tulee nollaksi, voimat voidaan ajatella korvattavaksi resultantti­voimalla, joka saadaan voima­­vektorien summana.

Käytäntö

Vektorikaavio muiden kuin yhdensuuntaisten voimien yhteenlaskemiseksi

Vektorikaavio yhdensuuntaisten voimien yhteenlaskemiseksi

Vaikka resultantti­voimaa ei voida määrittää läheskään kaikille voima­systeemeille, se on käsitteellisesti merkittävä ja myös monissa käytännön sovelluksissa käyttö­kelpoinen käsite. Kun voimat voidaan korvata yhdellä resultantti­voimalla, kuten on laita monissa tasomaisissa systeemeissä, tämä yksin­kertaistaa suuresti käytännön laskuja. Toisaalta resultantin käsite on osoitus siitä, että voimien yhteis­vaikutusta ei aina voida kuvata yksin­kertaisesti laskemalla ne vektoreina yhteen, sillä ne eivät välttämättä vaikuta samassa pisteessä.