Tiheysfunktio

Tiheysfunktio [1][2][3] (engl. probability density function [4]) on todennäköisyyslaskennassa ja tilastotieteessä jatkuvan satunnaismuuttujan todennäköisyyden jakautumista kuvaava todennäköisyysfunktio. Tiheysfunktiolla on läheinen yhteys tilastotieteessä käytettävään histogrammiin, jolla havainnollistetaan luokitellun aineiston arvojen jakautumista. Tiheysfunktioiden arvot eivät itsessään ole todennäköisyyksiä, mutta tiheysfunktion avulla voidaan laskea todennäköisyydet käyttämällä määrättyä integraalia. Tiheysfunktio määrittelee satunnaismuuttujan täysin, ja sen avulla voidaan määrittää satunnaismuuttujan kaikki ominaisuudet.[1][2][5][6]
Nimityksistä[muokkaa | muokkaa wikitekstiä]
Satunnaismuuttujan todennäköisyysfunktio on tiheysfunktiolle yläkäsite, jossa diskreetin satunnaismuuttujan pistetodennäköisyysfunktio on tiheysfunktiolle rinnakkaiskäsite. Tiheys- ja pistetodennäköisyysfunktioilla on varsin erilaiset ominaisuudet ja matemaattiset vaatimukset, joten on perusteltua kutsuakin näitä eri nimillä. Tiheysfunktion nimitykset muilla kielillä ovat suomalaisen nimityksen kanssa vastaavia, mikä voidaan todeta esimerkiksi engl. probability density function (eli PDF), saks. Wahrscheinlichkeitsdichtefunktion (eli WDF) tai ransk. densité de probabilité.
Tiheysfunktiota kutsutaan joskus myös todennäköisyyden massafunktioksi, jotta nimityksen mieleyhtymä todennäköisyyden kasautumisesta tietyille arvoalueille korostuisi. Samaa yritetään kenties tiheys-sanan käytöllä. Muutamilla muilla käsitteillä, kuten esimerkiksi momenteilla, etsitään kenties vertailukohtia mekaniikasta.
Normaalijakauman tiheysfunktion kuvaajaa kutsutaan yleisesti "kellokäyräksi" tai "Gaussin käyräksi".
Määritelmä[muokkaa | muokkaa wikitekstiä]
Satunnaismuuttuja on jatkuva, jos on olemassa sellainen funktio , että kaikille reaaliakselin väleille on
- .
Tätä funktiota kutsutaan tiheysfunktioksi. Satunnaismuuttujan jatkuvuuden edellytys on, että mitkä tahansa todennäköisyydet tulee voida laskea tiheysfunktion määrättyjen integraalien avulla yksikäsitteisellä tavalla. Samalla käy ilmi tiheysfunktion kytkentä todennäköisyyteen.[7][5][4]
Kukin yksittäinen satunnaismuuttujan arvo on alkeistapaus. Kaikki mahdolliset alkeistapaukset muodostavat yhdessä perusjoukon. Kun ajatellaan tiheysfunktiota, on sen määrittelyjoukko ja satunnaismuuttujan perusjoukko sama joukko. Yksittäiset määrittelyjoukon kohdat ovat satunnaismuuttujan alkeistapauksia. Tapahtumaa, joka koostuu usein useista alkeistapauksista, merkitään tavallisesti lukujoukkona esimerkiksi lukuvälinä. Lukuvälit rajaavat perusjoukosta suuren osan alkeistapauksista itseensä ja loput perusjoukon alkeistapauksista muodostavat vastatapahtuman. Määritelmä esittää, miten lukuvälin arvojen muodostama tapahtumasta voidaan laskea sen todennäköisyys.
Tiheysfunktio voidaan määritellä myös kertymäfunktion (katso alla) derivaattanakin
mikäli se vain on derivoituva funktio.
Kertymä- eli jakaumafunktio[muokkaa | muokkaa wikitekstiä]
- Pääartikkeli: Kertymäfunktio
Todennäköisyyksien laskemiseksi tulee tiheysfunktiosta ottaa määrätty integraali. Tämä voi tulla vaivalloiseksi tai se voi olla jopa mahdotontakin, sillä kaikille tiheysfunktioille integraalia ei voida määrittää lausekkeen muodossa (esimerkiksi normaalijakauma). Näiden tapausten todennäköisyydet lasketaan numeerisen analyysin avulla likiarvoina ja tulokset kootaan taulukoiksi.[8]
Toistuvan integroimisen välttää antamalla todennäköisyydet valmiiksi integroituna lausekkeena, jota kutsutaan kertymäfunktioksi . Kertymäfunktion avulla todennäköisyydet saadaan funktioiden arvojen aritmeettisilla laskutoimituksilla. Yleisin tapa on määrittää todennäköisyys tapahtumana, joka sisältää alkeistapaukset tiettyyn arvoon asti:
Esimerkiksi eksponenttijakaumassa satunnaismuuttujan tiheysfunktio on
joka on määritelty . Sen kertymäfunktio saadaan määritettyä integroimalla se ensin välin yli
Kun ylärajaksi merkitään , saadaan kertymäfunktion lauseke
Kertymäfunktiolla voidaan nyt laskea todennäköisyys integroimatta kertaakaan (parametrilla )
Vaikka kertymäfunktio on todennäköisyyksien laskemisessa käytännöllisempi, tarvitaan tiheysfunktiota edelleen tunnuslukujen laskemisessa.
Esimerkki[muokkaa | muokkaa wikitekstiä]

Tasaisen jatkuvan jakauman tiheysfunktio saa saman arvon kaikkialla perusjoukkonsa alueella. Mitä leveämpi on perusjoukko, sen pienempiä ovat tiheysfunktion arvot. Jos tiheysfunktio saa arvoja väliltä , tulee tiheysfunktion arvoksi 0,25, sillä Tasaisen jakauman tiheysfunktion arvot välillä ovat aina välin pituuden käänteisluku eli .[1]
Yhteys tilastotieteeseen[muokkaa | muokkaa wikitekstiä]

Tiheysfunktio voidaan ajatella syntyvän satunnaismuuttujan antamien arvojen eli ulostulojen tilastollisesta histogrammista. Kun ulostulojen määrää kasvatetaan hyvin suureksi, voidaan luokittelua tihentää ja silloin pylväistä tulee hyvin kapeita. Kapeiden pylväiden yläpäät piirtävät melko sileän käyrän, joka tulee pylväiden kaventamisprosessin edetessä lähestymään tiheysfunktiota. Tiheysfunktio edustaa sellaista "histogrammia", jossa on ääretön määrä ulostuloja ja olemattoman kapeat luokat. Histogrammilla voidaan laskea prosentteina erilaisien tapahtumien osuuksia, joita voidaan tulkita tilastollisen todennäköisyyden tulkinnan mukaan todennäköisyyksien likiarvoiksi. Histogrammin alue ja tiheysfunktion alle jäävä alue voidaan siten tulkita samaksi asiaksi. Pinta-alaa, joka jää tiheysfunktion käyrän alle, kutsutaan joskus "todennäköisyysmassaksi". Tiheysfunktion arvo tietyssä kohdassa kertoo vain "todennäköisyysmassan" korkeuden kyseisessä kohdassa x-akselia.[1][2][5]
Ominaisuuksia[muokkaa | muokkaa wikitekstiä]
Ei-negatiivisuus ja epäjatkuvuuskohdat[muokkaa | muokkaa wikitekstiä]
Tiheysfunktiolta vaaditaan yleisesti, että
kaikille reaaliluvuille. Tämä varmistaa sen, että määrätyt integraalit eli todennäköisyydet olisivat positiivisia tai ainakin ei-negatiivisia.[7][1]
Määrätyn integraalin ominaisuuksista johtuen funktion äärellinen määrä epäjatkuvuuskohtia ei vielä estä integraalin laskemista. Integraalilaskennossa jokainen yksittäisen pisteen integraali saa arvokseen nolla, joten äärellinen määrä puuttuvia pisteitä ei pienennä määrätyn integraalin arvoa. Asia muuttuu silloin, jos epäjätkuvuuskohtia on numeroituvasti tai ylinumeroituvasti ääretön määrä.[6]
Normitus[muokkaa | muokkaa wikitekstiä]
Mikä tahansa funktio ei voi olla tiheysfunktio. Ei-negatiivisuuden lisäksi tiheysfunktion avulla muodostettavat todennäköisyydet tulisivat kaikki olla satunnaismuuttujan todennäköisyyksien mukaisia. Tämä ominaisuus johtaa myös siihen, että koko perusjoukon sisältävän välin todennäköisyys ja samalla tiheysfunktion määrätyn integraalin arvo tällä välillä on yksi:[5][1][6][4]
Tämä ehto normittaa funktion. Eräissä tapauksissa jälkimmäinen päätepiste voi olla ääretön tai ensimmäinen päätepiste voi olla "miinus ääretön". Silloin tulee myös epäoleellinen integraali toteuttaa ehdon [1][4]
Yksittäisen pisteen todennäköisyys[muokkaa | muokkaa wikitekstiä]
Diskreetin satunnaismuuttujan kullakin yksittäisellä arvolla on nollasta poikkeava todennäköisyys. Tämä johtuu satunnaismuuttujan perusjoukon äärellisestä tai numeroituvasti äärettömästä koosta. Tämän perusteella kukin lukuarvo esiintyy "kohtuullisen" usein satunnaismuuttujan ulostulojen joukossa. Jatkuvan satunnaismuuttujan jakaumassa mahdollisia reaalilukuarvoisia arvoja on ylinumeroituvasti ääretön määrä, jolloin yksittäisen lukuarvon esiintyminen on "äärimmäisen harvinaista". Usein tulkitaankin, että sen esiintymistodennäköisyys on "nolla". Tässä on kuitenkin ristiriita käytännön kanssa, sillä satunnaismuuttujahan antaa aina tulokseksi joitakin lukuarvoja. Ainakaan näiden arvojen todennäköisyys ei voi olla "tasan nolla", sillä silloinhan niitä ei esiintyisi ollenkaan. Koska yksittäiset satunnaismuuttujan arvot ovat selvästi mahdollisia, mutta kuitenkin äärimmäisen epätodennäköisiä, voi niiden todennäköisyyttä pitää "melkein nollana". Syntyvä paradoksi kierretään välttämällä jatkuvien satunnaismuuttujien tapauksissa yksittäisten tapauksien todennäköisyyksien laskemista ja summaamista.
Todennäköisyyksiä lasketaankin vain tapahtumille, jotka muodostavat lukusuoralla välejä . Todennäköisyys, että seuraava satunnaismuuttujan arvo on jokin välin sisältävistä luvuista, lasketaan määrättyllä integraalilla [9]
Huomaa, että edellisen selostuksen nojalla voidaan pitää seuraavia todennäköisyyksiä yhtäsuurina:
sillä avoimella välillä puuttuvan päätepisteen lisäys on todennäköisyydessä vain "nollan" lisäämistä tulokseen. Tämän ymmärtää helposti määrätyn integraalin ominaisuudesta, jossa
Integraalin sisältävä määritelmä on käytännöllinen myös sen vuoksi, että se sallii tiheysfunktiolle joitakin yksittäisiä, eli äärellisen määrän, epäjatkuvuuskohtia ilman, että integraalin laskemisessa tulisi ongelmia.[9]
Epäoleellinen integraali[muokkaa | muokkaa wikitekstiä]
Jos epäoleelliset integraalit ovat olemassa, voidaan laskea myös
Todennäköisyys, että seuraava satunnaismuuttujan arvo on jokin perusjoukon luvuista, on luonnollisesti yksi (tapahtuu aina). Välin rajat voidaan merkitä äärettömän kauaksi toisistaan, vaikka perusjoukko voikin olla rajoitettu. Tällöin [10][9]
raja-arvon määrittämässä mielessä.
Tunnuslukuja: Momentit[muokkaa | muokkaa wikitekstiä]
- Pääartikkeli: Momentti
Jatkuvien satunnaismuuttujien jakaumien tunnuslukuja on lukuisia. Odotusarvo merkitään ja määritellään [6]
Kyseessä on epäoleellinen integraali ja se on olemassa vain, kun se suppenee itseisesti. Mikäli perusjoukko on rajoitettu esimerkiksi välille , voidaan odotusarvo laskea määrätyllä integraalilla
Odotusarvoa kutsutaan myös ensimmäiseksi momentiksi, sillä se on ensimmäinen pitkässä momenttien sarjassa. Yleinen määritelmä n:nelle momentille on [11]
Keskusmomenteiksi tai keskeismomentiksi kutsutaan niitä odostusarvoja, jotka lasketaan erotuksista Ne määritellään muuten samalla tavalla kuin tavalliset momentit eli origomomentit: [11][10]
Näistä toinen keskusmomentti on varianssi:[6][10]
josta saadaan neliöjuurella keskihajonta
Kaikki momentit saadaan momentit generoivasta funktiosta [10]
Tiheysfunktion kuvaajia[muokkaa | muokkaa wikitekstiä]
-
Beta-jakauman odotusarvon sijainti
-
Burrin jakaumia eri parametreillä
-
Cauchyn jakaumia eri parametreillä
-
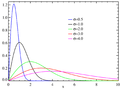
Eksponenttijakaumia kolmella parametrillä
-
Frechet-jakaumia eri parametreillä
-
Gammajakaumia eri parametreillä
-
Maxwell-Boltzmannin jakaumia eri parametreillä
-
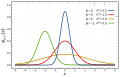
Normaalijakaumia neljällä parametriparilla
-
Pareto-jakaumia eri parametreillä
-
Rayleigh-jakaumia eri parametreillä
Lähteet[muokkaa | muokkaa wikitekstiä]
- ↑ a b c d e f g Kivelä, Simo K.: Jatkuvat jakaumat, M niin kuin matematiikka, 10.8.2000
- ↑ a b c Alatupa, Sami et al.: Pitkä Sigma 6, s. 6−41. (lukion pitkän matematiikan oppikirja). Helsinki: Otava, 2010. ISBN 978-951-31-5343-4.
- ↑ Ruskeapää, Heikki: Todennäköisyyslaskenta I (Arkistoitu – Internet Archive)(luentomoniste), Turun Yliopisto, 2012
- ↑ a b c d e Weisstein, Eric W.: Probability Density Function (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)
- ↑ a b c d Alatupa, Sami et al.: Pitkä Sigma 6, s. 153−180. (lukion pitkän matematiikan oppikirja). Helsinki: Otava, 2010. ISBN 978-951-31-5343-4.
- ↑ a b c d e Etälukio: Jatkuva jakauma (Arkistoitu – Internet Archive)
- ↑ a b Emet, Stefan: Johdatus todennäköisyyslaskentaan ja tilastotieteeseen (Arkistoitu – Internet Archive), Matematiikan ja tilastotieteen laitos, Turun Yliopisto, 2014
- ↑ Alatupa, Sami et al.: Pitkä Sigma 6, s. 164−. (lukion pitkän matematiikan oppikirja). Helsinki: Otava, 2010. ISBN 978-951-31-5343-4.
- ↑ a b c Alatupa, Sami et al.: Pitkä Sigma 6, s. 154−164. (lukion pitkän matematiikan oppikirja). Helsinki: Otava, 2010. ISBN 978-951-31-5343-4.
- ↑ a b c d e Saarnisaari, Harri (Arkistoitu – Internet Archive): Satunnaismuuttujat (Arkistoitu – Internet Archive) (luentomateriaalia), 2003
- ↑ a b c d Liski, Erkki: Luku 5 Jatkuvat jakaumat, s. 151–160, luennosta Matemaattinen tilastotiede, Tampereen yliopisto, 2005
- ↑ Kivelä, Simo K.: Jakauman tunnusluvut, M niin kuin matematiikka, 10.8.2000
Aiheesta muualla[muokkaa | muokkaa wikitekstiä]
- Weisstein, Eric W.: Continuous Distribution (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)



![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)








![{\displaystyle [0,a]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/63d050b0ffe6cc6f635808b9a013366a60e6d0c0)





![{\displaystyle [4,8]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4174b8055e90e2ed020453ec5bcee7ee1b3bfab3)



![{\displaystyle \Omega :=[a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/10c8f59bab3997cd2f186459f7a68573222958de)


![{\displaystyle \scriptstyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97afd7fabf45690bb3a6512b519f47b477a9a9c6)






![{\displaystyle \mu =m_{x}=\operatorname {E} [X]=\int _{-\infty }^{\infty }xf(x)\,\mathrm {d} x.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/618a1c0cd9d2355a36c52717aed738c8dcda6ba7)
![{\displaystyle \operatorname {E} [X]=\int _{a}^{b}xf(x)\,\mathrm {d} x.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a2ae5a3104d93d2ef9b5ed32861a4b4ec01ccca)
![{\displaystyle \mu _{n}=\operatorname {E} [X^{n}]=\int _{-\infty }^{\infty }x^{n}f(x)\,\mathrm {d} x.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0714c8c8272e74e48fb42428729c2e33e1f129ed)

![{\displaystyle \mu _{n}'=\operatorname {E} [(X-\mu )^{n}]=\int _{-\infty }^{\infty }(x-\mu )^{n}f(x)\,\mathrm {d} x.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4a8980e455a383d15d812ab3c3aba2b08ad2a16)
![{\displaystyle \mu _{2}'=\operatorname {E} [(X-\mu )^{2}]=\int _{-\infty }^{\infty }(x-\mu )^{2}f(x)\,\mathrm {d} x=\sigma ^{2}=Var(X),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cdcaa4083273df855cb712c1e6cb327bac69c79a)