Riemannin pinta
| Tähän artikkeliin tai sen osaan on merkitty lähteitä, mutta niihin ei viitata. Älä poista mallinetta ennen kuin viitteet on lisätty. Voit auttaa Wikipediaa lisäämällä artikkelille asianmukaisia viitteitä. Lähteettömät tiedot voidaan kyseenalaistaa tai poistaa. |
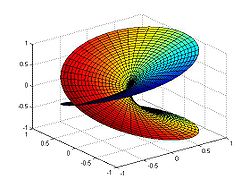
Matematiikassa Riemannin pinta, nimetty matemaatikko Bernhard Riemannin mukaan, on 1-ulotteinen kompleksimonisto (eli 2-ulotteinen monisto). Riemannin pintojen voidaan ajatella olevan "epämuodostuneita" versioita kompleksitasosta: paikallisesti, jokaisen pisteen ympäristössä, ne näyttävät kompleksitasolta, mutta globaali topologia voi olla hyvinkin erilainen.
Riemannin pinnat ovat kätevä tapa tutkia useita moniarvoisia funktioita, sillä sopivalla Riemannin pinnalla tällaisesta funktiosta voidaan tehdä yksikäsitteinen. Esimerkkejä kyseisistä funktioista ovat neliöjuuri ja logaritmi.
Mille tahansa kompleksitasossa tai sen avoimelle osajoukolle määritellylle analyyttiselle funktiolle f (moniarvoinen tai yksikäsitteinen) on olemassa Riemannin pinnalla määritelty analyyttinen ja yksikäsitteinen funktio g, siten että g vastaa funktiota f tietyin rajoituksin. Riemannin pinnat ovat siis hyödyllisiä analyyttisten funktioiden tutkimiseen.
Määritelmä[muokkaa | muokkaa wikitekstiä]
Riemannin pinta voidaan määritellä usealla ekvivalentilla tavalla. Tässä muutama:
- Mikä tahansa 1-ulotteinen kompleksimonisto on Riemannin pinta . Tämä tarkoittaa sitä, että Riemannin pinta on Hausdorffin avaruus, jolla tiettyjen avointen osajoukkojen ja kompleksitason avointen osajoukkojen välillä on kokoelma Φ homeomorfismeja, jotka toteuttavat ehdot:
- Jokainen Riemannin pinnan piste kuuluu ainakin yhden homeomorfismin määrittelyjoukkoon.
- Jos kahden homeomorfismin määrittelyjoukot menevät päällekkäin, niin yhdistetty kuvaus on analyyttinen.
- Riemannin pinta on pinta, jolla on konformi struktuuri.
Esimerkkejä[muokkaa | muokkaa wikitekstiä]

- Kompleksitaso C on yksinkertaisin esimerkki Riemannin pinnasta.
- Analogisesti, jokainen kompleksitason avoin osajoukko on Riemannin pinta. Yleisemmin, jokainen Riemannin pinnan avoin osajoukko on Riemannin pinta.
- Olkoon S = C ∪ {∞} ja f(z) = z, missä z kuuluu joukkoon S \ {∞} ja g(z) = 1 / z missä z kuuluu joukkoon S \ {0} sekä 1/∞ määritellään olemaan 0. Tällöin funktiot f ja g määrittävät Riemannin pinnan S. Tätä Riemannin pintaa kutsutaan Riemannin palloksi. Tämä on esimerkki kompaktista Riemannin pinnasta.

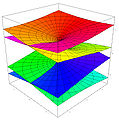
- Esimerkkejä Riemannin pinnoista. Kuvissa väri edustaa neljättä ulottuvuutta. Kuvat ovat projektioita 4-ulotteisesta avaruudesta 3-ulotteiseen avaruuteen. Vaikka nämä Riemannin pinnat "elävätkin" neljäulotteisessa avaruudessa, ne voidaan kuitenkin upottaa tasoon.
Riemannin pinnan konstruktio neliöjuurifunktiolle[muokkaa | muokkaa wikitekstiä]
Tämä konstruktio ei ole matemaattisesti kovin eksakti, mutta valottaa ehkä ajatusta Riemannin pintojen takana.
Funktio ei ole yksikäsitteinen, vaan se saa jokaisessa pisteessä kaksi eri arvoa. Nimittäin jokainen kompleksiluku z voidaan ilmoittaa muodossa , tällöin . Siispä kun z kulkee yhden kierroksen (r-säteistä ympyrää pitkin) niin kulkee vain puolikierrosta.
Neliöjuurifunktiolla on siis kaksi haaraa. Tästä ongelmasta päästään eroon rajoittamalla argumentti esimerkiksi välille . Jatkuvuudessa kuitenkin ongelma säilyy. Riemannin ajatus oli ottaa niin monta kopioita kompleksitasosta, kuin funktiolla on haaroja. Eli tässä tapauksessa kaksi. Nämä kopiot asetetaan päällekkäin ja leikataan tasot haaroja pitkin (neliöjuuren tapauksessa negatiivista tai positiivista reaaliakselia pitkin). Leikataan siis molemmista tasoista negatiivista reaaliakselia pitkin.
Nyt liimataan ylemmän kompleksitason toisen neljänneksen leikkausreuna alemman kompleksitason kolmannen neljänneksen leikkausreunaan. Liimataan vielä ylemmän kompleksitason kolmannen neljänneksen leikkausreuna alemman tason toisen neljänneksen leikkausreunaan (kuvassa keltaiset reunat liimataan yhteen ja punaiset reunat liimataan yhteen).

Näin on saatu aikaan pinta, joka itse asiassa on Riemannin pinta. Tällä Riemannin pinnalla voidaan määritellä uusi neliöjuurifunktio, joka on yksikäsitteinen - nyt voidaan nimittäin erottaa ne pisteet toisistaan, joissa neliöjuurifunktio sai kaksi eri arvoa. Eli funktio saakin kaksi eri arvoa kahdessa eri pisteessä. Tämä johtuu siitä, että täyden kierroksen kulkeminen uudella pinnalla vaatii molempien kompleksitasojen kierrosten läpikäymistä. Pisteet voidaan siis erottaa kierrosluvun perusteella (ensimmäinen kierros ja toinen kierros). Mielivaltainen luku löytyy molemmilta kompleksitasoilta samasta kohtaa, mutta tässä konstruktiossa ne ovat eri pisteet (sillä ne ovat "eri kerroksessa"). Tarkempi tarkastelu osoittaisi, että neliöjuurifunktio on myös analyyttinen ja siis myös jatkuva tällä Riemannin pinnalla.

Riemannin pintojen luokittelu[muokkaa | muokkaa wikitekstiä]
Riemannin pinnat voidaan luokitella kolmeen eri luokkaan: hyperbolisiin, parabolisiin ja elliptisiin Riemannin pintoihin. Geometrisesti nämä vastaavat negatiivista kaarevuutta, nolla kaarevuutta ja positiivista kaarevuutta.
Elliptiset Riemannin pinnat[muokkaa | muokkaa wikitekstiä]
Määritelmän mukaan, pinta X, jonka vakio kaarevuus on +1, on elliptinen. Riemannin pallo C ∪ {∞} on ainoa esimerkki.
Paraboliset Riemannin pinnat[muokkaa | muokkaa wikitekstiä]
Määritelmän mukaan nämä ovat ne pinnat X, joiden vakio kaarevuus on 0. Tällöin on kolme mahdollisuutta X:lle. Se voi olla kompleksitaso, punkteerattu kompleksitaso tai torus
Hyperboliset Riemannin pinnat[muokkaa | muokkaa wikitekstiä]
Riemannin pinnat joiden kaarevuus on −1 kutsutaan hyperbolisiksi. Tämä luokka on isoin näistä kolmesta.
Lähteet[muokkaa | muokkaa wikitekstiä]
- http://planetmath.org/encyclopedia/RiemannSurface.html (Arkistoitu – Internet Archive)
- Ahlfors, Lars & Sario, Leo: Rieman surfaces, 2. painos, Princeton university press, 1960.
Kirjallisuutta[muokkaa | muokkaa wikitekstiä]
- Väisälä, Kalle: Matematiikka IV. 141, 10. painos. Espoo: Otakustantamo, 1986 (1965). ISBN 951-671-087-5.