Riemannin pallo

Stereografisella projektiolla laajennettu kompleksitaso voidaan kuvata Riemannin pallolle tai päinvastoin.

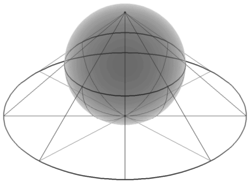
Riemannin pallo on kompleksitason yläpuolella sijaitseva pallo, joka sivuaa kompleksitasoa origossa. Pallon hyödyllisyys ilmenee siitä, että jokainen kompleksitason piste voidaan projisoida pallolle stereografisella projektiolla ja kääntäen jokainen pallonpinnan piste voidaan projisoida kompleksitasolle, lukuun ottamatta sitä pistettä, joka sijaitsee täsmälleen vastakkaisella puolella pallon keskipistettä kuin sivuamispiste. Jos kompleksitasoon kuitenkin lisätään yksi piste, äärettömyyspiste $\infty$, jonka ajatellaan sijaitsevan äärettömän kaukana missä suunnassa tahansa, Riemannin pallon jokaista pistettä vastaa yksi piste tällä ns. laajennetulla tasolla ja kääntäen. Näin saatu avaruus on kompakti, ja sitä käytetään funktioteoriassa yleisesti funktioiden määrittelyjoukkona.

Tason ja pallon pisteiden vastaavuus

Kompleksitason pisteen kuvaus sterografisella projektiolla pallonpinnalle.

Riemannin pallo voidaan käsittää kolmiulotteisessa avaruudessa $\mathbb {R} ^{3}$ olevaksi origokeskeiseksi palloksi, jolloin sen yhtälö on

$x^{2}+y^{2}+z^{2}=1$

Toisaalta jokaista kompleksilukua x + yi vastaa tason piste (x,y). Kutakin kompleksilukua vastaa Riemannin pallolla piste, jossa pisteestä (x, y, 0) pisteeseen (0,0,1) piirretty jana leikkaa pallon pinnan. Tämän pisteen karteesiset koordinaatit ovat

$\left({\frac {2x}{1+x^{2}+y^{2}}},{\frac {2y}{1+x^{2}+y^{2}}},{\frac {-1+x^{2}+y^{2}}{1+x^{2}+y^{2}}}\right).$

Kääntäen pallon pinnalla olevaa pistettä (x, y, z) kompleksitasolla vastaava piste on

$\left({\frac {x}{1-z}},{\frac {y}{1-z}}\right)$

eli kompleksilukuna

$\left({\frac {x}{1-z}}+i{\frac {y}{1-z}}\right)$.

Toisaalta tason pisteet voidaan esittää myös napakoordinaateissa muodossa $\left(R,\theta \right)$, missä $R$ merkitsee pisteen etäisyyttä origosta ja $\theta$ ($0<=\theta <=2\pi$) osoittaa, missä suunnassa se on origosta katsottuna. Täten jokainen kompleksiluku voidaan esittää myös muodossa $Rcos\theta +iRsin\theta$ tai Eulerin kaavojen mukaisesti lyhemmin muodossa $Re^{i\theta }$. Vastaavasti pallopinnan pisteet voidaan esittää myös pallokoordinaattien (φ, θ) avulla, jotka määritellään samaan tapaan kuin maapallon leveys- ja pituusasteet; yksikkönä kuitenkin käytetään radiaania. Tällöin $\varphi$ ($0<\varphi <2\pi$ vastaa leveys- ja $\Theta$ ($-{\frac {\pi }{2}}<\Theta <{\frac {\pi }{2}}$) pituuspiiriä. Näin tehtäessä kutakin pallon pistettä ($\varphi ,\Theta$ ) vastaa tasolla piste

$(R,\Theta )=\left({\frac {\cos \varphi }{1-\sin \varphi }},\Theta \right),$

ja kääntäen kutakin tason pistettä $(R,\Theta )$ vastaa pallon pinnalla piste

$(\varphi ,\Theta )=\left(2\arctan \left({\frac {1}{R}}\right)-{\frac {\pi }{2}},\Theta \right).$

Täten jokainen kompleksiluku, joka kompleksitasolla on samalla etäisyydellä origosta eli jolla on sama itseisarvo, sattuu Riemannin pallolla samalle "leveyspiirille". Erityisesti jokaista kompleksilukua, jonka itseisarvo on 1, vastaa piste Riemannin pallon "päiväntasaajalla", jossa $\varphi$ = 0. Kompleksitason nollapistettä vastaa Riemannin pallon "etelänapa", jossa $\varphi =-{\frac {\pi }{2}}$, ja äärettömyyspistettä pallon "pohjoisnapa", jossa $\varphi ={\frac {\pi }{2}}$. Mitä suurempi on kompleksiluvun itseisarvo, sitä lähempänä sen vastinpiste Riemannin pallolla on sen pohjoisnapaa.

Kahden projektion etäisyys Riemannin pallon pinnalla

Kahden projektion $Z$ ja $W$, joita vastaavat kompleksiluvut $z$ ja $w$, välistä etäisyyttä merkitään symbolilla $\chi$.. Tämä lasketaan kaavalla $\chi [z,w]:={\frac {2|z-w|}{{\sqrt {1+|z|^{2}}}{\sqrt {1+|w|^{2}}}}}$. $\chi$ on metriikka.

Lähteet

• Saff, Edward B. ja Snider, Arthur David: Fundamentals of Complex Analysis: Engineerging, Science, and Mathematics,Pearson 3. painos