Stereografinen projektio
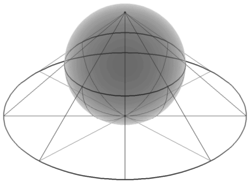
Stereografinen projektio on geometrinen kuvaus, joka kuvaa koko pallopinnan tasolle yhtä pistettä lukuun ottamatta. Tällöin pallopinnalta valitaan yksi kiinteä piste projektiopisteeksi, ja jokaista muuta pallopinnan pistettä vastaa se piste, jossa tämän projektiopisteen ja annetun pisteen kautta kulkeva suora leikkaa tason.
Tämä kuvaus on määritelty kaikissa pallonpinnan pisteissä paitsi projektiopisteessä. Funktio on määrittelyjoukossaan sileä ja bijektio. Se on myös konforminen, koska siinä kulmat pysyvät alkuperäisen suuruisina. Toisaalta se ei kuvaa tarkasti pinta-alaa, varsinkaan projektiopisteen lähellä.
Intuitiivisesti stereografinen funktio on siis tapa kuvata pallopinta tasolle, mitä tosin ei mitenkään voida tehdä niin, että kaikkien pallopinnan alueiden muodot ja koot säilyisivät. Koska pallopinta ja taso esiintyvät monilla matematiikan aloilla, on stereografisella projektiollakin monia erilaisia sovelluksia: sitä käytetään kompleksianalyysissä, karttaprojektiona, geologiassa ja valokuvauksessa. Käytännössä stereografinen projektio voidaan toteuttaa tietokoneella tai käsin erityisellä tavalla ruudutetulla paperilla, jota sanotaan stereografiseksi verkoksi, lyhemmin stereoverkoksi tai Wulffin verkoksi.
Historia[muokkaa | muokkaa wikitekstiä]




Stereografisen funktion tunsivat ainakin jo Hipparkhos ja Ptolemaios, mutta mahdollisesti se tunnettiin Egyptissä jo ennen heitä.[1] Sitä nimitettiin alkujaan planisfääriprojektioksi.[2] Ptolemaioksen teos Planisphaerium on vanhin säilynyt kirjallinen lähde, jossa sitä kuvataan. Sitä käytettiin varsinkin tähtikartoissa.[2] Erästä tähtikarttatyyppiä sanotaan nykyisinkin planisfääriksi.
Stereografista projektiota käytettiin 1500-luvulta lähtien yleisesti myös maapallon kartoissa. Tällöin projektiopisteet olivat päiväntasaajalla. Maapallo jaettiin kahteen pallonpuoliskoon, joiden keskipisteet olivat päiväntasaajalla vastakkaisilla puolilla maapalloa, ja kumpikin kuvattiin tällä projektiolla omalle ympyränmuotoiselle alueelleen. Ensimmäinen tällaisen maailmankartan laati tiettävästi Gualterius Lud vuonna 1507, myöhemmistä vastaavanlaisista kartoista tunnetuimpia ovat Jean Rozen vuonna 1542 ja Rumold Mercatorin vuonna 1595 laatimat.[1] Varsinkin 1600-luvulla projektio oli maailmankartoissa hyvin suosittu.[1][3]
François d'Aguilon antoi stereografiselle projektiolle sen nykyisen nimen vuonna 1613 teoksessaan Opticorum libri sex philosophis juxta ac mathematicis utiles ("Kuusi sekä filosofeille että matemaatikoille hyödyllistä kirjaa optiikasta").[4]
Vuonna 1695 Edmond Halley, jota kiinnosti ennen kaikkea projektion käyttö tähtikartoissa, julkaisi ensimmäisen matemaattisen todistuksen sille, että tämä kuvaus on konforminen.[5] Hän käytti tähän Isaac Newtonin vähän aikaisemmin keksimiä differentiaali- ja integraalilaskennan menetelmiä.
Määritelmä[muokkaa | muokkaa wikitekstiä]

Tässä osiossa käsitellään projektiota yksikköpallon pohjoisnavalta päiväntasaajan kautta tasolle. Projektion muita muotoja käsitellään jäljempänä muissa osioissa.
Kolmiulotteisessa avaruudessa yksikköpallo on niiden pisteiden (x, y, z) joukko, jotka toteuttavat yhtälön . Kuvittelemalla pallo karttapalloksi voidaan pistettä (0,0,1) (tai pistejoukkoa ) sanoa "pohjoisnavaksi". Seuraavassa käytetään pallopinnan muiden pisteiden kuin pohjoisnavan joukolle merkintää M. Taso z = 0 kulkee pallon keskipisteen kautta, ja edellisen rinnastuksen mukaisesti sen ja pallopinnan leikkausta voidaan sanoa "päiväntasaajaksi" eli "ekvaattoriksi". Vastaavalla tavalla käytetään jäljempänä muitakin maantieteellisiä termejä kuten pohjoinen ja eteläinen pallonpuolisko, leveyspiiri ja pituuspiiri eli meridiaani.
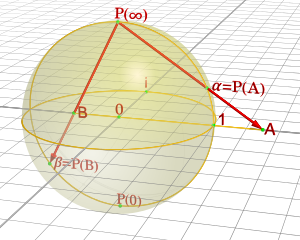
Jokaista M:n pistettä O kohti on yksi ja vain yksi suora, joka kulkee navan N ja pisteen P kautta, ja se leikkaa päiväntasaajatason x = 0 yhdessä ja vain yhdessä pisteessä P′. Tämä piste määritellään pisteen P stereografiseksi projektioksi kyseisellä tasolla.[6]
Kun pallopinnan pisteille käytetään karteesisia koordinaatteja (x, y, z) ja tason pisteelle koordinaatteja (X, Y), projektio ja sen käänteiskuvaus voidaan esittää yhtälöillä:
Kun pallopinnalla käytetään pallokoordinaatteja (φ, θ) (missä φ on leveyspiiri tai atsimuutti, 0 ≤ φ ≤ π) ja θ pituuspiiri tai zeniittikulma, 0 ≤ θ ≤ 2π) ja tasolla napakoordinaatteja (R, Θ), projektio ja sen käänteiskuvaus ovat:
(Pallopinnalla zeniittikulma ja atsimuutti merkitsevät oleellisesti samaa kuin leveys- ja pituuspiiri maapallolla, mutta kulmayksikkönä käytetään tässä radiaania, ei astetta. Lisäksi zeniittikulma luetaan etelänavalta, ei päiväntasaajalta mitattuna.)
Tässä φ:n käsitetään saavan arvo π, kun R = 0. Trigonometristen funktioiden muunnoskaavojen avulla nämä yhtälöt voidaan kirjoittaa moneen muuhunkin muotoon. Jos pallopinnalla käytetään sylinterikoordinaatteja (r, θ, z) ja tasolla napakoordinaatteja (R, Θ), projektio ja sen käänteiskuvaus ovat:
Ominaisuuksia[muokkaa | muokkaa wikitekstiä]
Edellä määritellyssä stereografisessa projektiossa yksikköpallon "etelänapa" (0, 0 −1) kuvautuu tason origoon (0, 0), päiväntasaaja yksikköympyrälle, eteläinen pallonpuolisko ympyrän sisäpuolelle ja pohjoinen pallonpuolisko sen ulkopuolelle.
Projektio ei ole määritelty projektiopisteessä N = (0, 0, 1). Tämän pisteen pienet ympäristöt kuvautuvat tasoalueille, jotka ovat kaukana origosta (0, 0). Mitä lähempänä piste P on projektiopistettä (0, 0, 1), sitä kauempana sen kuvapiste on tason pisteestä (0, 0). Tästä syystä on tapana sanoa, että piste (0, 0, 1) kuvautuu tasolla "äärettömyyteen" ja että taso voidaan täydentää pallopinnaksi lisäämällä siihen yksi "äärettömän kaukainen piste". Tämä ajattelutapa on osoittautunut käyttökelpoiseksi projektiivisessa geometriassa ja kompleksianalyysissä. Topologisella tasolla se osoittaa, että pallopinta on homeorfinen tason yhden kompaktisoinnin kanssa.
Karteesisissa koordinaateissa pallopinnan piste P(x, y, z) ja sen tasolla oleva kuvapiste P′(X, Y) ovat joko molemmat rationaalipisteitä tai kumpikaan ei ole:


Stereografinen projektio on konformikuvaus, mikä merkitsee, että siinä kulmat, joissa käyrät leikkaavat toisensa, säilyvät ennallaan, kuten oheiset kuviot osoittavat. Sitä vastoin pinta-alat eivät säily: yleensä alueen pinta-ala pallopinnalla ei ole yhtä suuri kuin sitä vastaavan alueen pinta-ala tasolla. Pinta-ala-alkio X,Y -koordinaateissa on:
Ainoastaan yksikköympyrän kohdalla infinitesimaalisten alueiden pinta-ala säilyy. Origon (0,0) välittömässä läheisyydessä olevien pienten alueiden pinta-ala on tasolla vain neljäsosa siitä, mikä se on pallopinnalla, ja kaukana origosta pinta-alamittakaava lähestyy ääretöntä.
Metriikka (X, Y) -koordinaateissa on:
- ,
mikä on ainoa Bernhard Riemannin geometrian perusteita käsittelevässä, Göttingenissä vuonna 1854 julkaistussa artikkelissa Über die Hypothesen welche der Geometrie zu Grunde liegen esiintyvä matemaattinen kaava.
Mikään kuvaus pallopinnalta tasolle ei voi olla sekä konforminen että säilyttää myös pinta-alat, Jos säilyttävä. Jos sellainen kuvaus olisi olemassa, se olisi lokaalinen isometria ja siinä säilyisi myös Gaussin kaarevuus. Kun pallopinnalla ja tasolla kuitenkin on erilainen Gaussin kaarevuus, tämä on mahdotonta.
Stereografisen projektion konformisuudesta seuraa joukko mielenkiintoisia geometrisia ominaisuuksia. Pallopinnan ympyrät, jotka eivät kulje projektiopisteen kautta, kuvautuvat tasolla ympyröiksi. Pallopinnan ympyrät, jotka kulkevat projektiopisteen kautta, kuvautuvat sen sijaan suoriksi. Tämän vuoksi suoria sanotaankin joskus "äärettömyyspisteen kautta kulkeviksi ympyröiksi" tai "ääretönsäteisiksi ympyröiksi".
Stereografisen projektion käänteiskuvauksessa kaikki tason suorat kuvautuvat pallopinnalle projektiopisteen eli äärettömyyspisteen kautta kulkeviksi ympyröiksi. Yhdensuuntaiset suorat, jotka eivät leikkaa toisiaan, kuvautuvat pallopinnalle ympyröiksi, jotka sivuavat toisiaan kyseisessä pisteessä. Niinpä tason kaikkien suorien vastineet pallopinnalla kohtaavat toisensa jossakin; joko ne leikkaavat toisensa kahdessa pisteessä tai ne sivuavat toisiaan projektiopisteessä. (Hieman samantapaisia huomioita voitaisiin tehdä reaalisesta projektiivisesta tasosta, mutta siinä suorien leikkausominaisuudet ovat toisenlaisia.)
Pallopinnan loksodromit kuvautuvat tasolle käyriksi, joiden yhtälö on muotoa
missä parametri a on loksodromin "tiiviys". Toisin sanoen loksodromit kuvautuvat logaritmisiksi spiraaleiksi. Tällainen spiraali leikkaa origon kautta kulkevat säteittäiset suorat kaikkialla yhtä suurissa kulmissa, samoin kuin pallopinnalla loksodromi leikkaa meridiaanit kaikkialla yhtä suurissa kulmissa.

Stereografinen prjektio liittyy tason inversioon yksinkertaisella tavalla. Olkoot P ja Q kaksi pallopinnan pistettä ja P′ ja Q′ niiden kuvapisteet tasolla. Silloin P′ ja Q′ ovat toistensa kuvapisteet tason inversiossa yksikköympyrän suhteen, jos ja vain jos P ja Q ovat toistensa peilikuvat ekvaattoritason suhteen.
Toisin sanoen jos :
- P on pallopinnan piste, ei kuitenkaan pohjoisnapa N eikä sen antipodi eli etelänapa S,
- P′ on P:n kuvapiste stereografisessa projektiossa, jonka projektiopiste on P ja
- P″ on P:n kuvapiste stereografisessa projektiossa, jonka projektiopiste on N,
niin P′ ja P″ ovat toistensa kuvapisteet inversiossa yksikköympyrän suhteen.
Wulffin verkko[muokkaa | muokkaa wikitekstiä]

Stereografisen projektion mukaisia kaavioita voidaan tulostaa tietokoneella käyttämällä edellä esitettyjä kaavoja. Jos niitä kuitenkin on piirrettävä käsin, nämä kaavat ovat hankalia. Sen sijaan käytetään yleisesti tarkoitukseen suunniteltua kuvioitua paperia. Tällaisella viivaverkolla varustettua paperia sanotaan stereoverkoksi tai Wulffin verkoksi, venäläisen mineralogi George Wulffin (Juri Viktorovich) mukaan.[7] Wulffin verkko saadaan aikaan piirtämällä pallonpuoliskolle leveys- ja pituuspiirien verkko ja projisoimalla nämä käyrät sitten levylle.
Kaaviossa se seikka, että stereografinen projektio vääristää pinta-aloja, näkyy vertaamalla lähellä keskipistettä olevaa verkon sektoria reunojen läheisyydessä oleviin. Sektorien pinta-ala pallopinnalla on sama. Tasolla reunassa olevan sektorin pinta-ala on lähes neljä kertaa niin suuri kuin keskellä olevan. Jos verkon tiheyttä suurennetaan, tämä suhde lähestyy arvoa 4.
Wulffin verkossa leveys- ja pituuspiirit leikkaavat toisensa kohtisuorasti. Tämä on suora seuraus stereografisen projektion konformisuudesta. (Tosin konformisuus on vahvempi ominaisuus kuin leveys- ja pituuspiirien kohtisuoruuden säilyminen. On olemassa sellaisiakin kuvauksia pallopinnalta tasolle, joissa leveys- ja pituuspiirit leikkaavat toisensa kohtisuorasti, mutta muut kulmat eivät pysy muuttumattomina; sellaisia ovat esimerkiksi neliökartta ja Gall-Petersin projektio.)

Esimerkkinä Wulffin verkon käytöstä voidaan kuvitella kaksi päällekkäin asetettua ohutta, läpikuultavaa paperia, joista kumpaankin se on kopioitu ja jotka molemmat on suunnattu ja kiinnitetty keskipisteidensä mukaan. Olkoon P pallopinnan piste, jonka pallokoordinaatit ovat (140°, 60°) ja karteesiset koordinaatit näin ollen (0.321, 0.557, −0.766). Tämä piste sijaitsee 60°:n kulmassa vastapäivään positiivisesta x-akselista (tai 30°:n kulmassa myötäpäivään y-akselista) ja origosta katsottuna 50°;n kulmassa vaakatasoon z = 0 nähden. Kun nämä kulmat tunnetaan, P:n asettamiseksi paikoilleen tarvitaan neljä vaihetta:
- Käyttämällä verkoston viivoja, jotka tässä kuviossa ovat 10°:n päässä toisistaan, tehdään merkki siihen leikkauspisteeseen,
joka on 60° vastapäivään pisteestä (1, 0) (tai 30° myötäpäivään pisteestä (0, 1)).
- Kierretään ylempää paperia origon ympäri, kunnes tämä piste on x-akselilla eli samalla suoralla kuin piste (1, 0) alemmalla paperilla.
- Alempaan paperiin painetun verkon avulla merkitään piste, joka on tästä pisteestä 50°:n verran lähempänä keskipistettä.
- Kierretään ylempää paperia päinvastaiseen suuntaan kuin vaiheessa 2, jolloin se on jälleen
kohdallaan alempaan paperiin painetun verkon kanssa. Vaiheessa 3 merkitty piste päätyy tällöin haluttuun projektiopisteeseen. Muiden pisteiden kuvaamiseksi, joiden kulmat eivät ole sellaisia pyöreitä lukuja kuin 60° ja 50°, on suoritettava visuaalinen interpolaatio verkoston lähimpien viivojen väliin. Tämä käy helpommin, jos verkon viivat ovat tiheämmässä kuin 10°:n välein. Usein ne painetaan 2°:n välein.
Kahden pallopinnalla olevan pisteen stereografisten kuvapisteiden välinen keskuskulma voidaan määrittää merkitsemällä niiden vastinpisteet Wulffin verkkoon, jota sitten kierretään keskipisteensä ympäri, kunnes pisteet ovat meridiaanilla tai lähellä sitä. Sen jälkeen niiden välinen kulma voidaan mitata laskemalla verkoston viivat, jotka leikkaavat tämän meridiaanin.
-
Kais pistettä P1 ja P2 piirrettyinä läpikuultaville papereille, joihin on merkitty Wulffin verkosto ja jotka on kiinnitetty toisiinsa origossa.
-
Läpikuultava lehti kierrettynä origon ympärille, jolloin pisteiden P1 ja P2 välinen keskuskulma näkyy molempien kautta kulkevalta meridiaanilta.
Muita muotoiluja ja yleistyksiä[muokkaa | muokkaa wikitekstiä]

Eri lähteissä on stereografinen projektio määritelty hieman eri tavoin. Toisinaan stereografinen projektio pohjoisnavalta (0, 0, 1) määritellään kuvaukseksi tasolle z = -1, joka sivuaa yksikköpalloa etelänavalla eli pisteessä (0, 0, -1).[8] Tällaisessa projektiossa saadut arvot X ja Y ovat aina tasan kaksi kertaa niin suuret kuin edellä kuvatussa projektiosa ekvaattoritasolle. Esimerkiksi tässä projektiossa päiväntasaajaa vastaa ympyrä, jonka keskipiste on origossa ja jonka säde on 2. Sen sijaan että edellä kuvatussa projektiossa pienten alueiden pinta-alat kuvautuvat oikein lähellä päiväntasaajaa, tällaisessa projektiossa ne kuvautuvat oikein etelänavan välittömässä läheisyydessä.
Toisinaan taas projektio muodostetaan pallopinnalta, jonka säde on 1/2, tasolle z = -1/2 [9] tai pallopinnalta, joka sivuaa tasoa origossa ja jonka halkaisija on 1, tasolle z = 0.[10] Siinä tapauksessa kaavat saavat muodon

Yleisesti stereografinen projektio voidaan määritellä mistä tahansa pallopinnan pisteestä Q mille tahansa tasolle E, joka täyttää seuraavat ehdot:
- E on kohtisuorassa pisteen Q kautta kulkevaan pallon halkaisijaan nähden, ja
- piste Q ei ole tasossa E.
Kunhan taso E täyttää nämä ehdot, jokaista pallopinnan pistettä P, pistettä Q lukuun ottamatta, vastaa tasolla yksikäsitteisesti määrätty piste P′, joka määritellään pisteen P stereografiseksi projektioksi tasolla E.[11]
Kaikilla tällä tavoin muodostetuilla stereografisen projektion muotoiluilla on oleellisesti samat ominaisuudet. Ne ovat sileitä bijektioita, diffeomorfismeja, jotka on määritelty kaikkialla paitsi projektiopisteessä. Ne ovat konformisia, eivätkä pinta-alat niissä säily.
Vielä yleisemmin stereografinen projektio voidaan määritellä n-pallolla Sn n+1 -ulotteisessa euklidisessa avaruudessa En+1. Jos Q on Sn:n piste ja E hypertaso avaruudessa En+1, pisteen P ∈ Sn − {Q} stereografinen projektio on suoran ja hypertason E leikkauspiste. Karteesisissa koordinaateissa (pallopinnalla , tasolla ) pisteen projektio Q:sta katsottuna on
- missä 1 ≤ i ≤ 'n.
Määrittelemällä , saadaan käänteiskuvaukseksi
- ja missä 1 ≤ i ≤ 'n.
Vielä yleisemmässä tapauksessa oletetaan, että S on (ei-singulaarinen) toisen asteen hyperpinta projektiivisessa avaruudessa Pn+1. Toisin sanoen S on ei-singulaarisen toisen asteen muodon f(x0, ..., xn+1) nollakohtien ura homogeenisissa koordinaateissa xi. Kiinnitetään hyperpinnalta S jokin valittu piste Q ja valitaan avaruudesta Pn+1 hypertaso E, johon Q ei sisälly. Tällöin pisteen P ∈ S - {Q} stereografinen projektio on :n ja E:n ainoa leikkauspiste. Kuten edellä, stereografinen projektio on konforminen, ja "pienen" joukon ulkopuolella sillä on käänteiskuvaus. Stereografinen projektio esittää toisen asteen hyperpinnan hyperpinnan rationaalisena hyperpintana.[12] Tällä konstruktiolla on merkitystä algebrallisessa geometriassa ja konformissa geometriassa.
Sovelluksia matematiikassa[muokkaa | muokkaa wikitekstiä]
Kompleksianalyysi[muokkaa | muokkaa wikitekstiä]
Vaikka pallopinnalla on yksi piste, projektiopiste, jossa stereografinen projektio ei ole määritelty, koko pallopinta voidaan kuvata käyttämällä kahta projektiota eri projektiopisteistä. Toisin sanoen pallopinta voidaan peittää kahdella tasosta saadulla parametroinnilla, jotka saadaan projektioiden käänteiskuvauksista. Parametroinnit voidaan valita niin, että indusoivat pallopinnalle saman suunnistuksen. Yhdessä ne osoittavat, että pallopinta on suunnistuva pinta ja samalla kaksiulotteinen monisto.
Tällä konstruktiolla on huomattava merkitys kompleksianalyysissa. Tason piste (X, Y), missä X ja Y ovat reaalilukuja, voidaan samastaa kompleksiluvun ζ = X + iY kanssa. Stereografinen projektio pohjoisnavalta päiväntasaajan tasolle on tällöin:
Samoin jos ξ = X − iY on toinen kompleksinen koordinaatti, funktiot
määrittelevät stereografisen projektion etelänavalta päiväntasaajan tasolle. Muunnoskuvaukset, joilla siirrytään ζ-koordinaateista ξ-koordinaatteihin ovat tällöin ja , joista ζ lähestyy nollaa kun ξ lähestyy ääretöntä ja päin vastoin.
Tämä tekee mahdolliseksi lisätä kompleksitasoon luonnollisella tavalla äärettömyyspiste . Näin saadaan niin sanottu laajennettu taso . Toisin kuin tavallinen kompleksitaso, laajennettu taso on topologisena avaruutena kompakti.[10] Laajennetun tason jokaista pistettä vastaa kääntäen yksikäsitteisesti piste pallopinnalla, Riemannin pallolla, kun tämä pallo pohjoisnapaa lukuun ottamatta kuvataan stereografisella projektiolla kompleksitasolle ja pohjoisnavan kuvapisteeksi määritellään piste .[10] Tämä kuvaus on homeomorfismi. Tähän konstruktioon perustuu koko meromorfifunktioiden teoria. Riemannin pallolle voidaan määritellä myös luonnollinen metriikka, pallometriikka eli Riemannin metriikka, joka määrittää myös sen ja samalla laajennetun tason topologian.[10]
Suorien ja tasojen havainnollistus[muokkaa | muokkaa wikitekstiä]

Kaikki kolmiulotteisen avaruuden origon kautta kulkevat suorat muodostavat avaruuden, jota sanotaan reaaliseksi projektiiviseksi tasoksi. Tätä avaruutta on vaikea havainnollistaa, koska sitä ei voi upottaa kolmiulotteiseen avaruuteen.
Kuitenkin se voidaan "melkein" havainnollistaa levyllä seuraavaan tapaan. Jokainen origon kautta kulkeva suora leikkaa eteläisen pallonpuoliskon z ≤ 0 pisteessä, joka voidaan stereografisesti projisoida levylle. Vaakasuorat viivat leikkaavat pallopinnan kahdessa pisteessä päiväntasaajalla, joista kumpi tahansa voidaan projisoida tasolle; on ymmärrettävä, että vastakkaiset sivut levyn reunalla esittävät samaa suoraa. Kyseessä on tekijätopologia. Niinpä jokainen origon kautta kulkevien suorien joukko voidaan melkein täydellisesti kuvata pistejoukolle levyllä.
Samoin jokainen origon kautta kulkeva taso leikkaa yksikkökiekon jotakin isoympyrää myöten, jota sanotaan tason jäljeksi. Tämä ympyrä voidaan kuvata kiekon ympyrälle stereografisella projektiolla. Näin tämä projektio tekee mahdolliseksi esittää tasoja ympyränkaarina levyllä. Ennen kuin tietokoneita oli käytettävissä, isoympyröiden stereografinen projektio johti usein suurisäteisten kaarien piirtämiseen, mihin tarvittiin erityistä piirustusvälinettä. Nykyisin tämä voidaan suorittaa tietokoneen avulla paljon helpommin.
Jokaiseen tasoon liittyy myös yksikäsitteinen suora, tason napa, joka kulkee origon kautta ja on kohtisuorassa tasoa vastaan. Tätä suoraa vastaa piste levyllä samoin kuin jokaista origon kautta kulkevaa suoraa. Niinpä stereografisella projektiolla voidaan myös havainnollistaa tasoja levyn pisteinä. Kun on kuvattavana useita tasoja, niiden napojen kuvaaminen johtaa vähemmän sekavaan kuvaan kuin niiden jälkien kuvaaminen.
Tätä konstruktiota käytetään kristallografiassa ja geologiassa usein suuntatietojen havainnollistamiseen jäljempänä kuvatulla tavalla.
Muita havainnollistuksia[muokkaa | muokkaa wikitekstiä]
Stereografista projektiota käytetään myös polytooppien havainnollistamiseen. Schlegelin diagrammisa avaruuden n-ulotteinen polytooppi projisoidaan n-ulotteiselle pallolle, joka sen jälkeen projisoidaan stereografisesti avaruudelle . Kutistaminen :sta :ään voi tehdä polytoopin helpommaksi havainnollistaa ja ymmärtää.
Aritmeettinen geometria[muokkaa | muokkaa wikitekstiä]

Alkeellisessa aritmeettisessa geometriassa yksikköympyrän stereografinen projektio tarjoaa keinon löytää kaikki Pythagoraan kolmikot. Ympyrän stereografisessa projektiossa pohjoisnavalta (0,1) x-akselille jokaista sellaista yksikköympyrän pistettä (x, y), jossa molemmat koordinaatit ovat rationaalilukuja, vastaa kääntäen yksikäsitteisesti jokin rationaaliluku x-akselilla. Jos on x-akselin rationaalipiste, sen käänteinen stereografinen projektio yksikköympyrällä on
missä osoittajat n2-m2 ja 2mn sekä yhteinen nimittäjä n2+m2 muodostavat Pythagoraan kolmikon.
Tangentin puolikulmamuunnos[muokkaa | muokkaa wikitekstiä]

Trigonometristen funktioiden pari (sin x, cos x) muodostaa yksikköympyrän erään parametriesityksen. Stereografisen projektion avulla sille voidaan muodostaa toinenkin parametriesitys:
Tällä parametrisaatiolla pituusalkio yksikköympyrän pituusalkio dx saadaan muotoon
Alkion dx korvaaminen tällä lausekkeella yksinkertaistaa toisinaan trigonometrisia funktioita sisältävien lausekkeiden integrointia.
Sovelluksia muilla aloilla[muokkaa | muokkaa wikitekstiä]
Stereografinen projektio karttaprojektiona[muokkaa | muokkaa wikitekstiä]


Kartografian perusongelma on, että kuvattiinpa pallopinta tasolle millä tavalla tahansa, eivät kartassa voi sekä kulmat (ja näin ollen alueiden muodot) että pinta-alojen suhteet näkyä oikein. On kuitenkin olemassa karttaprojektioita, joissa pinta-alojen suhteet ovat oikein, ja toisia, joissa kulmat ovat oikein. Edelliset soveltuvat varsinkin tilastollisiin karttoihin, jälkimmäisiä navigointiin.
Stereografinen projektio kuuluu jälkimmäiseen luokkaan. Jos projektion keskukseksi valitaan pohjois- tai etelänapa, sillä on lisäetuna, että kaikki pituuspiirit näkyvät navasta lähtevinä suorina viivoina, kaikki leveyspiiri taas napaa ympäröivinä samankeskeisinä ympyröinä. Nykyään tätä projektiota käytetäänkin ennen kaikkea napaseutujen kartoissa.[1]
Stereografisessa projektiossa kaikki pallopinnan ympyrät kuvautuvat ympyröiksi paitsi projektiopisteen kautta kulkevat suoriksi. Tämän vuoksi se soveltuu myös Kuun ja vieraiden planeettojen karttoihin, joissa kraatterit ovat tyypillisiä piirteitä. USGS onkin käyttänyt tätä projektiota Kuun, Merkuriuksen ja Marsin kartoissa.[1]
Kristallografia[muokkaa | muokkaa wikitekstiä]
| Tämän artikkelin tai sen osan paikkansapitävyys on kyseenalaistettu. Voit auttaa varmistamaan, että kyseenalaistetut väittämät ovat luotettavasti lähteistettyjä. Lisää tietoa saattaa olla keskustelusivulla. Tarkennus: Onko tämä osio käännetty oikein? (Osio Chrystallography engl. Wikipedian artikkelissa en:Stereographic projection.) |

Kristallografiassa kiteiden akselien ja sivujen suuntautuminen kolmiulotteisessa avaruudessa on keskeinen geometrinen tutkimuskohde, joka voidaan selvittää tulkitsemalla esimerkiksi röntgensäteilyn ja elektronien diffraktiokuvioita. Nämä suuntautumiset voidaan havainnollistaa niin kuin edellä on kerrottu osiossa Suorien ja tasojen havainnollistus. Toisin sanoen kiteen akselit ja kidetasojen navat leikkaavat pohjoisella pallonpuoliskolla, josta ne sitten kuvataan tasolle stereografisella projektiolla. Napoja esittävää kaaviota sanotaan napakuvioksi (engl. pole figure).
Elektronidiffraktiossa Kikuchin viivaparit näkyvät nauhoina hilatason jälkien ja Ewaldin pallon leikkausviivan ympärillä ja täten ne tarjoavat kokeellisen pääsyn kiteen stereografiseen projektioon. Kikuchin kaavioiden mallit käänteisavaruudessa[13] ja taivutettujen ääriviivojen kanssa käytettävät reunaviivojen kaaviot suorassa avaruudessa[14] toimivat täten tiekarttoina, joiden avulla saadaan tietoa kiteiden suuntautumisesta transmissioelektronimikroskoopissa.
| Tämä artikkeli tai sen osa on tuotu vieraskielisestä lähteestä ja käännös on keskeneräinen. Voit auttaa Wikipediaa tekemällä käännöksen loppuun. |
Valokuvaus[muokkaa | muokkaa wikitekstiä]

Jotkin kalansilmälinssit käyttävät stereografista projektiota ottaakseen laajakulmaisia näkymiä.[15] Verrattuna vanhemman tyyppisiin kalansilmälinsseihin, joissa käytetään oikeapintaista projektiota, lähellä reunoja olevat alueet säilyttävät muotonsa ja suorat viivat kaareutuvat vähemmän. Steregrafiset kalansilmälinssit ovat yleenä kuitenkin kalliimpia valmistaa.[16] Kuvien uudelleenmuotoiluun tarkoitetuilla ohjelmilla kuten Panotools voidaan myös oikeapintaisella kalansilmällä otetut kuvat automaattisesti muuntaa stereografiseen projektioon.
Stereografista projektiota on käytetty pallomaisten näkymien kuvaamiseen. Tämä johtaa ilmiöihin, joita sanotaan pieneksi planeetaksi (kun projektion keskus on nadiirissa) tai putkeksi (kun projektion keskus on zenitissä).[17]
Sen, että stereografista projektiota käytetään näkymien kuvaamiseen enemmän kuin muita tasoprojektioita, katsotaan johtuvan siitä, että projektion konformisuuden vuoksi siinä muodot säilyvät.[17]
Katso myös[muokkaa | muokkaa wikitekstiä]
Lähteet[muokkaa | muokkaa wikitekstiä]
- James Brown, Ruel Churchill: Complex variables and applications. New York: McGraw-Hill, 1989. ISBN 0-07-010905-2.
- Feature column February 2014: Stereographic Projection 2014. Bill Casselman, AMS.
- Manfredo P. Do Carmo, Manfredo P.: Differential geometry of curves and surfaces. Prentice Hall: Englewood Cliffs, 1976. ISBN 0-13-212589-7.
- John Oprea: Differential geometry and applications. Englewood Cliffs, New Jersey: Prentice Hall, 2003. ISBN 0-13-065246-6.
- John P. Snyder: An Album of Map Projections, Professional Paper 1453. US Geological Survey, 1989.
- Michael Spivak: A comprehensive introduction to differential geometry, Volume IV. Houston, Texas: Publish or Perish, 1999. ISBN 0-914098-73-X.
Viitteet[muokkaa | muokkaa wikitekstiä]
- ↑ a b c d e John P. Snyder: Map Projections − A Working Manual, Professional Paper 1395, s. 154–160. US Geological Survey, 1987. Teoksen verkkoversio. (Arkistoitu – Internet Archive)
- ↑ a b John P. Snyder: Flattening the Earth. University of Chicago, 1993. ISBN 0-226-76746-9.
- ↑ Lloyd Arnold Brown: The story of maps, s. 59. Courier Corporation, 1979. Teoksen verkkoversio.
- ↑ James Elkins: Did Leonardo Develop a Theory of Curvilinear Perspective?: Together with Some Remarks on the 'Angle' and 'Distance' Axioms. (Lainaus Ekertin teoksesta "Die Kartenwissenschaft", Berliini 1921, sivut 121–123) Journal of the Warburg and Courtauld Institutes, 1988, 51. vsk, s. 190–196. doi:10.2307/751275. JSTOR 751275.
- ↑ Timothy Feeman: Portraits of the Earth: A Mathematician Looks at Maps. American Mathematical Society, 2002.
- ↑ Olli Lehto: ”Pintojen teoriaa”, Differentiaali- ja integraalilaskenta II, s. 33. Offset Oy, 1978.
- ↑ George Wulff: Untersuchungen im Gebiete der optischen Eigenschaften isomorpher Kristalle:. Zeits. Krist, 1902, nro 36, s. 1–28.
- ↑ Tom Apostol: Mathematical Analysis (2. painos). Addison-Wesley, 1974. ISBN 0-201-00288-4.
- ↑ I. M. Gelfand, R. A. Minlos, Z Ya Shapiro: Representations of the Rotation and Lorentz Groups and their Applications. New York: Pergamon Press, 1963.
- ↑ a b c d Olli Lehto: ”Laajennettu taso”, Funktioteoria I–II, s. 11–12. Limes ry, 1980. ISBN 951-745-077-X.
- ↑ Dan Pedoe: Geometry. Dover, 1988. ISBN 0-486-65812-0.
- ↑ Igor Shafarevich: Basic Algebraic Geometry I. Springer, 1995. ISBN ISBN 0-387-54812-2.
- ↑ M. von Heimendahl, W. Bell, G. Thomas: Applications of Kikuchi line analyses in electron microscopy. J. Appl. Phys, 1964, 35. vsk, nro 12, s. 3614–3616.
- ↑ P. Fraundorf, Wentao Qin, P. Moeck, Eric Mandell: Making sense of nanocrystal lattice fringes. J. Appl. Phys, 2005, 98. vsk, nro 114308.
- ↑ Samyang 8 mm f/3.5 Fisheye CS syopt.co.kr. Arkistoitu 29.6.2011. Viitattu 4.2.2016.
- ↑ Samyang 8 mm f/3.5 Aspherical IF MC Fish-eye lenstip.com. Viitattu 4.2.2016.
- ↑ a b Daniel German, L. Burchill, A. Duret-Lutz, S. Pérez-Duarte, E. Pérez-Duarte, J. Sommers: Flattening the Viewable Sphere. (Banffissa pidetyn konferenssin julkaisu) Proceedings of Computational Aesthetics, kesäkuu 2007, s. 23–28. Eurographics.
Aiheesta muualla[muokkaa | muokkaa wikitekstiä]
- Eric W. Weisstein: Stereographic Projection Wolfram MathWorld.
- Stereographic Projection PlanetMath. Arkistoitu 10.3.2013. Viitattu 4.2.2016.
- Alexander Bogomolny: Stereographic Projection and Inversion Cut-the-Knot.
- DoITPoMS TLP Library: The Stereographic Projection Cambridgen yliopisto.
Videoita[muokkaa | muokkaa wikitekstiä]
- Proof about Stereographic Projection taking circles in the sphere to circles in the plane isallaboutmath.com.
- Stereographic Projection Time Laps vimeo.com.
Ohjelmisto[muokkaa | muokkaa wikitekstiä]
- transformation-crystallography-lab code.google.com.
- Stereographic Projection Demo (Java-applet) torus.math.uiuc.edu. Arkistoitu 26.1.2021. Viitattu 4.2.2016.
Miniplaneettapanoraamoja[muokkaa | muokkaa wikitekstiä]
- Miniplaneettapanoraamoja pääasiassa Britanniasta miniplanets.co.uk. Arkistoitu 8.7.2010. Viitattu 4.2.2016.
- Miniplaneettapanoraamoja pääasiassa Tšekistä miniplanet.net.
- Miniplaneettapanoraamoja pääasiassa Puolasta panoramy.zbooy.pl. Arkistoitu 18.4.2021. Viitattu 4.2.2016.










































