Kategoriateoria

Kategoriateoria on matematiikan osa-alue, joka tutkii matemaattisia rakenteita keskittymällä objektien välisiin suhteisiin ja yhteyksiin. Kategoriateorian peruskäsite on kategoria, jonka voidaan ajatella olevan tietty matemaattinen konteksti, jossa käsillä olevan matemaattisen teorian diskurssi tapahtuu. Kategorioita tavataan lähes kaikilla matematiikan osa-alueilla, joten kategoriateoreettisia käsitteitä ja tuloksia voidaan käyttää matemaattisten teorioiden jäsentelyyn ja tutkimiseen. Kategorioita voidaan kuitenkin tutkia myös itsenäisinä olioina, ilman suoraa yhteyttä muihin matematiikan osa-alueisiin.
Kategoriateorian keskiössä ovat niin sanotut universaaliominaisuudet: oliot määritellään suhteessa kaikkiin tietyn kontekstin (eli kategorian) olioiden suhteen.[1] Tällä tavoin määritellyt oliot eivät siis ole olemassa itsenäisesti, vaan oleellisella tavalla riippuvat ja sisältävät informaatiota siitä kontekstista tai teoriasta, johon kuuluvat. Tärkeä kategoriateoreettinen tulos on Yonedan lemma, joka karkeasti ottaen sanoo, että kaikki kategorian objektit määräytyvät yksikäsitteisesti universaaliominaisuuksiensa kautta.[2]
Kategoriateoria syntyi puhtaan matematiikan osa-alueena homologisen algebran tarpeisiin, minkä jälkeen sitä on sovellettu ja kehitetty matematiikan sisällä muun muassa algebrallisen topologian, algebran ja matemaattisen logiikan yhteydessä. Tämän lisäksi kategoriateoriaa on sovellettu matematiikan ulkopuolella muun muassa tietojenkäsittelytieteessä, fysiikassa, teoreettisessa biologiassa, systeemiteoriassa ja kieliteknologiassa.
Historia ja motivaatio[muokkaa | muokkaa wikitekstiä]
Saunders Mac Lane ja Samuel Eilenberg määrittelivät funktorit ja luonnolliset isomorfismit ryhmäteorian kontekstissa artikkelissaan vuodelta 1942. Heidän tarkoituksensa oli homologisessa algebrassa usein esiintyneiden "luonnollisten isomorfismien" systematisointi ja täsmällinen määrittely. Näiden määrittelemistä varten tarvittiin funktorin määritelmä, mikä puolestaan johti heidät esittelemään esimerkkejä luonnollisista muunnoksista muilta matematiikan osa-alueilta heidän seuraavassa artikkelissaan vuodelta 1945. Tässä artikkelissa myös määriteltiin kategoria ensimmäisen kerran.[3]
Kategoriat[muokkaa | muokkaa wikitekstiä]
- Pääartikkeli: Kategoria (matematiikka)
Kategoria on kategoriateorian perusyksikkö, joka koostuu objekteista sekä näiden välisistä morfismeista. Morfismit voidaan ajatella prosesseina, joilla on lähtöpiste tietyssä oliossa (morfismin lähtöobjekti) sekä päätepiste jossakin toisessa oliossa (morfismin maaliobjekti). Morfismien ja objektien määritelmä on kuitenkin täysin formaali eikä edellytä tällaista intuitiota. Kategorian mille tahansa objektille on olemassa identiteettimorfismi, ja mitkä tahansa kaksi peräkkäistä morfismia voidaan yhdistää yhdisteeksi. Lisäksi pätevät identiteettilaki ja liitäntälaki: minkä tahansa morfismin yhdiste identiteettimorfismin kanssa on sama kuin kyseinen morfismi, ja yhdisteen järjestyksellä ei ole väliä (katso kategorian täsmällinen määritelmä).
Yleisiä periaatteita[muokkaa | muokkaa wikitekstiä]
Kommutatiiviset kaaviot[muokkaa | muokkaa wikitekstiä]

Kategoriateorian tunnusomaisin merkintä ja samalla tärkeä todistustekniikka on kommutatiivinen kaavio. Tässä kontekstissa kaavioita (kommutatiivisia tai ei) käytetään yleensä epämuodollisesti, mutta mikä tahansa kaavio voitaisiin periaatteessa esittää muodollisesti kaavion määritelmän avulla.
Kaavio koostuu objekteista, joita merkitään pistein tai kirjaimin, esimerkiksi ja , ja näiden välisistä morfismeista, joita merkitään nuolin, esimerkiksi ja . Kaavio on kommutatiivinen, jos kaikki kaavion morfismit kaavion minkä tahansa kahden objektin välillä (mukaan lukien yhdisteet) ovat yhtä suuria. Toisin sanoen kommutatiivisessa kaaviossa ei ole väliä, mitä "reittiä" (eli morfismien yhdisteitä) yhdestä objektista päädytään toiseen.[4] Yllä olevassa esimerkissä kommutatiivisuus tarkoittaisi, että .
Universaaliominaisuudet ja yksikäsitteisyys isomorfismia vaille[muokkaa | muokkaa wikitekstiä]
Koska kategoriateoria keskittyy objektien (ja morfismien) keskinäisiin suhteisiin, tietty objekti tai morfismi määritellään yleensä suhteessa muihin kategorian objekteihin tai morfismeihin. Tällöin puhutaan objektin tai morfismin universaaliominaisuudesta.[1] Universaaliominaisuuden kautta määriteltyä objektia tai morfismia kutsutaan vastaavasti universaaliobjektiksi tai universaalimorfismiksi.
Esimerkiksi alkuobjekti määritellään universaaliominaisuuden kautta: objekti on alkuobjekti mikäli mille tahansa objektille on olemassa täsmälleen yksi morfismi .
Objekteille (ja morfismeille), jotka on määritelty universaaliominaisuuden kautta, on tyypillistä yksikäsitteisyys, mikäli isomorfisten objektien katsotaan olevan "yhtä suuria" tai "samoja".[5] Täsmällisesti, määritellään objektien yksikäsitteisyys isomorfismia vaille ominaisuuden suhteen seuraavasti: mikäli sekä objektilla että objektilla on ominaisuus , niin on olemassa isomorfismi :sta :hen (eli siis myös isomorfismi :stä :hen). Tätä tiukempi käsite on yksikäsitteisyys yksikäsitteistä isomorfismia vaille, joka määritellään muuten samalla tavalla kuin yksikäsitteisyys isomorfismia vaille, mutta objektien välinen isomorfismi on lisäksi yksikäsitteinen.
Esimerkiksi alkuobjekti, mikäli se on olemassa, on yksikäsitteistä isomorfismia vaille yksikäsitteinen.
Vastakkainen kategoria ja duaalisuus[muokkaa | muokkaa wikitekstiä]
Olkoon kategoria. Tällöin sen vastakkainen kategoria määritellään siten että , ja jokaiselle objektiparille olkoon .[6] Selvästi .
Tärkeä kategoriateoreettinen käsite on duaalisuus: mitä tahansa lausetta tai käsitettä, joka pätee tai on määritelty jossakin kategoriassa, vastaa lause tai käsite vastakkaisessa kategoriassa, jota kutsutaan duaalilauseeksi tai -käsitteeksi.[7] Esimerkiksi yllä mainituista käsitteistä alku- ja loppuobjekti sekä mono- ja epimorfismi ovat toistensa duaalikäsitteitä. Täsmällisesti, erään kategorian objekti on alkuobjekti jos ja vain jos se on loppuobjekti vastakkaisessa kategoriassa, ja morfismi on monomorfismi jos ja vain jos se on epimorfismi vastakkaisessa kategoriassa.
Tietyn käsitteen duaalikäsitteen nimi muodostetaan usein, muttei kuitenkaan aina, lisäämällä kyseisen käsitteen nimen eteen ko-etuliite.
Funktorit[muokkaa | muokkaa wikitekstiä]
Myös kategoriat muodostavat kategorian, jonka morfismeina ovat funktorit.
Olkoot ja kategorioita. Funktori kategoriasta kategoriaan koostuu seuraavista kuvauksista:[8]
- jokaiselle objektille , objekti , ja
- jokaiselle :n morfismille kategorian morfismi ,
jotka lisäksi toteuttavat seuraavat ehdot:
- identiteetin säilytys: jokaiselle objektille pätee , ja
- yhdisteen säilytys: jokaiselle :n morfismiparille ja pätee .
Erityisiä funktoreita[muokkaa | muokkaa wikitekstiä]
Olkoon funktori. Määritellään jokaiselle objektiparille kuvaus siten että . Funktori on
- täysi mikäli jokaiselle objektiparille , kuvaus on surjektio,[9]
- uskollinen mikäli jokaiselle objektiparille , kuvaus on injektio,[9]
- täysin uskollinen mikäli se on sekä täysi että uskollinen,[10]
- oleellisesti surjektio objekteille mikäli jokaiselle objektille on olemassa objekti siten että ja ovat isomorfisia.[11]
Esimerkkejä[muokkaa | muokkaa wikitekstiä]
- Mille tahansa (ei tyhjille) kategorioille ja sekä objektille voidaan määritellä vakiofunktori , jonka arvo kaikilla :n objekteilla on ja kaikilla :n morfismeilla .
Luonnolliset muunnokset[muokkaa | muokkaa wikitekstiä]
Kahden kategorian väliset funktorit voidaan niin ikään järjestää kategoriaksi. Morfismeiksi tarvitaan tällöin luonnolliset muunnokset. Itse asiassa Eilenbergin ja Mac Lanen alkuperäinen motivaatio oli algebrallisessa topologiassa käytettyjen "luonnollisten" kuvausten täsmällinen määritelmä, jota varten he määrittelivät sekä kategoriat että funktorit.
Olkoot funktoreita. Luonnollinen muunnos koostuu :n morfismista jokaiselle :n objektille , siten että jokaiselle :n morfismille pätee . Toisin sanottuna jokaiselle morfismille kaavio
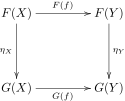
on kommutatiivinen.[12]
Luonnollisesta muunnoksesta käytetään myös suomenkielistä nimeä luonnollinen transformaatio (engl. natural transformation).[13]
Yksittäistä morfismia , joka on osa luonnollista muunnosta, kutsutaan :n komponentiksi, tai täsmällisemmin -komponentiksi.[12]
Luonnollista muunnosta, jonka jokainen komponentti on isomorfismi, kutsutaan luonnolliseksi isomorfismiksi.[14] Luonnolliset isomorfismit ovat isomorfismeja kategoriassa, jonka muodostavat kahden kategorian väliset funktorit sekä näiden väliset luonnolliset muunnokset.
Kategorioiden ekvivalenssi[muokkaa | muokkaa wikitekstiä]
Koska (pienet) kategoriat ja funktorit muodostavat (suuren) kategorian, isomorfismin määritelmä pätee myös funktoreille. Kategorioiden isomorfisuus yhtenevyyden mittana on kuitenkin useissa tilanteissa liian tiukka, sillä se sivuuttaa sen faktan, että kategorioiden kategoriassa jokainen objekti omaa kategorian rakenteen. "Oikeampi", tai ainakin käytännällisempi, yhtenevyyden mitta onkin kategorioiden ekvivalenssi, joka muistuttaa muodoltaan topologisten avaruuksien homotopiaekvivalenssia.
Olkoot ja kategorioita. Tällöin kategorioiden ja ekvivalenssi koostuu seuraavista:
- funktori ,
- funktori ,
- luonnollinen isomorfismi ,
- luonnollinen isomorfismi .[15]
Rajat ja korajat[muokkaa | muokkaa wikitekstiä]

Kaaviot ja kartiot[muokkaa | muokkaa wikitekstiä]
Olkoon pieni kategoria. Tällöin funktoria kutsutaan :n muotoiseksi kaavioksi kategoriassa . Kategoriaa kutsutaan kaavion indeksikategoriaksi.[12]
Kaavion kartio on luonnollinen muunnos . Objektia kutsutaan kartion kärjeksi ja luonnollisen muunnoksen komponentteja kartion särmiksi.[12] Yksityiskohtaisesti kartio koostuu siis objektista ja kokoelmasta morfismeja jokaiseen objektin kuvaan, siten että jokaiselle :n morfismille kaavio

on kommutatiivinen.
Merkitään kartiota, jonka kärki on ja luonnollinen muunnos . Määritellään kartiomorfismi kartiosta kartioon morfismina siten että , jossa on vakio luonnollinen muunnos, jonka jokainen komponentti on .[12] Yksityiskohtaisesti ehto, jonka :n pitää toteuttaa ollakseen kartiomorfismi on: jokaiselle objektille pätee . Jokaisen kaavion kartiot ja kartiomorfismit muodostavat kategorian, jota merkitään ja jota kutsutaan kaavion kartiokategoriaksi.[12]
Rajat[muokkaa | muokkaa wikitekstiä]
Raja voidaan määritellä hyvin lyhyesti kartiokategorian avulla: kaavion raja on kategorian loppuobjekti.[16] Huomataan, että kaikilla kaavioilla ei välttämättä ole rajaa, sillä kartiokategoriassa ei välttämättä ole loppuobjektia. Tästä määritelmästä seuraa, että raja on yksikäsitteistä isomorfismia vaille yksikäsitteinen.
Koska yllä annettu rajan määritelmä on hyvin tiivis, rajan käsitteen merkitys ei välttämättä avaudu siitä. Näin ollen annetaan seuraavaksi yksityiskohtaisempi, mutta yhtäpitävä määritelmä. Olkoon kaavio. Tällöin :n raja koostuu objektista sekä kokoelmasta morfismeja jokaiselle objektille siten että muodostavat kartion (eli jokaiselle :n morfismille alla olevan kaavion sisempi kolmio on kommutatiivinen), ja kartio on lisäksi universaali tämän ominaisuuden suhteen: mikäli on :n objekti ja on morfismi jokaiselle objektille siten että on kartio (eli jokaiselle :n morfismille alla olevan kaavion ulompi kolmio on kommutatiivinen), niin tällöin on olemassa yksikäsitteinen morfismi siten että jokaiselle objektille pätee , eli toisin sanottuna kaavio

on kommutatiivinen.
Kokartiot ja korajat[muokkaa | muokkaa wikitekstiä]
Kaavion kokartio on kaavion kartio, eli luonnollinen muunnos . Samoin kuin kartiolle, objektia kutsutaan kokartion kärjeksi ja komponentteja särmiksi, ja kokartiota merkitään . Kokartiomorfismi kokartiosta kokartioon on morfismi siten että . Merkitään kaavion kokartioiden ja kokartiomorfismien kategoriaa . Tällöin kaavion koraja on kategorian alkuobjekti, mikäli se on olemassa.[17]
Yksityiskohtaisesti, kaavion koraja on kokartio siten että mille tahansa kokartiolle on olemassa yksikäsitteinen morfismi , joka jokaiselle :n morfismille tekee kaaviosta

kommutatiivisen.
Esimerkkejä[muokkaa | muokkaa wikitekstiä]
Esimerkkejä rajoista:
- loppuobjekti on tyhjän kaavion raja,[18]
- binäärinen tulo on sellaisen diskreetin kaavion raja, jossa on täsmälleen kaksi objektia,[20]
- joukkojen ja funktioiden kategoriassa binäärinen tulo on (vailla yksikäsitteistä isomorfismia) kahden joukon karteesinen tulo,[21]
- osittain järjestetyssä joukossa binäärinen tulo on kahden alkion infimum.[20]
Esimerkkejä korajoista:
- alkuobjekti on tyhjän kaavion koraja,[22]
- joukkojen ja funktioiden kategoriassa alkuobjekti (eli tyhjän kaavion koraja) on tyhjä joukko,[19]
- osittain järjestetyssä joukossa alkuobjekti on pienin alkio;[19]
- binäärinen kotulo on sellaisen diskreetin kaavion koraja, jossa on täsmälleen kaksi objektia,[23]
- joukkojen ja funktioiden kategoriassa binäärinen kotulo on (vailla yksikäsitteistä isomorfismia) kahden joukon erillinen yhdiste,[23]
- osittain järjestetyssä joukossa binäärinen kotulo on kahden alkion supremum.[2]
Täydellisyys ja kotäydellisyys[muokkaa | muokkaa wikitekstiä]
Kategorian sanotaan omaavan :n muotoiset (ko)rajat mikäli millä tahansa :n muotoisella kaaviolla on (ko)raja :ssä. Kategoria on (ko)täydellinen mikäli se omaa :n muotoiset (ko)rajat jokaiselle indeksikategorialle .[16] Kategoria on äärellisesti (ko)täydellinen mikäli se omaa :n muotoiset (ko)rajat jokaiselle äärelliselle indeksikategorialle .
Hom-funktorit ja Yonedan lemma[muokkaa | muokkaa wikitekstiä]
Esilyhteet[muokkaa | muokkaa wikitekstiä]
Kategorian esilyhde on funktori . Esilyhteet ja niiden väliset luonnolliset muunnokset muodostavat kategorian, jota merkitään .[24] Mikäli on jonkin topologisen avaruuden avointen joukkojen osittaisjärjestys, niin tämä esilyhteen määritelmä vastaa algebrallisen topologian joukkojen esilyhteen määritelmää.
Hom-funktorit[muokkaa | muokkaa wikitekstiä]
Olkoon lokaalisti pieni kategoria ja olkoon . Määritellään esilyhde seuraavasti: jos ja ovat :n objekteja ja morfismi, niin
- ja ,
jossa on funktio .[25]
Esilyhdettä kutsutaan :n (kontravariantiksi) hom-funktoriksi.[26]
Yonedan upotus[muokkaa | muokkaa wikitekstiä]
Sillä hom-funktori on määritelty mille tahansa lokaalisti pienen kategorian objektille , tämä määrittää kuvauksen
- .
Laajennetaan kyseinen kuvaus funktoriksi
määrittelemällä jokaiselle morfismille luonnollinen muunnos , jonka -komponentti on funktio , joka kuvaa .[27]
Funktoria kutsutaan :n Yonedan upotukseksi.[26] Termin upotus käyttö on perusteltua, sillä yksi Yonedan lemman (ks. alla) seurauksista on Yonedan upotuksen täysi uskollisuus. Näin ollen mikä tahansa lokaalisti pieni kategoria voidaan upottaa sen esilyhteiden kategoriaan; toisin sanottuna on olemassa esilyhteiden kategorian alakategoria, joka on isomorfinen sen kanssa.
Yonedan lemma[muokkaa | muokkaa wikitekstiä]
Hom-funktoreiden erityistä asemaa esilyhteiden kategoriassa kuvastaa Yonedan lemma.
Lause. Olkoon lokaalisti pieni kategoria. Tällöin on olemassa isomorfismi
- ,
joka on luonnollinen sekä objektin että esilyhteen suhteen.[28]
Korollaari. Yonedan upotus on täysi ja uskollinen.[10]
Korollaari. Olkoon lokaalisti pieni kategoria. Tällöin kaikille objekteille pätee:
- jos ja vain jos .[29]
Liittofunktorit[muokkaa | muokkaa wikitekstiä]
Määritelmä morfismijoukkojen isomorfismin kautta[muokkaa | muokkaa wikitekstiä]
Olkoot ja lokaalisti pieniä kategorioita, ja vastakkaisiin suuntiin osoittavien funktoreiden pari. Tällöin sanotaan, että on funktorin vasen liittofunktori (ja vastaavasti on :n oikea liittofunktori) mikäli on olemassa luonnollinen isomorfismi .[10] Isomorfismin luonnollisuus voidaan ilmaista eksplisiittisemmin seuraavasti. Merkitään sekä isomorfismia että sen käänteismorfismia viivalla, eli:
- ja siten että ja .
Tällöin luonnollisuusehto on yhtäpitävä seuraavan ehdon kanssa: kaikille :n morfismeille sekä :n morfismeille pätee
- ja .[30]
Yllä määriteltyä tilannetta merkitään .[10]
Määritelmä yksikön ja koyksikön kautta[muokkaa | muokkaa wikitekstiä]
Oletetaan, että on olemassa luonnollinen muunnos sekä luonnollinen muunnos . Tällöin on liitto mikäli molemmat kaaviot

kommutoivat.
Lause. on liitto jos ja vain jos on :n vasen liittofunktori. Tällöin liitto määrää morfismijoukkojen isomorfismin yksikäsitteisesti, ja käänteisesti, morfismijoukkojen isomorfismi määrää yksikön ja koyksikön yksikäsitteisesti.[31]
Esimerkkejä[muokkaa | muokkaa wikitekstiä]
- Unohdusfunktorilla on sekä vasen että oikea liittofunktorit: , jossa vasen liittofunktori määrittelee jokaiselle joukolle diskreetin topologian, ja oikea liittofunktori indiskreetin topologian.[32]
- Unohdusfunktorilla on vasen liittofunktori, joka määrittelee jokaiselle joukolle sen virittämän vapaan ryhmän.[33]
- Jos ja ovat osittain järjestettyjä joukkoja ja funktoreita (eli järjestyksen säilyttäviä funktioita), niin jos ja vain jos kaikille alkioille ja pätee:
- jos ja vain jos .[34]
- Osittaisjärjestyksen morfismien liitto tunnetaan nimellä Galois'n vastaavuus (tai yhteys).[34]
- Funktorit, jotka muodostavat kategorioiden ekvivalenssin, ovat aina liittofunktoreita.[35]
Sovelluksia[muokkaa | muokkaa wikitekstiä]
Matematiikan ulkopuolella kategoriateoriaa on hyödynnetty eniten teoreettisen tietojenkäsittelytieteen alalla.[36] Esimerkiksi Haskell-ohjelmointikielen voidaan ajatella melkein muodostavan kategorian.[37] Laajemmin ottaen, tarpeeksi abstraktilla tasolla mikä tahansa funktionaalinen ohjelmointikieli voidaan ajatella kategoriana.[38]
Sovellukset pyrkivät usein teorioiden yhdenmukaistamiseen, yksinkertaistamiseen sekä oleellisimpien aspektien esille tuomiseen. Tavoitteena saattaa olla myös informaation, tiedon ja käytänteiden siirron helpottaminen eri alojen välillä.[39][40] Esimerkiksi samoja matemaattisia rakenteita hyödyntäviä kategoriateoreettisia malleja on kehitetty sekä kvanttilaskennan että luonnollisen kielen käsittelyn tarpeisiin.[41]
Monissa sovelluksissa lähtökohtana on monoidaalinen kategoria,[39] eli kategoria , jolle on olemassa funktori , joka toteuttaa tietyt ehdot.[42] Siinä missä tavallinen kategoria sallii prosessien (morfismien) peräkkäisen yhdistämisen, monoidaalinen kategoria sallii tämän lisäksi prosessien yhdistämisen suuremmaksi kokonaisuudeksi, siten että prosesseilla voi olla vaihteleva määrä syöttöjä (lähtöobjekteja) ja tulosteita (engl. output) (maalibjekteja). Esimerkiksi kvanttiteoriasta sekä kemiallisia reaktioita mallintavista Petri-verkoista on kehitetty matemaattisia malleja, jotka hyödyntävät monoidaalisia kategorioita.[43][40]
Biologi Robert Rosen on ehdottanut, että kategoriateorian metodit soveltuvat relaatiobiologian tarpeisiin.[44][45] Osittain Rosenin ajatuksiin perustuen, kategoriateoriaan nojaavaa mallia on ehdotettu biologisten organismien hierarkkisen järjestyksen hahmottamiseen.[46]
Lähteet[muokkaa | muokkaa wikitekstiä]
- Alakoskela, Riina. Epäarkhimediset valuaatiot ja Monskyn lause. Pro gradu -tutkielma. Helsingin yliopisto. Matematiikan ja tilastotieteen laitos. Joulukuu 2020. Viitattu 20.8.2021.
- Barr, Michael & Wells, Charles. Category Theory for Computing Science. Viitattu 20.8.2021. (englanniksi)
- Bradley, Tai-Danae. What is Applied Category Theory? Viitattu 20.8.2021. (englanniksi)
- Coecke, Bob & Sadrzadeh, Mehrnoosh & Clark, Stephen. Mathematical Foundations for a Compositional Distributional Model of Meaning. (englanniksi)
- Ehresmann, Andrée & Vanbremeersch, Jean-Paul. Memory Evolutive Systems; Hierarchy, Emergence, Cognition. Elsevier Science. 2007. ISBN 9780444522443. (englanniksi)
- Fong, Brendan & Spivak, David. Seven Sketches in Compositionality: An Invitation to Applied Category Theory. Viitattu 20.8.2021. (englanniksi)
- Heunen, Chris & Vicary, Jamie. Categories for Quantum Theory. An Introduction. Oxford graduate texts in mathematics 28. Oxford University Press. 2019. ISBN 978-0-19-873961-6. (englanniksi)
- Landry, Elaine & Marquis, Jean-Pierre. Categories in Context: Historical, Foundational, and Philosophical. Philosophia Mathematica. Volume 13. Issue 1. February 2005. Pages 1-43. (englanniksi)
- Leinster, Tom. Basic Category Theory. Cambridge studies in advanced mathematics 143. Cambridge University Press. 2014. ISBN 978-1-107-04424-1. Verkkoversio. (englanniksi)
- Niskanen, Markus. Liittofunktorit. Pro gradu -tutkielma. Tampereen yliopisto. Luonnontieteiden tiedekunta. Matematiikka. Marraskuu 2017. Viitattu 20.8.2021.
- Puuska, Ville. Yleiset persistenssimodulit ja lomitusmetriikat. Pro gradu -tutkielma. Tampereen yliopisto. Informaatiotieteiden yksikkö. Matematiikka. Joulukuu 2016. Viitattu 20.8.2021.
- Riehl, Emily. Category Theory in Context. Dover Publications. 2016. ISBN 978-0-486-80903-8. Verkkoversio. (englanniksi)
- Rosen, Robert. The Representation of Biological Systems from the Standpoint of the Theory of Categories. Bulletin of Mathematical Biophysics 20 (4): 317-341. 1958. DOI 10.1007/bf02477890. (englanniksi)
- Tuomi, Ilkka. Robert Rosenin ennakoivat systeemit ja tieteiden seuraava vallankumous[vanhentunut linkki] Futura 36 (2017) : 3, s. 93-102.
Viitteet[muokkaa | muokkaa wikitekstiä]
- ↑ a b Leinster, Introduction
- ↑ a b Riehl, Preface
- ↑ Landry & Marquis
- ↑ Niskanen, s. 20-21
- ↑ Niskanen, s. 46
- ↑ Niskanen, s. 18
- ↑ Niskanen, s. 18-19
- ↑ Leinster, s. 17
- ↑ a b Leinster, s. 25
- ↑ a b c d Niskanen, s. 41
- ↑ Leinster, s. 34
- ↑ a b c d e f Niskanen, s. 10
- ↑ Niskanen, s. 30
- ↑ Niskanen, s. 31
- ↑ Niskanen, s. 43
- ↑ a b Niskanen, s. 11
- ↑ Niskanen, s. 14-15
- ↑ Niskanen, s. 12
- ↑ a b c d Niskanen, s. 16
- ↑ a b Leinster, s. 111
- ↑ Niskanen, s. 51-52
- ↑ Niskanen, s. 49
- ↑ a b Niskanen, s. 15
- ↑ Leinster, s. 93
- ↑ Leinster, s. 88
- ↑ a b Niskanen, s. 39
- ↑ Leinster, s. 90
- ↑ Leinster, s. 94
- ↑ Leinster, s. 104
- ↑ Leinster, s. 41-42
- ↑ Leinster, s. 53
- ↑ Niskanen, s. 76
- ↑ Leinster, s. 44
- ↑ a b Niskanen, s. 63
- ↑ Niskanen, s. 75
- ↑ Barr & Wells, Preface
- ↑ Haskell, nLab
- ↑ Barr & Wells, 2.2
- ↑ a b Fong & Spivak, Preface
- ↑ a b Bradley
- ↑ Coecke, Sadrzadeh & Clark
- ↑ Puuska, s. 41
- ↑ Heunen & Vicary
- ↑ Rosen
- ↑ Tuomi
- ↑ Ehresmann & Vanbremeersch














































































![{\displaystyle \left[{\mathcal {C}}^{op},\mathbf {Set} \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fba07162ef8aa3fb483ee7d2b39e2201c606ba8e)








![{\displaystyle Obj({\mathcal {C}})\rightarrow Obj\left(\left[{\mathcal {C}}^{op},\mathbf {Set} \right]\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/302df9c72468284a8e1de1239af3913d943c6c1f)
![{\displaystyle \mathbf {y} :{\mathcal {C}}\rightarrow \left[{\mathcal {C}}^{op},\mathbf {Set} \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f27719f585abc71dfc5d43ed4829a14d3a63383)





![{\displaystyle \left[{\mathcal {C}}^{op},\mathbf {Set} \right]\left(\mathbf {y} _{A},F\right)\simeq F(A)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/431cda736e0c45ce16de716f9d640711e3264eb9)


























