Kvanttitietokone

Kvanttitietokone on kehitteillä oleva tietokone, joka hyödyntää kvanttitilojen superpositiota ja sen tarjoamia erityisiä mahdollisuuksia. Mikäli suurempien kvanttitietokoneiden rakentaminen onnistuu, niillä voidaan ratkaista tiettyjä ongelmia huomattavasti klassisia tietokoneita nopeammin. Esimerkkejä ovat salausavainten tekijöihin jako ja erityisesti kvanttimekaniikan mallintaminen.[1]
Vuoteen 2019 mennessä kvanttitietokoneilla ei ollut ratkaistu mitään sellaista ongelmaa, jota ei voitaisi ratkaista klassisesti samassa ajassa, eli saavutettu niin sanottua kvanttiherruutta. Lokakuussa 2019 Google väitti 54-kubittisen Sycamore-kvanttitietokoneensa suorittaneen menestyksellisesti 200 sekunnissa tehtävän, jonka simuloimiseen klassiselta supertietokoneelta olisi Googlen oman arvion mukaan kulunut aikaa 10 000 vuotta.[2]. Kilpailija ja klassisten supertietokoneiden valmistaja IBM ei tuoreeltaan kiistänyt mahdollisesti saavutettua kvanttiherruutta mutta piti Googlen arviota koneensa suhteellisesta ylivoimasta räikeästi liioiteltuna.[3]
Taustaa
[muokkaa | muokkaa wikitekstiä]Jo vuonna 1959 amerikkalainen Nobel-palkittu fyysikko Richard Feynman huomasi, että elektronisten osien pienentyessä mikroskooppiseen mittaluokkaan kvanttimekaniikan ilmiöt tulevat yhä merkittävämmiksi. Hän vihjaisi, että niiden avulla voitaisiin kehittää yhä tehokkaampia tietokoneita. Erityisesti kvanttitietokonetutkijat toivovat pystyvänsä valjastamaan superpositioksi kutsutun ilmiön. Kvanttimekaniikan maailmassa objekteilla ei välttämättä ole selkeästi määrittynyttä tilaa. Asiaa havainnollistaa kuuluisa kaksoisrakokoe, jossa yksi valon fotoni kerrallaan läpäisee varjostimen, jossa on kaksi rakoa. Tällöin fotonit tuottavat interferenssikuvion superpositiona kaikista mahdollisista reiteistä. Jos taas yksi rako on suljettu tai mittalaitteella havainnoidaan, kumpaa reittiä pitkin fotoni kulki, interferenssikuvio katoaa. Seurauksena kvanttijärjestelmä ”on olemassa” kaikissa mahdollisissa tiloissa, kunnes mittaus ”romahduttaa” järjestelmän yhteen tilaan. Tämän ilmiön valjastaminen tietokoneessa mahdollistaa tietokoneiden laskentakykyjen suuren laajenemisen. Perinteinen binääritietokone käyttää binäärilukuja tai bittejä, jotka voivat olla kahdessa eri tilassa, jotka esitetään 0:na ja 1:nä. Näin ollen 4-bittinen tietokonerekisteri voi kerrallaan sisältää yhden 16:sta () mahdollisesta numerosta. Sitä vastoin kvanttibitti eli kubitti on samanaikaisesti aallon tapaisessa arvojen 0 ja 1 superpositiossa, jolloin 4-kubittinen tietokonerekisteri voi sisältää kaikki 16 lukua samanaikaisesti. Teoriassa kvanttitietokone voi siksi käyttää monia lukuja rinnakkaisesti, jolloin 30-kubittinen tietokone olisi verrattavissa digitaalisen tietokoneeseen, joka voi suorittaa 10 biljoonaa terafloppia sekunnissa (TFLOPS), mikä on verrattavissa nopeimpiin supertietokoneisiin.[4]
1980–1990-luvulla kvanttitietokoneiden teoria eteni merkittävästi Feynmanin alkuvaiheen spekuloinnista. Vuonna 1985 Oxfordin yliopiston David Deutsch kuvasi kvanttiporttien rakentamista universaalille kvanttitietokoneelle, ja vuonna 1994 AT&T:n työntekijä Peter Shor kehitti algoritmin (Shorin algoritmi) kvanttitietokoneelle jakamaan kokonaislukuja alkutekijöihinsä, mikä vaatisi niinkin vähän kuin 6 kubittia. Tosin lukujen jakaminen tekijöihin kohtuullisessa ajassa vaatisi paljon suuremman määrän kubitteja. Jos käytännöllinen kvanttitietokone rakennetaan, nykyiset kahden alkuluvun kertomiseen perustuvat kryptografian metodit tulevat hyödyttömiksi. Tämän kompensoimiseksi kvanttimekaaniset ilmiöt tarjoavat uusia, kvanttikryptografiaksi kutsuttuja keinoja viestinnän suojaamiseen. Oikean kvanttitietokoneen rakentaminen on kuitenkin osoittautunut vaikeaksi. Vaikka niiden potentiaali on valtava, niin ovat niiden vaatimuksetkin. Kvanttitietokoneen täytyy ylläpitää kubittien välistä koherenssia (tunnetaan kvanttilomittumisena) niin pitkään, että algoritmi saadaan suoritetuksi. Miltei vääjäämättömästi tapahtuvat vuorovaikutukset ympäristön kanssa (dekoherenssi) tuhoavat koherenssin. Virheiden havaitsemiseksi ja korjaamiseksi tarvitaankin siksi käytännön menetelmiä. Lisäksi on kehitettävä luotettavia menetelmiä tiedon lukemiseen, koska kvanttijärjestelmän havainnoiminen häiritsee sen tilaa.[4]
Toimintaperiaate
[muokkaa | muokkaa wikitekstiä]Tavallinen tietokone käyttää laskennassa bittejä. Jokainen bitti sisältää joko ykkösen tai nollan, ja laite suorittaa laskutoimitukset bittien arvoja muuttamalla. Kvanttitietokone käyttää laskutoimituksissa kubittejä. Yksi kubitti voi sisältää joko ykkösen, nollan tai, tyypillisesti, ykkösen ja nollan superposition, jolloin kummankin toteutumiselle on oma todennäköisyytensä. Tilannetta havainnollistetaan tavallisesti Schrödingerin kissana tunnetulla ajatuskokeella[5].
Mahdollisten tilojen suuren määrän ansiosta kvanttitietokone voi suorittaa suuren määrän laskutoimituksia paljon nopeammin kuin binääritietokoneet. Kvanttilaskennassa tutkijat tavallisesti eristävät molekyylin, atomin tai subatomisen hiukkasen, manipuloivat sen spiniä ja mittaavat tulokset. Tähän tarkoitukseen on eristetty myös valon fotoneita. Toistaiseksi manipulointi on onnistunut vain kokeellisella tasolla. Kvanttilaskennan uranuurtajina olivat Paul Benioff (1980)[6], Juri Manin (1980)[7], Richard Feynman (1982)[8] ja David Deutsch (1985)[9] . Onnistuneet kokeet kvanttitietokoneiden saralla alkoivat 1990-luvun jälkipuoliskolla. Kyky suorittaa suuria määriä laskutoimituksia ja tehokkuus rinnakkaisprosessoinnissa tarkoittavat, että kvanttitietokoneita luultavasti käytetään tietoturvaa ja kryptografiaa vaativissa tehtävissä. Toinen mahdollinen hyöty kvanttitietokoneista tulee olemaan koon pieneneminen. Kuitenkin tähän mennessä koneisto, jota käytetään näissä projekteissa, on vieläkin melko suurta.[10]
Superposition ansiosta kvanttitietokoneilla on potentiaalia ratkaista joitakin ongelmia klassisia tietokoneita nopeammin. Kvanttitietokoneessa moni luku on superpositiotilassa, ja kvanttitietokone suorittaa tätä kautta laskutoimituksen kaikille näille luvuille rinnakkain. Kvanttitietokoneessa yhden kubitin tila kaukovaikuttaa toisen tilaan ilman aikaviivettä, vaikka ne olisivat hyvinkin kaukana toisistaan. Tämä ominaisuus mahdollistaa tiettyjen, aiemmin liian suuren laskentatehon vaatineiden ongelmien tehokkaan ratkaisemisen. Kuuluisa esimerkki tästä on kvanttitietokoneelle suunniteltu Shorin algoritmi (1994), jolla luku voidaan jakaa tekijöihinsä tehokkaasti. Algoritmia voitaisiin käyttää murtamaan nykyisin yleisesti käytetty RSA-salakirjoitus.lähde?
Kvanttitietokoneiden rajoituksena on se, että mittaushetkellä superpositiot romahtavat. Siksi kvanttitietokoneella kyetään ratkaisemaan vain sellaisia ongelmia, joiden vastaus löytyy yhdellä kysymyksellä. Useampia kysymyksiä ongelman ratkaisemiseksi ei siis voida kysyä.lähde?
Kubitit
[muokkaa | muokkaa wikitekstiä]- Pääartikkeli: Kubitti
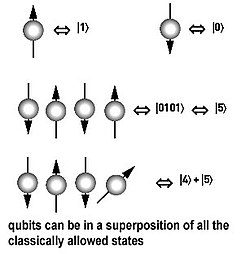
Tietoa varastoivia yksikköjä kutsutaan kubiteiksi (”kvanttibitti”). Fyysisesti ne voivat olla hiukkasia tai suprajohtavia virtasilmukoita, loogisina kubitteina myös niiden ryhmiä. Toisin kuin klassisessa tietokoneessa, jossa kussakin transistorissa on käytettävissä rajaton määrä varauksenkuljettajia, kvanttitietokoneessa yhdenkin kubitin häiriö tai menetys riittää laskun piloille menemiseen. Kvanttikoherenssi on vaikea säilyttää ja vaatii kubitin suojaamista hyvin ympäristön vaikutukselta. Energianmenetys |1> -> |0> tapahtuu kubitille vakiotodennäköisyydellä aikayksikössä. Toinen häiriö ovat satunnaiset muutokset kubitin energiassa, jotka muuttavat sen suhteellista tilaa. Usein myös tämän häiriön todennäköisyys kasvaa ajan myötä.[11] Kubitit pysyvät tilassaan niin lyhyen aikaa, että tarvitaan keinoja, joilla joko voidaan jatkaa niiden pysymistä superpositiossa tai tehdä järjestelmä muuten sietämään virheitä paremmin. Toivottavaa olisi, että koko lasku voitaisiin suorittaa mahdollisimman nopeasti ja vähillä operaatioilla, koska jokainen operaatio osaltaan horjuttaa kubitin tilaa.[12]
Fyysisinä kubitteina on kokeiltu erilaisia objekteja: elektroneja, ioneja (atomeja) ja suprajohtavassa tilassa olevia virtasilmukoita. Toimiakseen kubittina valitulla kohteella tulee olla erityinen kvanttifysikaalinen ominaisuus, jota hyödyntää. Elektronin tapauksessa se on yleensä spin, ioneilla jokin sen elektronitiloista, joka voidaan valita vakaaksi, kuten atomikelloissa.[13]
Suprajohtavuutta ja Josephsonin liitosta hyödyntämällä voidaan normaaliin virtapiiriin luoda oskillaattori, joka toimii kubittina. Tätä menetelmää on hyödyntänyt muun muassa yritys D-Wave Systems.[14]
Virheenhallinta
[muokkaa | muokkaa wikitekstiä]Kubitit ovat alttiita ulkoisille häiriöille ja niiden sietokykyä järjestelmässä voidaan kasvattaa muodostamalla loogiset kubitit useista yksittäistä, fyysisistä kubiteistä. Tällöin yksittäisen fyysisen kubitin tilan pilaava häiriö ei riitä estämään laskun etenemistä ja kubittien tilojen seuranta voidaan suorittaa yksi fyysinen osa kerrallaan. Näin vähennetään ryhmän yksittäiseen jäseneen kohdistuvaa rasitusta ja kasvatetaan sen ”eliniänodotetta”.[15]
Ohjelmointi ja algoritmit
[muokkaa | muokkaa wikitekstiä]- Pääartikkeli: Kvanttiohjelmointi
Laskenta perustuu amplitudien interferenssiin. Tavoitteena on saada matemaattinen ongelma sellaiseen muotoon, että kvanttitietokoneessa oikea vastaus vahvistaa itseään, kun taas väärät vastaukset päinvastoin pyrkivät heikentämään itseään. Jos ongelmaa ei voida saattaa tällaiseen muotoon, kvanttitietokoneella ei luultavasti voida saada nopeusetua.[1]
Toteutustapoja
[muokkaa | muokkaa wikitekstiä]Suunnitelmia kvanttitietokoneiden rakentamiseen on ehdotettu. Vaikka moni niistä havainnollistaa perusperiaatteet, mikään ei ole edistynyt kokeellista käyttöä pitemmälle[4]. Kolme lupaavinta lähestymistapaa ovat suprajohteet[16], ioniloukut[4] ja kvanttipisteet[4].
Vuonna 1998 Isaac Chuang Los Alamos National Laboratorysta, Neil Gershenfeld Massachusetts Institute of Technologystä (MIT) ja Mark Kubinec Kalifornian yliopistosta Berkeleyssä kehittivät ensimmäisen, 2-kubittisen kvanttitietokoneen, johon voisi syöttää dataa ja saada tulokseksi ratkaisun. Vaikka heidän järjestelmänsä oli koherentti vain muutaman nanosekunnin ja triviaali merkittävien ongelmien ratkaisemisen kannalta, se havainnollisti kvanttitietokoneiden toimintaperiaatteita. Subatomisen hiukkasen eristämisen sijaan he hajottivat suuren määrän kloroformimolekyylejä (CHCL3) huoneenlämpöiseen veteen ja käyttivät magneettikenttää sen hiili- ja vetyatomien spinien orientoimiseen.[17] Koska normaalilla hiilellä ei ole magneettista spiniä, heidän ratkaisunsa oli käyttää hiilen isotooppia 13. Ulkoisen magneettikentän suuntainen spin voitiin tällöin tulkita tulkita 1:ksi ja vastasuuntaisena 0:ksi, ja vety- ja hiili-13-ytimiä voitiin kollektiivisesti pitää 2-kubittisena järjestelmänä. Ulkoisen magneettikentän lisäksi radiotaajuista pulssia käytettiin spin-tilojen kääntämiseen yhdensuuntaisen ja vastasuuntaisen tilan välillä. Lisäpulsseja lähetettiin yksinkertaisen algoritmin suorittamiseen ja järjestelmän lopputilan tutkimiseen. Tämän tapaista kvanttitietokonetta voi laajentaa käyttämällä molekyylejä, joissa on enemmän yksilöllisesti kohdistettavia atomiytimiä. Vielä maaliskuussa 2000 Emanuel Knill, Raymond Laflamme ja Rudy Martinez Los Alamokselta ja Ching-Hua Tseng MIT:stä kertoivat valmistaneensa 7-kubittisen tietokoneen käyttämällä trans-krotonaldehydihappoa. Monet tutkijat suhtautuvat kuitenkin epäillen tämän magneettisen menetelmän laajentamiseen yli 10:n ja 15 kubitin, koska koherenssi pienenee nopeasti atomiytimissä.[4]
Viikko ennen 7 kubitin tietokoneen julkaisemista fyysikko David Wineland ja hänen kollegansa (NIST):stä kertoivat tehneensä 4 kubitin kvanttitietokoneen lomittamalla neljä ionisoitunutta berylliumatomia sähkömagneettiseen ”loukkuun”. Sen jälkeen, kun ionit oli vangittu lineaarisella järjestelyllä, lasersäde jäähdytti hiukkaset lähelle absoluuttista nollapistettä ja synkronoi niiden spin-tilat. Lopuksi hiukkaset lomitettiin laserilla, mikä loi superposition "spin ylös"- ja "spin alas" -tilojen välille samanaikaisesti kaikille neljälle ionille. Jälleen tämä havainnollisti kvanttitietokoneiden perusperiaatteet, mutta tämänkin tekniikan laajentaminen käytännöllisiin mittasuhteisiin on ongelmallista.[4]
Puolijohteisiin perustuvat kvanttitietokoneet ovat yksi toteutusvaihtoehto. Eräs lähestymistapa on joukko eristettyjä vapaita elektroneja (kubitteja), jotka sijaitsevat erittäin pienillä alueilla, joita kutsutaan kvanttipisteiksi. Kukin kahdesta spin-tilasta tulkitaan nollaksi tai ykköseksi. Vaikka tämä on altis dekoherenssille, sellaiset kvanttitietokoneet pohjautuisivat hyvin tunnetuille kiinteän aineen tekniikoille ja niihin voitaisiin soveltaa integroitujen piirien mittakaavan teknologiaa. Lisäksi suuri joukko identtisiä kvanttipisteitä voitaisiin mahdollisesti tehdä yhdelle sirulle. Siru toimii ulkoisessa magneettikentässä, joka ohjaa elektronien spin-tiloja, kun taas naapurielektronit ovat heikosti kytkeytyneet toisiinsa (lomittuneet) kvanttimekaanisten ilmiöiden seurauksena. Kokoelma päällekkäisiä lankaelektrodeja sallii yksittäisten kvanttipisteiden käsittelyn, algoritmien suorittamisen ja lopputuloksen päättelemisen. Sellaista järjestelmää täytyy käyttää lämpötiloissa lähellä absoluuttista nollapistettä, jotta ympäristön dekoherenssi saataisiin minimoitua, mutta siinä voidaan toteuttaa järjestelmiä, joissa on suuri määrä kubitteja.[4]
Tulevaisuudessa kvanttitietokoneita saatetaan käyttää koodinmurtamisessa (katso kryptografia) ja suurien tietokantojen[17] hakemisessa. Teoreetikot kemiassa, tietojenkäsittelytieteessä, matematiikassa ja fysiikassa työstävät kvanttitietokoneiden rajoituksia ja mahdollisuuksia[17].
Kehitys
[muokkaa | muokkaa wikitekstiä]
Hiljattain on rakennettu pieniä kvanttitietokoneita, ja tutkimus jatkuu. Kanadalainen D-Wave Systems yritti valmistaa kaupallisia laskentapalveluja tarjoavan, tunneloitumistekniikkaan perustuvan kvanttitietokoneen vuoteen 2008 mennessä. Yritys havainnollisti omien sanojensa mukaan 16-kubittistä kvanttitietokonetta vuonna 2007, mutta tuloksia on kritisoitu.[18]
Vuonna 2013 D-Waven 512 kubitin kvanttitietokoneen ostivat muun muassa Lockheed Martin ja Google.[19]
IBM on kehittänyt kvanttitietokoneen, joka on yleiskäyttöinen toisin kuin D-Wave:n kvanttitietokone, mutta IBM:n toteutus on viiden kubitin kapasiteetilla.[20]
Vuonna 2017 D-Wave julkisti 2 000 kubitin D-Wave 2000Q -mallin.[21][22] Tätä mallia on kritisoitu sen kubittien rakenteen ja toiminnan eroavaisuuksista verrattuna perinteisiin kvanttikoneisiin. Kriitikoiden mukaan D-Wave 2000Q:n kubitit eivät ole yhtä kestäviä eivätkä tarjoa yhtä tarkkaa fyysistä käsittelykykyä (manipulointikykyä) kuin perinteisissä kvanttikoneissa. Lisäksi D-Waven kvanttitietokoneet pystyvät ratkaisemaan vain yhden tyyppisiä tehtäviä, nimittäin optimointiongelmia.[23]
Google ilmoitti vuonna 2017 aikeistaan julkaista oman ratkaisunsa, mutta tarkkaa julkaisuajankohtaa ei ilmoitettu.[24] IBM:n ratkaisussa epätarkkuudet laskennassa on saatu rajattua kahden ja neljän prosentin virhemarginaaliin beryllium-yhdisteen mallinnuksessa.[25]
Vuonna 2019 Googlen tutkijat ilmoittivat suorittaneensa 53-qubittisen Sycamore-kvanttitietokoneen avulla 200 sekunnissa tehtävän, jonka laskeminen klassisella periaatteella toimivalla supertietokoneella olisi kestänyt 10 000 vuotta, ja siten saavuttaneensa kvanttiherruuden[26][2]. IBM:n tutkijat kiistivät tämän väittäen, että klassinen tietokone voisikin ratkaista saman ongelman jo 2,5 päivässä ja vieläpä suuremmalla tarkkuudella[3][2]. Siten kyseessä olisi ainoastaan etu, ei "herruus"[2]. Googlen tutkijat saivat kuitenkin tukea Texasin yliopiston tietojenkäsittelyn professorilta Scott Aaronsonilta sekä Aalto-yliopiston ja VTT:n kvanttiteknologian professorilta Mikko Möttöseltä, jonka mukaan IBM:n väite ei riitä tuhoamaan Googlen saavutusta, ja Google julisti edelleen pitävänsä kvanttiherruutta hallussaan[27].

Syyskuussa 2019 julkisuuteen vuoti artikkeli, jonka Google ensin veti pois mutta julkaisi myöhemmin uudelleen. Artikkelissa kvanttitietokonetta käytettiin ratkaisemaan korkean virhetason ongelma, joka perinteisillä tietokoneilla olisi vaatinut huomattavan paljon aikaa.[28][29][30] Googlen mukaan ongelma valittiin ratkaisukohteeksi nimenomaan kvanttitietokoneiden kyvyllä tuottaa tuloksia korkeasta virhemäärästä huolimatta.[29] Tavoitteena oli osoittaa kvanttietokoneiden pystyvän olemaan ylivertaisia.[28]
Kiinalainen Origin Quantum kertoi toimittaneensa asiakkaalle 28-qubitin Wuyuan-kvanttitietokoneen vuonna 2021. Kiina on siis kolmas valtio, jossa pystytään rakentamaan käyttökelpoinen kvanttitietokone. Yhtiön perustivat Kiinan tiede- ja teknologiayliopiston kvanttitutkijat Guo Guoping ja Guo Guangcan vuonna 2017.[31][32]
Vuonna 2023 IBM ilmoitti 1 121 kubitin Condor-prosessorin julkaisemisesta ja suunnitelmiensa päivittämisestä. Päivityksen mukaan IBM ennakoi toimivaa virheenkorjausta vuosikymmenen loppuun mennessä. Joitakin yksinkertaisia kvanttialgoritmeja voi suorittaa nykyisellä laitteistolla.[33]
Suomessa
[muokkaa | muokkaa wikitekstiä]Vuonna 2021 Teknologian tutkimuskeskus VTT ja suomalainen startup IQM saivat valmiiksi Suomen ensimmäisen kvanttitietokoneen[34]. Koneessa on viisi kubittia[34]. Sen nimi on Helmi[35]. Kone sijaitsee Espoon Micronovassa[35]. Toinen, 20 kubitin kone valmistui vuonna 2023[36]. VTT:n ja IQM:n tavoitteena on rakentaa 50 kubitin kvanttitietokone vuoteen 2024 mennessä[34].
Vuonna 2021 Suomessa toimi 15 kvanttitietokonealan yritystä, joiden yhteenlaskettu liikevaihto lähestyi sataa miljoonaa euroa. Näihin kuuluu esimerkiksi kryostaatteja valmistava Bluefors. [34]
Lähteet
[muokkaa | muokkaa wikitekstiä]- Sank, Daniel T.: Fast, Accurate State Measurement in Superconducting Qubits 2015. University of California. Viitattu 5.6.2016.
Viitteet
[muokkaa | muokkaa wikitekstiä]- ↑ a b John Horgan: Scott Aaronson Answers Every Ridiculously Big Question I Throw at Him 21.4.2016. Scientific American. Viitattu 5.6.2016. (englanniksi)
- ↑ a b c d Elizabeth Gibney: Hello quantum world! Google publishes landmark quantum supremacy claim. Nature, 23.10.2019, nro 574, s. 461–462. doi:10.1038/d41586-019-03213-z. Artikkelin verkkoversio. (englanniksi)
- ↑ a b On “Quantum Supremacy” IBM Research Blog. 22.10.2019. Viitattu 23.10.2019. (englanniksi)
- ↑ a b c d e f g h Holton, William Coffeen: quantum computer. Encyclopædia Britannica. Encyclopædia Britannica Ultimate Reference Suite, 2015. ISBN 978-1625132963. (englanniksi)
- ↑ Brown, Julian: ”Tulkintakysymys”, ”3 Kvanttisalaliiton logiikka”, Kvanttitietokone. Sitaatti, s. 109–110: ”Kissa pannaan laatikkoon, jonka Schrödinger kuvasi ”pirulliseksi laitteeksi”. Siinä on pieni kappale radioaktiivista ainetta, jonka puoliintumisaika on valittu siten, että minuutin mittaan on 50 prosentin mahdollisuus, että yksi atomi hajoaa.”. Suomentanut Kimmo Pietiläinen. Helsinki: Terra cognita, 2001. ISBN 952-5202-42-9.
- ↑ Benioff, Paul: The computer as a physical system: A microscopic quantum mechanical Hamiltonian model of computers as represented by Turing machines. Journal of Statistical Physics, 1980, 22. vsk, nro 5, s. 563–591. Journal of Statistical Physics. doi:10.1007/BF01011339. Bibcode:1980JSP....22..563B. (englanniksi)
- ↑ Manin, Juri I.: Вычислимое и невычислимое (Vytšislimoje i nevytšislimoje) (Laskettavissa ja ei-laskettavissa). Sov.Radio, 1980, s. 13–15. Sov.Radio. Artikkeli (Zip). Viitattu 8.11.2015. (venäjäksi)
- ↑ Feynman, Richard: Simulating Physics with Computers. International Journal of Theoretical Physics, .Kesäkuu 1981, 21. vsk, nro 6, s. 467–488. International Journal of Theoretical Physics. PubMed:24948715. doi:10.1007/BF02650179. Bibcode:1982IJTP...21..467F. Artikkeli. Viitattu 21.20.2015. (englanniksi)
- ↑ Deutsch, David: Quantum theory, the Church-Turing principle and the universal quantum computer. Proceedings of the royal society of London, series A: mathematical and physical sciences, 1985, 400. vsk, nro 1818, s. 97–117. Lontoo: Royal society of London. doi:https://doi.org/10.1098/rspa.1985.0070. ISSN 0080-4630. (englanniksi)
- ↑ quantum computing. Versio 16.00 Windows XP, 2000, 9x, Me, and NT. 2003 Grolier Multimedia Encyclopedia, Grolier Interactive Inc, 2002. ISBN 043965419. (englanniksi)
- ↑ Sank 11–14
- ↑ Sank 16
- ↑ Sank 16–19
- ↑ Sank 20–25
- ↑ Sank 29–32
- ↑ Stancil, Daniel D. & Byrd, Gregory T.: Principles of Superconducting Quantum Computers. John Wiley & Sons, 2022. ISBN 978-1-119-75072-7 (kovakantinen) ja ISBN 978-1-119-75074-1 (E-kirja). Finna.fi-tietokanta. (englanniksi)
- ↑ a b c Snyder, Timothy Law: ”Artikkeli: Computer: XIV. The future of computers”, Computer. Sitaatti: "Future uses of quantum computers could include code breaking (see cryptography) and large database queries. Theorists of chemistry, computer science, mathematics, and physics are now working to determine the possibilities and limitations of quantum computing.". Encarta Multimedia Encyclopedia, Microsoft® Student 2009 [DVD], 2009. (englanniksi)
- ↑ Aaronson, Scott: The Orion Quantum Computer Anti-Hype FAQ (Scott Aarsonin blogi, jossa kritisoidaan mm. D-Waven kvanttitietokoneita.) Scottaaronson.com. Viitattu 22.7.2016. (englanniksi)
- ↑ Hardy, Quentin: Google Buys a Quantum Computer The New York Times. 2013. Viitattu 3.6.2013. (englanniksi)
- ↑ How IBM’s new five-qubit universal quantum computer works Ars Technica. Viitattu 29.1.2017. (englanniksi)
- ↑ Explaining the upside and downside of D-Wave’s new quantum computer Ars Technica. Viitattu 29.1.2017. (englanniksi)
- ↑ D-Wave Announces D-Wave 2000Q Quantum Computer and First System Order D-Wave Systems. Arkistoitu 27.1.2017. Viitattu 29.1.2017. (englanniksi)
- ↑ Dom Galeon: The Most Controversial Quantum Computer Ever Made Just Got an Upgrade Futurism. 2017. futurism.com. Viitattu 9.2.2017. (englanniksi)
- ↑ Google’s New Chip Is a Stepping Stone to Quantum Computing Supremacy technology review. Viitattu 23.4.2017. (englanniksi)
- ↑ Kahn, Jeremy: IBM Makes Breakthrough in Race to Commercialize Quantum Computers Bloomberg. Viitattu 17.9.2017. (englanniksi)
- ↑ Frank Arute, Kunal Arya, Ryan Babbush, Dave Bacon, Joseph C. Bardin, Rami Barends: Quantum supremacy using a programmable superconducting processor. Nature, 2019-10, nro 7779, s. 505–510. doi:10.1038/s41586-019-1666-5. ISSN 1476-4687. Artikkelin verkkoversio. (englanniksi)
- ↑ IBM kiistää Googlen kvanttiherruuden, mutta turhaan, sanovat asiantuntijat Helsingin Sanomat. 26.10.2019. Viitattu 26.10.2019.
- ↑ a b Dennis Overbye: Quantum Computing Is Coming, Bit by Qubit 23.10.2019. New York Times. Viitattu 29.10.2019. (englanniksi)
- ↑ a b John Timmer: Here’s what the people who claimed Google’s quantum supremacy have to say about it Ars Technica. 24.10.2019. Viitattu 29.10.2019. (englanniksi)
- ↑ John Timmer: Paper leaks showing a quantum computer doing something a supercomputer can’t Ars Technica. 24.9.2019. Viitattu 29.10.2019. (englanniksi)
- ↑ Chinese Scientists make Quantum Leap scmp.com News
- ↑ Quantum Computer 495290 slicon.co
- ↑ John Timmer: IBM releases 1,000+ qubit processor, roadmap to error correction arstechnica.com. 4.12.2023. Viitattu 5.12.2023. (englanniksi)
- ↑ a b c d Näin toimii juuri valmistunut kvanttitietokone – Suomi teki ensimmäisten joukossa koneen, jonka monituhatkertainen laskentanopeus mullistaa lukuisat alat Yle Uutiset. 30.11.2021. Viitattu 1.11.2022.
- ↑ a b Mikko Pulliainen: Näin VTT:n kvanttitietokone surisee ja piipittää – kuluttaa kuin sähkökiuas Mikrobitti. Viitattu 10.12.2022.
- ↑ Suomen toinen kvanttitietokone on nyt valmis: tätä se tarkoittaa Yle Uutiset. 10.10.2023. Viitattu 10.10.2023.
Kirjallisuutta
[muokkaa | muokkaa wikitekstiä]Yleistajuista kirjallisuutta
[muokkaa | muokkaa wikitekstiä]Suomeksi
[muokkaa | muokkaa wikitekstiä]- Brown, Julian: Kvanttitietokone. (Minds, Machines, and the Multiverse: The Quest for the Quantum Computer, 2000.) Suomentanut Kimmo Pietiläinen. Helsinki: Terra cognita, 2001. ISBN 952-5202-42-9. Finna.fi-tietokanta.
- Turton, Richard: Kvanttipiste. (The Quantum Dot: A Journey into the Future of Microelectronics.) Suomentanut Kimmo Pietiläinen. Art House, 1996. ISBN 951-884-208-6. Finna.fi-tietokanta.
- Hänninen, Veijo: Tavoitteena kvanttitietokone. Omakustanne, 2018. ISBN 978-951-568-005-1. Finna.fi-tietokanta.
- Kajamaa, Jaakko: Atomitason tekniikka. 1. painos. Porvoo; Helsinki: WSOY, 1991. ISBN 951-0-17221-9. Finna.fi-tietokanta.
- Baeyer, Hans Christian von: Kesytetty atomi: kun mikromaailma muuttuu näkyväksi. 1. painos. Suomentanut Kimmo Pietiläinen. Helsinki: Art House, 1993. ISBN 951-884-118-7. Finna.fi-tietokanta.
Englanniksi
[muokkaa | muokkaa wikitekstiä]- Seigfried, Tom: The Bit and the Pendulum: From Quantum Computing to M Theory. New York: Wiley, 2000. ISBN 0-471-32174-5. Finna.fi-tietokanta. (englanniksi)
- Rudolph, Terry: Q is for quantum. —, 2017. ISBN 978-0-9990635-0-7. Finna.fi-tietokanta. (englanniksi)
- Coecke, Bob & Gogioso Stefano: Quantum in Pictures: A New Way to Understand the Quantum World. Quantinuum, 2023. ISBN 978-1-7392147-1-5. Finna.fi-tietokanta. (englanniksi)
- Wong, Thomas G.: Introduction to Classical and Quantum Computing. Huomautus: tekijä itse on julkaissut kirjan kotisivuillaan. Arkistoitu 22.12.2023. Rooted Grove, 2022. ISBN 979-8-9855931-0-5 (nidottu) & ISBN 979-8-9855931-1-2 (sidottu). Teoksen verkkoversio (PDF). (englanniksi)
- Hurley, William W. & Smith, Bud E.: Quantum Computing for Dummies. Osa keltanokille -kirjasarjaa. Hoboken, New Jersey: John Wiley & Sons, 2023. ISBN 978-1-119-93390-8 (nidottu) ja ISBN 1-119-93391-9 (E-kirja). Finna.fi-tietokanta. (englanniksi)
- Bernhardt, Chris: Quantum computing for everyone. Cambridge, Massachusetts: The MIT Press, 2020. ISBN 978-0-262-53953-1 (nidottu) & ISBN 978-0-262-35091-4 (E-kirja). Finna.fi-tietokanta. (englanniksi)
Yliopistotason oppikirjoja (englanniksi)
[muokkaa | muokkaa wikitekstiä]- Nielsen, Michael A. & Chuang, Isaac L.: Quantum computation and quantum information. 2. painos. Cambridge University Press, 2010. ISBN 978-1-107-00217-3 (sidottu) & ISBN 978-1-107-61919-7 (nidottu). Finna.fi-tietokanta. doi:10.1017/CBO9780511976667. (englanniksi)
- Jaeger, Gregg: Quantum Information: An Overview. Springer, 2007. ISBN 978-0-387-35725-6 (sidottu), ISBN 978-1-4419-2258-8 (nidottu) ja ISBN 978-0-387-36944-0 (E-kirja). Finna.fi-tietokanta. doi:10.1007/978-0-387-36944-0. (englanniksi)
- Nakahara, Mikio & Ohmi, Tetsuo: Quantum Computing: From Linear Algebra to Physical Realizations. Boca Raton: CRC Press, 2008. ISBN 978-0-7503-0983-7 (sidottu) ja ISBN 978-1-4200-1229-3 (E-kirja). Finna.fi-tietokanta. (englanniksi)
- Schumacher, Benjamin & Westmoreland, Michael D.: Quantum Processes Systems, and Information. Cambridge University Pres, 2010. ISBN 978-0-521-87534-9. Finna.fi-tietokanta. (englanniksi)
- Kasirajan, Venkateswaran: Fundamentals of Quantum Computing: Theory and Practice. Springer, 2021. ISBN 978-3-030-63691-3. Finna.fi-tietokanta. doi:10.1007/978-3-030-63689-0. (englanniksi)
- Hidary, Jack D.: Quantum Computing: An Applied Approach. 2. painos. Springer, 2021. ISBN 978-3-030-83273-5. Finna.fi-tietokanta. doi:10.1007/978-3-030-83274-2. (englanniksi)
- Djordjevic, Ivan B.: Quantum Information Processing, Quantum Computing, and Quantum Error Correction: An Engineering Approach. 2. painos. Academic Press, 2021. ISBN 978-0-12-821982-9. doi:10.1016/C2019-0-04873-X. (englanniksi)
- Bolívar, Nelson (toim.): Handbook of Quantum Computation. Arcler Press, 2018. ISBN 978-1-77361-101-3. Finna.fi-tietokanta. (englanniksi)
- Mermin, N. David: Quantum Computer Science: An Introduction. Cambridge University Press, 2007. ISBN 978-0-521-87658-2. Finna.fi-tietokanta. (englanniksi)
- Yanofsky, Noson S. & Mannucci, Mirco A.: Quantum Computing for Computer Scientists. Cambridge University Press, 2008. ISBN 978-0-521-87996-5. Finna.fi-tietokanta. (englanniksi)
- Hirvensalo, Mika: Quantum computing. 2. painos, osa kirjasarjaa: Natural Computing Series (NCS). Springer, 2010. ISSN 1619-7127 & E-ISSN 2627-6461. ISBN 978-3-6420-7383-0 (nidottu), ISBN 978-3-662-09636-9 (E-kirja). Finna.fi-tietokanta. doi:10.1007/978-3-662-09636-9. (englanniksi)
- Gruska, Jozef: Quantum computing. McGraw-Hill, 1999. ISBN 0-07-709503-0. Finna.fi-tietokanta. (englanniksi)
- Benenti, Giuliano; Casati, Giulio; Rossini, Davide; Strini, Giuliano: Principles of Quantum Computation and Information: A Comprehensive Textbook. 2. painos. World Scientific, 2019. ISBN 978-981-3237-22-3. (englanniksi)
- Kurgalinm, Sergei & Borzunov, Sergei: Concise Guide to Quantum Computing: Algorithms, Exercises, and Implementations. Springer Cham, 2021. ISSN: 1868-0941 & E-ISSN: 1868-095X. ISBN 978-3-030-65054-4. Finna.fi-tietokanta. doi:10.1007/978-3-030-65052-0. (englanniksi)
- Manenti, Riccardo & Motta, Mario: Quantum Information Science. Oxford University Press, 2023. ISBN 978-0-19-878748-8 (sidottu) ja ISBN 978-0-19-109140-7 (E-kirja). Libris-tietokanta. (englanniksi)
- Müller, Rainer & Greinert, Franziska: Quantum Technologies: For Engineers. Berlin: De Gruyter, 2023. ISBN 978-3-11-071744-0 (nidottu), ISBN 978-3-11-071745-7 (E-kirja, PDF) ja ISBN 978-3-11-071750-1 (E-kirja, EPUB). Finna.fi-tietokanta. doi:10.1515/9783110717457. (englanniksi)
Kvanttilaskennan matematiikkaa (englanniksi)
[muokkaa | muokkaa wikitekstiä]- Woody, Leonard S.: Essential Mathematics for Quantum Computing: A Beginner’s Guide to Just the Math You Need Without Needless Complexities. Packt Publishing, 2022. ISBN 978-1-80107-314-1. Finna.fi-tietokanta. (englanniksi)
- Bez, Helmut & Croft, Tony: Quantum computation. CRC Press, 2023. ISBN 978-1-032-20648-6. Finna.fi-tietokanta. (englanniksi)
- Scherer, Wolfgang: Mathematics of Quantum Computing: An Introduction. Alkuperäisteos: Mathematik der Quanteninformatik: Eine Einführung. Springer, 2019. ISBN 978-3-030-12357-4. Finna.fi-tietokanta. (englanniksi)
- Yan, Song Y.: Quantum Computational Number Theory. Ensijulkaistu E-kirjana vuonna 2015 ja myöhemmin 2016 kovakantisena ja 2018 pehmeäkantisena. Springer, 2015. ISBN 978-3-319-25821-8 (sidottu), ISBN 978-3-319-79846-2 (nidottu) ja ISBN 978-3-319-25823-2 (E-kirja). Finna.fi-tietokanta. doi:10.1007/978-3-319-25823-2. (englanniksi)
- Pelayo, Fernando L. & Mezzini, Mauro (toim.): Quantum Computing Algorithms and Computational Complexity. Mathematics (lehti), erityisnumero, osio: Mathematics and Computer Science, Verkkoversio HTML, Finna.fi-tietokanta. Basel, Sveitsi: Multidisciplinary Digital Publishing Institute (MDPI), 2022. ISSN 2227-7390. ISBN 978-3-0365-7746-3 (sidottu) ISBN 978-3-0365-7747-0 (E-kirja). Teoksen verkkoversio (PDF). doi:10.3390/books978-3-0365-7747-0. (englanniksi)
- Lipton, Richard J. & Regan, Kenneth W.: Introduction to Quantum Algorithms via Linear Algebra. 2. painos. MIT Press, 2021. ISBN 978-0-262-04525-4. Finna.fi-tietokanta. (englanniksi)
- Sutor, Robert S.: Dancing with Qubits: Find out how quantum computing works and how you can use it to change the world. 2. painos. Packt Publishing, 2024. ISBN 978-1-83763-675-4. Finna.fi-tietokanta. (englanniksi)
- Barry, Burd: Quantum Computing Algorithms: Discover how a little math goes a long way. Birmingham: Packt Publishing, 2023. ISBN 978-1-80461-737-3 (nidottu), ISBN 978-1-80461-056-5 (E-kirja). Finna.fi-tietokanta. (englanniksi)
- Brylinski, Ranee K. & Chen, Goong (toim.): Mathematics of Quantum Computation. CRC Press, 2002. ISBN 978-0-367-39635-0. Finna.fi-tietokanta. (englanniksi)
- Pittenger, Arthur O.: An Introduction to Quantum Computing Algorithms. Boston: Birkhäuser, 2000. ISBN 978-0-8176-4127-6 (kovakantinen), ISBN 978-1-4612-7127-7 (pehmeäkantinen) ja ISBN 978-1-4612-1390-1 (E-kirja). Finna.fi-tietokanta. (englanniksi)
Tutkimusta & raportteja
[muokkaa | muokkaa wikitekstiä]- Raatikainen, Anu: Kvanttioperaatioiden matematiikka ja Shorin algoritmi. Pro gradu -tutkielma, 2006. Turun yliopisto: matematiikka. Finna.fi-tietokanta.
- La Cour, Brian R. & Benenti, Giuliano (toim.): Advances in Quantum Computing. Entropy (lehti), erityisnumero, osio: Quantum Information, Verkkoversio HTML. Basel, Sveitsi: Multidisciplinary Digital Publishing Institute (MDPI), 2024. ISSN 1099-4300. ISBN 978-3-7258-0020-9 (sidottu) ISBN 978-3-7258-0019-3 (E-kirja). Teoksen verkkoversio (PDF). doi:10.3390/books978-3-7258-0019-3. (englanniksi)
Aiheesta muualla
[muokkaa | muokkaa wikitekstiä]- Trudeau versus the experts: Quantum computing in 35 seconds Macleans.ca 19.4.2016
- Aaronson, Scott: Shor – I'll do it (Scott Aaronsonin blogi) scottaaronson.com. 24.2.2007. Viitattu 5.6.2016.
| Yleiset | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Kvanttiviestintä | |||||||||
| Kvanttialgoritmit | |||||||||
| Kvanttilaskennan monimutkaisuusteoria | |||||||||
| Kvanttilaskennan mallit | |||||||||
| Kvanttisuorittimien suorituskykyindikaattorit | |||||||||
| Dekoherenssin ennaltaehkäisy | |||||||||
| Fyysiset toteutustavat |
|
| ||||||||||||||
