Elliptinen käyrä
Matematiikassa elliptinen käyrä on epäsingulaarinen tasokäyrä, jonka määrittelee yhtälö
- ,
jossa a ja b kuuluvat annettuun kuntaan K. Käyrän epäsingulaarisuus tarkoittaa, että käyrässä ei ole teräviä kohtia ja se ei leikkaa itseään. Elliptiset käyrät vastaavat toruksen upottamista kompleksiseen projektiiviseen avaruuteen. Tällainen upotus voidaan tehdä jokaisessa kunnassa, joten sanotaan, että elliptiset käyrät ovat kunnan K, johon on lisätty yksi piste, epäsingulaarisia projektiivisten varistojen algebrallisia käyriä, joiden genus on 1.
Elliptiset käyrät ovat erityisen tärkeitä lukuteoriassa, ja niitä tutkitaankin nykyään aktiivisesti. Niitä käytettiin esimerkiksi Fermat'n suuren lauseen todistuksessa, ja niille on löydetty sovelluksia kryptografiasta ja kokonaislukujen tekijöihinjaosta.
Elliptinen käyrä ei ole sama asia kuin ellipsi. Nimen samankaltaisuus johtuu siitä, että molemmat käsitteet esiintyvät elliptisten integraalien yhteydessä.
Toruksen luonnollinen ryhmärakenne aiheuttaa elliptisten käyrien kummallisen geometrisen ominaisuuden. Elliptisen käyrän pisteiden joukko on Abelin ryhmä, missä pisteiden yhteenlasku on määritelty sopivasti.
Elliptiset käyrät reaalilukujen kunnassa[muokkaa | muokkaa wikitekstiä]
Vaikka elliptisen käyrän määritelmä on varsin tekninen ja vaatii esitiedoiksi algebrallista geometriaa, voidaan joitakin reaalilukujen kunnassa määriteltyjen elliptisten käyrien perusominaisuuksia kuvata lukiossa opetettavan algebran ja geometrian keinoin
Tässä kontekstissa siis kunnaksi K otetaan reaaliluvut yhteen- ja kertolaskulla varustettuna. Siis käyrät ovat muotoa
- y2 = x3 + a x + b,
missä a ja b ovat reaalilukuja. Näitä käyriä kutsutaan nimellä Weierstrassin yhtälö.
Esimerkiksi seuraavat kuvat havainnollistavat elliptisiä käyriä, joiden yhtälöt ovat y2 = x3 − x ja y2 = x3 − x + 1.
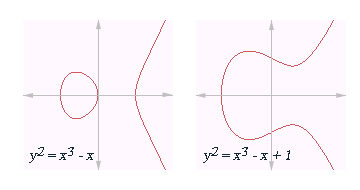
Elliptisen käyrän määritelmän perusteella käyrän tulee olla epäsingulaarinen. Geometrisesti tämä tarkoittaa sitä, että käyrällä ei ole teräviä kohtia, kuten esimerkiksi käyrällä y = x2/3 on origossa. Algebrallisesti tämä tarkoittaa sitä, että diskriminantti
- Δ = −16(4a3 + 27b2).
on nollasta poikkeava. Vaikka kerroin −16 näyttää tässä turhalta, se on kuitenkin kätevä, kun elliptisten käyrien opiskelua jatkaa pidemmälle.
Jos käyrä on ei-singulaarinen, on sen kuvaajalla kaksi komponenttia jos diskriminantti on positiivinen, ja yksi komponentti jos diskriminantti on negatiivinen. Esimerkiksi yllä olevissa kuvissa ensimmäisen käyrän diskriminantti on 64 ja jälkimmäisen −368.
Ryhmälaki[muokkaa | muokkaa wikitekstiä]
Lisäämällä käyrälle "äärettömyyspiste" saamme projektiivisen version käyrästä. Jos P ja Q ovat kaksi käyrän pistettä, löydämme yksikäsitteisesti määrätyn kolmannen pisteen käyrältä käyrän ja pisteiden P ja Q kautta kulkevan suoran leikkauspisteestä. Jos suora on tässä pisteessä käyrän tangentti, se tulee laskea mukaan kahteen kertaan. Ja jos taas suora on y-akselin suuntainen, määrittelemme pisteen olevan äärettömyydessä. Täsmälleen yksi näistä ehdoista on voimassa, kunhan elliptinen käyrä ja kaksi sen pistettä on kiinnitetty.
Nyt on mahdollista esittää käyrälle laskutoimitus "+", jolla on seuraavat ominaisuudet: Olkoon äärettömyyspiste 0, ryhmän neutraalialkio. Jos suora leikkaa käyrän pisteissä P, Q ja R, vaadimme, että P + Q + R = 0. Tästä seuraa, että ryhmä on Abelin ryhmä, ja siten Abelin varisto. Voidaan osoittaa, että K-rationaalipisteiden joukko (mukaan luettuna äärettömyyspiste) muodostaa tämän ryhmän aliryhmän. Tätä aliryhmää merkitään usein E(K).
Yllä olevaa ryhmää voidaan tarkastella sekä algebralliselta, että geometriselta kannalta. Olkoon annettu kunta K (jonka karakteristika ei ole 2 eikä 3), käyrä y2 = x3 − px − q ja käyrän pisteet P = (xP, yP) sekä Q = (xQ, yQ). Oletetaan ensiksi, että xP ≠ xQ. Olkoon s = (yP − yQ)/(xP − xQ). Koska K on kunta, s on hyvin määritelty. Tällöin voidaan määritellä R = P + Q = (xR, yR) asettamalla
Jos xP = xQ, on tällöin kaksi mahdollista vaihtoehtoa: jos yP = −yQ, on summa määritelty 0:ksi. Tällöin jokaisen pisteen inversio käyrällä löydetään peilaamalla piste x-akselin suhteen. Jos yP = yQ ≠ 0, on R = P + P = 2P = (xR, yR), joka saadaan yhtälöistä
Jos yP = yQ = 0, on P + P = 0.
Elliptiset käyrät kompleksilukujen muodostamassa kunnassa[muokkaa | muokkaa wikitekstiä]
Elliptisen käyrän esitys toruksen upotuksena projektiiviseen kompleksitasoon seuraa Weierstrassin elliptisen funktion ominaisuuksista. Nämä funktiot ja niiden ensimmäinen derivaatta ovat yhteydessä kaavan
kautta. Tässä ja ovat vakioita, on Weierstrassin elliptinen funktio ja sen derivaatta. Lausekkeesta nähdään, että tämä muoto on myös elliptinen funktio kompleksilukujen kunnassa. Weierstrassin funktiot ovat kaksoisjaksollisia. Tämä tarkoittaa sitä, että ne ovat jaksollisia lattiisin Λ suhteen. Siten Weierstrassin funktiot ovat luonnollisesti määritelty toruksen pinnalla. Tämä torus voidaan upottaa kompleksiseen projektiiviseen avaruuteen kuvauksella:
- .
Tämä kuvaus on ryhmäisomorfismi, joka vie toruksen luonnollisen ryhmärakenteen projektiiviseen avaruuteen. Se on myös Riemannin pintojen välinen isomorfisti, joten topologisessa mielessä elliptiset käyrät näyttävät toruksilta. Jos lattiisia Λ vastaa isomorfismissa lattiisi cΛ, missä c on kompleksiluku ja laskutoimitus normaali kompeksilukujen kertolasku, on vastaavat käyrät isomorfisia. Näitä isomorfismiluokkia kutsutaan j-invarianteiksi.
Isomorfismiluokat voidaan ymmärtää myös helpommalla tavalla. Vakiot ja , joita kutsutaan modulaarisiksi invarianteiksi, ovat yksikäsitteisesti määrätyt annetussa lattiisissa, eli toruksen algebrallisessa rakenteessa. Kompleksiluvut ovat kuitenkin polynomien juurikunta, joten elliptinen käyrä voidaan kirjoittaa muodossa
- .
Huomataan, että
ja
joten modulaarinen diskriminantti on
Tässä λ:a kutsutaan toisinaan modulaariseksi lambdafunktioksi.
Huomaa, että yhtenäisyyslause takaa sen, että jokainen genusta 1 oleva kompakti Riemannin pinta voidaan esittää toruksena.
Elliptiset käyrät mielivaltaisessa kunnassa[muokkaa | muokkaa wikitekstiä]
Elliptiset käyrät voidaan määritellä missä tahansa kunnassa K. Elliptisen käyrän formaali määritelmä on, että elliptinen käyrä on epäsingulaarinen projektiivinen algebrallinen käyrä K:ssa, jonka genus on 1.
Qing Liu esittää kirjassaan[1] elliptisen käyrän määritelmä seuraavasti:
Olkoon kunta. Tällöin elliptinen käyrä k:n suhteen on sileä projektiivinen käyrä yli :n, joka on isomorfinen :n suljetun alivariston kanssa, jonka määrittelee homogeeninen polynomi muotoa
yhdessä luottamuksellisen rationaalisen pisteen kanssa.
Vaikka lähteessä ei ole mainittu, on tässä kun .
Jos K:n karakteristika ei ole 2 eikä 3, voidaan jokainen elliptinen käyrä kirjoittaa muodossa
- ,
missä p ja q ovat K:n alkioita siten, että oikean puolen polynomilla x3 − px − q ei ole yhtään kaksoisjuurta. Jos K:n karakteristika on 2 tai 3, tarvitaan useampia termejä käyrää esittävään yhtälöön.
Yleensä elliptisten käyrien pisteet (x,y), jotka toteuttavat yllä olevan yhtälön ja jossa x ja y kuuluvat K:n algebralliseen sulkeumaan, ovat kiinnostavia. Näitä pisteitä kutsutaan käyrän K-rationaalisiksi pisteiksi.
Yhteydet lukuteoriaan[muokkaa | muokkaa wikitekstiä]
Mordellin-Weilin lauseen mukaan rationaalilukujen kunnassa (tai yleisemmin lukukunnassa) määritellyn elliptisen käyrän K-rationaalipisteiden muodostama ryhmä on äärellisesti viritetty Abelin ryhmä. Tämä tarkoittaa, että ryhmä voidaan esittää suorana summana vapaasta Abelin ryhmästä ja äärellisestä torsioaliryhmästä. Vaikka on suhteellisen helppoa määrittää E(K);n torsioaliryhmä, vielä ei tiedetä yleistä algoritmia jolla laskea vapaan aliryhmän aste. Birchin ja Swinnerton-Dyerin konjektuuri antaa kuitenkin kaavan jolla aste voidaan laskea, mutta otaksumaa ei ole toistaiseksi kyetty osoittamaan todeksi.
Andrew Wilesin Fermat'n suuren lauseen todistus perustui erikoistapaukseen Taniyaman–Shimuran lauseesta, joka antaa syvällisen yhteyden elliptisten käyrien ja modulimuotojen välille. Taniyaman–Shimuran lause saatiin kokonaisuudessaan todistettua vuonna 1999.
Vaikka äärellisen kunnan Fp elliptisen käyrän E rationaalipisteiden tarkka lukumäärä on vaikea selvittää, Hassen lauseen mukaan elliptisille käyrille pätee :.
Tämä fakta voidaan todistaa yleisemmän teorian avulla. Tähän tarvitaan paikallisten zeetafunktioiden teoriaa ja Étalen kohomologiaa. Annetun käyrän rationaalipisteiden lukumäärä voidaan laskea Schoofin algoritmin avulla.
Tämäntyyppisten ongelmien nykyinen tutkimus hyödyntää Abelin varistojen teoriaa.
Algoritmeja jotka hyödyntävät elliptisiä käyriä[muokkaa | muokkaa wikitekstiä]
Kryptografiassa ja kokonaislukujen tekijöihinjaossa hyödynnetään elliptisiä käyriä, jotka on määritelty äärellisissä kunnissa. Tyypillisesti äärellisessä kunnassa oleviin elliptisiin käyriin perustuvien ohjelmien idea on siinä, että niissä on algoritmit, jotka muuttavat tiettyjä äärellisiä ryhmiä elliptisten käyrien rationaalipisteiden muodostamaksi ryhmiksi. Esimerkkejä tämäntyyppisistä algoritmeista on muun muassa:
Lähteet[muokkaa | muokkaa wikitekstiä]
- ↑ Algebraic Geometry and Arithmetic Curves, Oxford Graduated Texts in Mathematics, 2006
Aiheesta muualla[muokkaa | muokkaa wikitekstiä]
- The Mathematical Atlas: 14H52 Elliptic Curves (Arkistoitu – Internet Archive)
- Wolfram Mathworld: Elliptic Curves
- James Milnen elliptisiä käyriä koskevan kurssin luentomuistiinpanot. (Arkistoitu – Internet Archive)



























