Perihelikiertymä

Perihelikiertymä eli periheliliike on ilmiö, joka tarkoittaa, että planeetan tai muun taivaankappaleen periheli eli sen radan Aurinkoa lähimpänä oleva kohta ei pysy aina samalla puolella Aurinkoa.
Merkuriuksen radan perihelikiertymä[muokkaa | muokkaa wikitekstiä]
Merkuriuksen radan perihelin kiertymä on ollut vaikeimmin selitettäviä ilmiöitä tähtitieteessä, ja sen selittämiseen on kaatunut moni uusi teoria.lähde?
Merkuriuksen radan periheli kiertyy hieman joka kierroksella. Havainnoitu liike on yli 1,5 astetta vuosisadassa.[1] 90 % tästä selittyy planeetan pyörimisakselin suunnan muutoksesta, prekessiosta. Jäljelle jäävä kiertymä on 531 kaarisekuntia vuosisadassa, eli noin 0,15 astetta. Tästä Venus aiheuttaa puolet ja muiden planeettojen aiheuttamien häiriöiden poiston jälkeen jää jäljelle 43 kaarisekunnin ylimääräinen kiertymä vuosisadassa.[1]
Ylimääräisen, selittymättömän, kiertymän syyksi arveltiin aikoinaan hypoteettista Vulkanus-planeettaa, joka oletettiin kiertävän Aurinkoa Merkuriuksen radan sisäpuolella. Kiertoratansa takia se olisi käytännössä ollut näkyvissä vain täydellisten auringonpimennysten aikana. 1800- ja 1900-lukujen vaihteessa monet tähtitieteilijät yrittivätkin etsiä sitä aina auringonpimennyksen sattuessa. Vulkanuksesta ei kuitenkaan saatu yhtään luotettavaa havaintoa.[2]
Vasta Albert Einsteinin vuonna 1916 kehittelemä yleinen suhteellisuusteoria kykeni selittämään Merkuriuksen perihelikiertymän poikkeaman ilman tuntematonta planeettaa.[1] Einstein osoitti, että jos planeetan kiertoradan isoakselin puolikas on , radan eksentrisyys e ja kiertoaika T, suhteellisuusteoreettiset ilmiöt saavat aikaan, että yhden kierroksen aikana periheli kiertyy kulman
verran (radiaaneina), missä c on valonnopeus.[3] Kun tähän sijoitetaan Merkuriuksen radan arvot: isoakselin puolikas noin 57,9 miljoonaa kilometriä eli 57,9 · 109 m, radan eksentrisyys 0,206 ja kiertoaika 87,97 d[4] eli noin 7,6 · 106 s sekä valonnopeus 3 · 108 m/s, saadaan tulokseksi = 5,028 · 10-7 radiaania, toisin sanoen noin 2,88 · 10-5 astetta eli 0,104 kaarisekuntia. Sadassa vuodessa Merkurius tekee noin 415 kierrosta, joten tästä aiheutuva kiertymä tämän pituisena aikana on noin 43 kaarisekuntia, mikä varsin tarkoin vastaa havaittua perihelikiertymän poikkeamaa.
Maan perihelikiertymä ja sen vaikutus ilmastoon[muokkaa | muokkaa wikitekstiä]
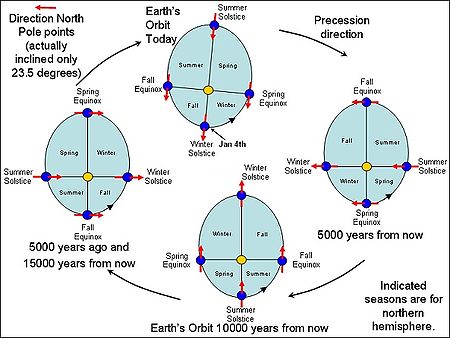
Myös Maan radan periheli kiertyy siten, että Maan perihelin argumentti kasvaa noin 0,27 astetta vuosisadassa. Kestää 134 000 vuotta, ennen kuin Maan radan periheli on jälkeen samalla puolella Aurinkoa kiintotähtien suhteen. lähde?
Samaan aikaan Maan pyörimisakseli kiertyy eli suorittaa prekessioliikettä, ja kestää noin 25 771 vuotta, ennen kuin se on jälleen samassa asennossa tähtien suhteen. Samassa ajassa ne kohdat Maan radasta, jossa Maa on tiettyinä aikoina vuodessa esimerkiksi kevät- ja syyspäiväntasauksena, tekevät täyden kierroksen Auringon ympäri. Nämä kaksi ilmiötä, perihelikiertymä ja prekessio, saavat yhdessä aikaan, että noin 21 000 vuoden välein Maa on perihelissä samaan aikaan vuodessa.[5] Nykyisin Maa on perihelissä vuosittain 4. tammikuuta, mutta 5000 vuotta sitten tämä tapahtui syyspäiväntasauksen, 5000 vuoden kuluttua kevätpäiväntasauksen aikoihin.lähde?
Näiden ilmiöiden vuoksi eri vuodenaikojen pituus vaihtelee, ja niiden arvellaan osaltaan vaikuttaneen ilmaston vaihteluihin ja esimerkiksi jääkausien syntyyn. Tämä 21 000 vuoden jakso onkin yksi ilmastonmuutosten selitykseksi esitetyistä Milankovićin jaksoista.[6]
Oheinen kaavio esittää ilmiön vaikutusta vuodenaikojen pituuksiin pohjoisella pallonpuoliskolla. Keplerin toisen lain mukaan vuodenaikojen pituudet ovat verrannollisia niitä vastaavien, radan sisäpuolelle jäävien alueiden pinta-aloihin. Kun radan eksentrisyys on suurimmillaan, ne päiväntasausten ja -seisausten mukaan määritellyt vuodenajat, jolloin Maa kulloinkin on kauimpana Auringosta, ovat merkittävästi muita vuodenaikoja pidempiä.lähde?
Lähteet[muokkaa | muokkaa wikitekstiä]
- ↑ a b c Hannu Karttunen, Heikki Oja, Pekka Kröger, Markku Poutanen: Tähtitieteen perusteet, s. 208. Tähtitieteellinen yhdistys Ursa, 1984. ISBN 951-859-367-1.
- ↑ Richard Baum ja William Sheehan: Vulkanus - suuri planeetanmetsästys. Art House, 1998. ISBN 951-884-235-3.
- ↑ Stephen Hawking: On the shoulders of giants : the great works of physics and astronomy, s. 1243, artikkeli Foundation of the General Relativity (käännös Albert Einsteinin vuonna 1916 laatimasta artikkelista Die Grundlage der Allgemeine Relativitätstheorie, alun perin julkaistu Annalen der Physikin numerossa 49). Philadelphia, Pennsylvania, USA: Running Press. ISBN 0-7624-1348-4.
- ↑ Hannu Karttunen, Heikki Oja, Pekka Kröger, Markku Poutanen: Tähtitieteen perusteet, s. 581, taulukko. Tähtitieteellinen yhdistys Ursa, Valtion painatuskeskus, 1984. ISBN 951-859-367-1.
- ↑ The Seasons and the Earth's Orbit United States Naval Observatory. Arkistoitu 2.8.2013. Viitattu 24.7.2014.
- ↑ Björn Kurtén: Jääkausi, s. 38. Suomentanut Virve Kajaste. WSOY, 1972. ISBN 951-0-00149-X.


