Geodeesi

Geodeesi eli geodeettinen viiva on ”suoran viivan” käsitteen yleistys ”kaareviin avaruuksiin”, esimerkiksi pallopinnalle tai yleisessä suhteellisuusteoriassa kaarevaan aika-avaruuteen. Geodeesin olennainen ominaisuus on, että lokaalisti (minkä tahansa pisteen pienessä ympäristössä tarkasteltuna) se muistuttaa suoraa viivaa ja (mikäli avaruudessa on olemassa etäisyysmitta) tarjoaa jossakin mielessä lyhimmän etäisyyden pisteiden välillä. Tarkka matemaattinen määritelmä vaihtelee riippuen siitä, millaista avaruutta tarkastellaan.
Geodeesi pallopinnalla[muokkaa | muokkaa wikitekstiä]
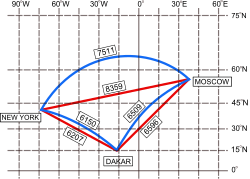
Yksinkertainen esimerkki geodeesista on pallopinnalla isoympyrä. Kahta pallopinnan pistettä yhdistävä lyhin viiva kulkee pitkin isoympyrän kaarta, joten tällainen kaari on samalla tavoin pisteiden välinen lyhin reitti tai ”suorin mahdollinen reitti” samaan tapaan kuin jana on lyhin reitti tason pisteiden välillä. Nimi geodeesi viittaa geodesiaan eli maanmittausoppiin, joka tutkii maapallon kokoa ja muotoa.[1] Esimerkiksi pitkillä meri- ja lentomatkoilla lyhin reitti kulkee pitkin isoympyrää (eikä pitkin loksodromia, joka kulkee koko ajan samaan ilmansuuntaan).
Geodeesin ja loksodromin ero voi aiheuttaa tulkintaongelmia, jos esimerkiksi sopimuksessa on sovittu jonkin rajan kulkevan maapallon pinnalla ”pitkin suoraa viivaa”. Esimerkiksi Ahvenanmaan sopimuksessa demilitarisoidun alueen rajat määriteltiin tiettyjen pisteiden välisinä ”suorina viivoina”, jolloin syntyy kysymys, tarkoitetaanko geodeeseja vai loksodromeja.[2]
Geodeesi pinnalla[muokkaa | muokkaa wikitekstiä]


Yleisemmin geodeesi voidaan määritellä millä tahansa euklidisen avaruuden alimonistolla, esimerkiksi kolmiulotteisessa avaruudessa olevalla (mahdollisesti kaarevalla) pinnalla kuten ellipsoidilla, lieriöpinnalla jne.
Vaihtoehtoisia (mutta sopivin edellytyksin yhtäpitäviä) määritelmiä ovat ainakin seuraavat:
- Geodeesi on lokaalisti etäisyyden minimoiva käyrä.[3][4] Tämä merkitsee, että jos tarkastellaan riittävän lyhyttä käyrän osaa, niin kaikkien sen pisteiden välillä lyhin reitti kulkee kyseistä käyrää pitkin. Tätä määritelmää voi havainnollistaa ajattelemalla, että pinnalle voi asettaa venytetyn kuminauhan geodeesia pitkin.[5] Jos kuminauhan yrittäisi asettaa sellaista reittiä, joka ei ole geodeesi, kuminauha pyrkisi oikaisemaan reittiä.
- Geodeesi on käyrä, jota vakiovauhdilla kuljettaessa kiihtyvyys on jatkuvasti pintaa vastaan kohtisuora.[5]
- Geodeesi on käyrä, jonka geodeettinen kaarevuus jokaisessa pisteessä on nolla. Geodeettinen kaarevuus on , missä on käyrän kaarevuus koko avaruudessa ja on käyrän binormaalin ja moniston normaalin välinen kulma.[6]
Lokaalisuuden merkitys[muokkaa | muokkaa wikitekstiä]
Usein sanotaan hiukan epätäsmällisesti, että geodeesi on tietyllä pinnalla ”kahden pisteen välinen lyhin viiva”.[7][8] Tämä on osittain totta. Mikäli kahden pisteen välillä on olemassa lyhin viiva, niin se on eräs geodeesi, mutta samojen pisteiden välillä voi olla useita eripituisia geodeeseja. Kukin geodeesi on kuitenkin lokaalisti etäisyyden minimoiva.[5]
Esimerkki 1. Jos A ja B ovat kaksi pistettä pallopinnalla lähellä toisiaan, voi niiden välillä isoympyrää pitkin kahta eri reittiä: joko ”suoraan” tai pallon ympäri. Molemmat reitit ovat geodeeseja, mutta pallon kiertävä reitti voi olla paljonkin pidempi.[5]
Esimerkki 2. Maapalloa voidaan karkeasti pitää litistyneenä ellipsoidina, jonka ympärysmitta päiväntasaajaa pitkin on 40 075 km, mutta ympärysmitta napojen kautta vain 40 008 km.[9] Jos pisteet A ja B ovat päiväntasaajalla vastakkaisilla puolilla, on niiden välimatka napojen kautta 33,5 km lyhyempi kuin päiväntasaajaa pitkin; silti molemmat reitit ovat geodeeseja.
Esimerkki 3. Lieriöpinnalla kahden pisteen välinen geodeesi (kuten kuminauha) voi kulkea mielivaltaisen monta kertaa lieriön ympäri, jolloin syntyy ruuviviiva. Tällainen viiva on lokaalisti etäisyyden minimoiva, mutta ei ole lyhin reitti pisteiden välillä.[5]
Esimerkki 4. Madonreikä (Einsteinin–Rosenin silta) on hypoteettinen oikoreitti aika-avaruudessa. Jos sellaisia esiintyy, voi samojen pisteiden välillä olla huomattavan eripituisia geodeeseja.[10]
Joillakin pinnoilla, erityisesti tasossa pätee, että kahden pisteen välillä on aina täsmälleen yksi geodeesi, joka on samalla niiden välinen lyhin viiva.[3]
Geodeesi differentiaaligeometriassa[muokkaa | muokkaa wikitekstiä]
Vielä yleisemmin geodeesi voidaan määritellä esimerkiksi millä tahansa differentioituvalla monistolla (jonka ei tarvitse olla upotettuna korkeampiulotteiseen monistoon). Jos M on differentioituva monisto ja C on sen differentioituva käyrä, niin C on geodeesi, jos sen tangenttivektorit kuljetettuna käyrää pitkin (engl. parallel displacement) pysyvät käyrän tangenttivektoreina.[11]
Lähteet[muokkaa | muokkaa wikitekstiä]
- ↑ Steven Schwartzman: The Words of Mathematics: An Etymological Dictionary of Mathematical Terms Used in English, s. 98. The Mathematical Association of America, 1994. Google Books -esikatselu (viitattu 30.10.2015).
- ↑ Ahvenanmaan demilitarisoinnin rajoja koskeva selvitys. Rajatyöryhmän mietintö (Sarjanumero 2006:18. Sivut 12, 16, 18) 2006. Oikeusministeriö. Viitattu 25.10.2015. [vanhentunut linkki]
- ↑ a b Rowland, Todd ja Weisstein, Eric W.: Geodesic MathWorld. Wolfram Research Inc.. Viitattu 25.10.2015.
- ↑ Kiyosi Itô (editor): ”178. Geodesics”, Encyclopedic Dictionary of Mathematics, s. 675. Second English edition, third printing, volume I. MIT Press.
- ↑ a b c d e John M. Sullivan: Math 302, NonEuclidean Geometry, Spring 2001 (Luentomateriaali. Kappale ”Geodesics on Smooth Surfaces”) 2001. University of Illinois at Urbana-Champaign. Viitattu 25.10.2015.
- ↑ Kiyosi Itô (editor): ”111. Differential Geometry of Curves and Surfaces”, Encyclopedic Dictionary of Mathematics, s. 418. Second English edition, third printing, volume I. MIT Press.
- ↑ Matematiikan verkkosanakirja matematiikkalehtisolmu.fi. Viitattu 25.10.2015.
- ↑ M niinkuin matematiikka. Lukiotason matematiikan tietosanakirja. Versio 1.12 (Geodeettiset viivat; pallokolmiot) matta.hut.fi. 10.08.2000. Viitattu 25.10.2015.
- ↑ Naomi E. Balaban ja James E. Bobick (toim.): The handy science answer book, s. 113. Neljäs painos. Visible Ink Press, 2011. Google Books -esikatselu (viitattu 30.10.2015).
- ↑ Leena Tähtinen: Aikamatkailu tieteellisenä ongelmana. Tieteessä tapahtuu, 2000, nro 8. Artikkelin verkkoversio. Viitattu 30.10.2015. (Arkistoitu – Internet Archive)
- ↑ Kiyosi Itô (editor): ”80. Connections”, Encyclopedic Dictionary of Mathematics, s. 303. Second English edition, third printing, volume I. MIT Press.


