Ruusukäyrä

7-terälehtinen ruusu (k = 7)

8-terälehtinen ruusu (k=4).

Yhtälön $r=\cos k\theta$ määrittämiä ruusukäyriä vakion k=n/d eri arvoilla

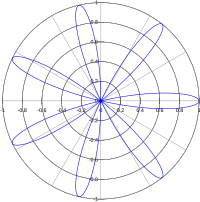
Ruusukäyrä eli Grandin ruusu (engl. Rose tai Rhodonea) on matematiikassa käyrä, jota voidaan pitää sinifunktion kuvaajana napakoordinaatistossa.

Yleiskuvaus

Jokainen ruusukäyrä on yhdenmuotoinen sellaisen käyrän kanssa, jonka yhtälö napakoordinaateissa on muotoa

$\!\,r=a\cos(k\theta )$

tai vaihtoehtoisesti

$\!\,r=a\sin(k\theta )$.

Karteesisessa koordinaatistossa käyrä voidaan edellisessä tapauksessa esittää yhtälöparilla :$\!\,x=a\cos(k\theta )\cos(\theta )$

$\!\,y=a\cos(k\theta )\sin(\theta )$.

Nimi ruusukäyrä johtuu siitä, että käyrä tyypillisesti muistuttaa muodoltaan ruusun teriötä. Jos k on kokonaisluku, tällä käyrän kuvaamalla ruusulla on

• 2k terälehteä, jos k on parillinen, ja
• k terälehteä, jos k on pariton.

Vakio a osoittaa terälehtien pituuden.

Kun k on parillinen, koko käyrä tulee piirretyksi tasan kerran, kun kulma θ kasvaa 0:sta 2π:hin. Kun k on pariton, tämä tapahtuu jo välillä 0:sta π:hin. Yleisemmin sama tapahtuu millä tahansa välillä, jonka pituus on 2π, kun k on parillinen, tai π, jos k on pariton.

Jos k on puoliluku (esimerkiksi 1/2, 3/2 tai 5/2), käyrä muistuttaa ruusua, jolla on 4k terälehteä. Esimerkiksi: n=7, d=2, k= n/d =3,5, kun θ kasvaa 0:sta 4π:hin.

Jos k voidaan esittää muodossa n±1/6, missä n on nollasta poikkeava kokonaisluku, käyrä muistuttaa ruusua, jolla on 12k terälehteä.

Jos k voidaan esittää muodossa n/3, missä n on kokonaisluku, joka ei ole jaollinen kolmella, käyrä muistuttaa muodoltaan ruusua, jolla on n terälehteä, jos n on pariton, ja 2n terälehteä, jos n on parillinen.

Jos k on rationaaliluku, käyrä on suljettu, ja sillä on äärellinen pituus. Ellei k ole kokonaisluku, terälehdet saattavat olla osittain päällekkäin. Jos k on irrationaaliluku, käyrä ei ole suljettu, ja sen pituus on ääretön. Tässä tapauksessa käyrä on lisäksi tiheä, toisin sanoen se sivuuttaa yksikkökiekon jokaisen pisteen mielivaltaisen läheltä.

Koska

$\sin(k\theta )=\cos \left(k\theta -{\frac {\pi }{2}}\right)=\cos \left(k\left(\theta -{\frac {\pi }{2k}}\right)\right)$

kaikilla $\theta$, käyrät, joiden yhtälöt napakoordinaateissa ovat

$\,r=\sin(k\theta )$ and $\,r=\cos(k\theta )$

ovat yhtenevät ja voidaan kuvata toisilleen π/2k radiaanin rotaatiolla.

Ruusukäyrille antoi nimen italialainen matemaatikko Guido Grandi vuosien 1723 ja 1728 välillä.

Eräs ruusukäyrän erikoistapaus on neliapilan muotoinen käyrä, jolla k = 2. Sillä on karteesisissa koordinaateissa myös yhtälö

$(x^{2}+y^{2})^{3}=4a^{2}x^{2}y^{2}$

Pinta-ala

Ruusukäyrän

$r=a\cos(k\theta )\,$,

sisään jäävän alueen eli terälehtien yhteenlaskettu pinta-ala on

${\frac {1}{2}}\int _{0}^{2\pi }(a\cos(k\theta ))^{2}\,d\theta ={\frac {a^{2}}{2}}\left(\pi +{\frac {\sin(4k\pi )}{4k}}\right)={\frac {\pi a^{2}}{2}}$

jos k on parillinen, ja

${\frac {1}{2}}\int _{0}^{\pi }(a\cos(k\theta ))^{2}\,d\theta ={\frac {a^{2}}{2}}\left({\frac {\pi }{2}}+{\frac {\sin(2k\pi )}{4k}}\right)={\frac {\pi a^{2}}{4}}$

jos k on pariton positiivinen kokonaisluku.

Sama pätee ruusukäyrille, joiden yhtälö napakoordinaateissa on

$r=a\sin(k\theta )\,$

sillä tämän yhtälön kuvaaja saadaan kosinin avulla määritellystä ruusukäyrästä yksinkertaisella rotaatiolla.

Muodon riippuvuus parametrista k

Ruusukäyrän napakoordinaateissa esitetyssä yhtälössä esiintyy vakiotekijä k. Kun k on kokonaisluku, käyrä muodostaa muodoltaan kukkaa. Sillä on k terälehteä, jos k on pariton, ja 2k terälehteä, jos k on parillinen. Sen sijaan millään vakion k arvolla ei saada aikaan sellaista kukkaa, jossa terälehtien lukumäärä on parillinen mutta ei neljällä jaollinen (esimerkiksi 2, 6, 10 tai 14).

Kun d on alkuluku, on n/d supistumaton murtoluku. Kun ruusukäyrän yhtälössä oleva k on tällainen murtoluku, käyrän terälehden ovat osittain päällekkäin. Niiden terälehtien lukumäärä, joiden kanssa kukin niistä on osittain päällekkäin, on yhtä suuri kuin järjestysluku, joka ilmoittaa, kuinka mones alkuluku d on alkulukujen jonossa, kun luku 1 lasketaan mukaan (esimerkiksi kun d on 2, tämä luku on 2, ja vastaavasti alkulukuja 3, 5 ja 7 vastaavat lukumäärät 3, 4 ja 5).

Kun k on muotoa k = 1/d, missä d on parillinen, käyrä muodostaa sarjan sisäkkäisiä silmukoita, ja keskellä on kaksi pienintä silmukkaa, jotka sivuavat toisiaa origossa. Käyrä on symmetrinen x-akselin suhteen. Jos taas d on pariton, käyrä muodostaa d div 2 sisäkkäistä silmukkaa, joista pienin sivuaa origoa joko vasemmalla (kun d on muotoa d = 4n − 1) tai oikealla ((kun d on muotoa d = 4n + 1).0

Jos d ei ole alkuluku eikä n ole 1, käyrän muodostaa sarja toisensa leikkaavia silmukoita.

Jos k on irrationaaliluku, ruusukäyrällä on äärettömän monta terälehteä, ja se on tiheä yksikkökiekossa.

• Esimerkkejä hammasrattailla muodostettavista ruusukäyristä eri suhdeluvuilla
• 
  n=1, d=1, k=1
• 
  n=1, d=3, k≈0.333
• 
  n=3, d=1, k=3
• 
  n=4, d=5, k=0.8

Lähteet

• Rose Wolfram MathWorld. Viitattu 8.9.2017.

Aiheesta muualla

• Kuvia tai muita tiedostoja aiheesta Ruusukäyrä Wikimedia Commonsissa