Rotaatio (geometria)
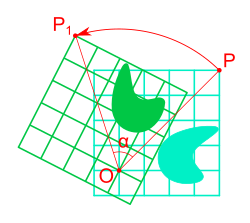
Geometriassa rotaatio eli kierto on eräs yhtenevyyskuvaus. Siinä tasokuvio kierretään jonkin kiinteän pisteen ympäri taikka kolmiulotteisen avaruuden kappaleet jonkin akselin ympäri siten, että jokaisen pisteen vastinpiste kuvauksessa on samalla etäisyydellä tästä kiinteästä pisteestä tai akselista kuin alkuperäinen piste, mutta eri suunnassa.
Kierto tasossa[muokkaa | muokkaa wikitekstiä]


Tasossa rotaation määrittämiseen riittää piste, jonka ympäri se suoritetaan, sekä kulma, jonka verran tasoa kierretään, eli kiertokulma. Annetun pisteen vastinpisteen laskemiseen voidaan käyttää matriisilaskentaa tai kompleksilukuja. Kummassakin tapauksessa piste, jonka ympäri kierretään, voidaan valita origoksi ja sopia, että kulma θ osoittaa, minkä verran tasoa kierretään vastapäivään.
Jos kulma θ on 180 astetta, rotaatio tasossa pisteen ympäri vastaa peilausta tämän pisteen suhteen.
Matriisilaskenta[muokkaa | muokkaa wikitekstiä]
Kutakin tason pistettä (x, y) vastaa tietty paikkavektori. Tason kiertoa origon ympäri vastaa tietty matriisi, jolla tämä paikkavektori kerrotaan. Jos kiertokulma on , tämä matriisi voidaan esittää muodossa
- .
missä (x′, y′) ovat pisteen koordinaatit rotaation jälkeen. Nämä voidaan laskea alkuperäisten koordinaattien (x, y) avulla seuraavasti:
Vektorit ja ovat yhtä pitkät eli itseisarvoltaan yhtä suuret, ja niiden välinen kulma on .
Kompleksiluvut[muokkaa | muokkaa wikitekstiä]
Tasoa voidaan käsitellä myös kompleksitasona. Tällöin tason jokaista pistettä (x, y) vastaa kompleksiluku
Tason kiertoa kulman θ verran vastaa jokaisen kompleksiluvun kertominen vakiolla
- eiθ,
joka Eulerin kaavan mukaan on sama kuin
Tätä muotoa olevien kompleksilukujen itseisarvo on 1. Täten saadaan:
mikä johtaa samaan tulokseen kuin matriisienkin avulla:
Erityisesti kompleksiluvin kertominen imaginaariyksiköllä i vastaa tason kiertoa 90 astetta vastapäivään ja kertominen -i:llä kiertoa 90 astetta myötäpäivään.
Kompelksilukujen kertolasku on kommutatiivinen, ja sen mukaisesti ovat tason rotaatiotkin, toisin kuin korkeammissa ulottuvuuksissa. Toisin sanoen jos tasossa suoritetaan useampi rotaatio origon ympäri, lopputulos on riippumaton siitä, missä järjestyksessä ne on suoritettu. Rotaatioon liittyy vain yksi vapausaste, koska kiertokulma määrittää sen yksikäsitteisesti.[1]
Kertominen kompleksiluvulla, jonka itseisarvo ei ole 1, ei vastaa rotaatiota vaan jotakin sellaista yhdenmuotoisuuskuvausta, jossa myös kuvioiden koko muuttuu.
Kolmiulotteisen avaruuden rotaatio[muokkaa | muokkaa wikitekstiä]
Kolmiulotteisen euklidisen avaruuden rotaatio eroaa useilla merkittävillä tavoilla vastaavasta kuvauksesta tasosta. Rotaatiot eivät yleensä ole kommutatiivisia, eli jos suoritetaan useampi rotaatio, lopputulos riippuu siitä, missä järjestyksessä ne on suoritettu. Rotaatiolla on lisäksi kolme vapausastetta eli yhtä monta kuin ulottuvuuttakin.
Matriisilaskenta[muokkaa | muokkaa wikitekstiä]
Kolmiulotteisessa avaruudessakin pisteitä voidaan kuvata paikkavektorilla (x, y, z ja rotaatioita origon ympäri matriisilla, jolla kertomalla tämä piste kuvautuu pisteeksi (x′, y′, z′). Tarvittava matriisi on 3 × 3 -matriisi,
Kun vektori kerrotaan tällä, saadaan
Tämä matriisi A kuuluu ryhmään SO(3), ja sen on oltava ortogonaalinen matriisi, jonka determinantti on 1. Matriisin ortogonaalisuus merkitsee, että sen rivit vastaavat keskenään kohtisuoria yksikkövektoreita. Tällaisen matriisin determinantti voi olla +1 tai -1, mutta jos se on -1, se ei vastaa rotaatiota vaan peilausta jonkin tason suhteen.
| Tämä artikkeli tai sen osa on tuotu vieraskielisestä lähteestä ja käännös on keskeneräinen. Voit auttaa Wikipediaa tekemällä käännöksen loppuun. |
Kvaterniot[muokkaa | muokkaa wikitekstiä]
Kolmiulotteisen avaruuden rotaatiota voidaan vaihtoehtoisesti käsitellä myös kvaternioiden avulla. Kvaterniot ovat muotoa w + xi + yj + xk olevia lausekkeita, joissa w, x, y ja z ovat reaalilukuja, i, j ja k sellaisia lukuja, joiden kaikkien neliö on -1. Kompleksilukujen tavoin myös kvaternioille voidaan määritellä yhteen- ja kertolasku, mutta toisin kuin reaali- ja kompleksiluvuilla, niiden kertolasku ei ole kommutatiivinen.
Kvaternioita käytettäessä kutakin avaruuden pistettä (x, y, z) vastaa kvaternio xi + yj + zk. Avaruuden rotaatiot vastaavat tällöin sellaisia kvaternioita, joiden itseisarvo on 1 eli Tällöin on kuitenkin suoritettava kaksi kertolaskua. Piste, jota vastaava kvaternio on x, kuvautuu pisteeksi
missä q on rotaatiota vastaava kvaternio ja q-1 sen käänteisarvo.
Lähteet[muokkaa | muokkaa wikitekstiä]
- Hestenes, David (1999). New Foundations for Classical Mechanics. Dordrecht: Kluwer Academic Publishers. ISBN 0-7923-5514-8.
- Lounesto, Pertti (2001). Clifford algebras and spinors. Cambridge: Cambridge University Press. ISBN 978-0-521-00551-7.
Viitteet[muokkaa | muokkaa wikitekstiä]
- ↑ Lounesto 2001, s. 30.
Kirjallisuutta[muokkaa | muokkaa wikitekstiä]
- Kivelä, Simo K.: Matriisilasku ja lineaarialgebra. Helsinki: Otatieto, 1984. ISBN 951-671-368-8.
- Pitkäranta, Juhani: Calculus Fennicus – TKK:n 1. lukuvuoden laaja matematiikka (2000–2013) (pdf) Helsinki: Avoimet oppimateriaalit ry. ISBN 978-952-7010-12-9 ISBN 978-952-7010-6 (pdf). Viitattu 8.7.2019.












