Painopiste (geometria)
Geometrisellä painopisteellä tarkoitetaan tasokuvion tai avaruuskappaleen tasapainokohtaa, jossa se olisi fysikaalisena esineenä tasapainossa fysikaalisen painopisteensä suhteen. Luonnollisten kappaleiden painopisteiden määritykseen käytetään kokeellisia menetelmiä, kuten esimerkiksi painopistevaakaa, mutta yksinkertaisten ja säännöllisten kuvioiden painopisteen etsimiseen käytetään geometrian keinoja. Perusajatus on, että geometriset kuviot ovat ideaaleja ja muistuttavat todellisia materiaaliltaan homogeenisia kappaleita.[1]
Tasainen painovoima vaikuttaa painopisteeseen kuin sen koko massa olisi keskittynyt siihen, mistä syystä sitä kutsutaan myös massakeskipisteeksi. Mikäli painovoimakenttä vaihtelee kappaleen kohdalla, voi painopiste sijaita eri kohdassa kuin massakeskipiste.[2]
Levymäisen kappaleen painopiste voidaan määrittää ripustamalla se jostakin kohtaan lankaan, jolloin painopiste sijaitsee langan jatkeella. Jos langan asento piirretään levylle ja ripustetaan levy toisesta kohtaa langalla, saadaan langan ja viivan leikkauspisteestä selville levyn painopiste. Kolmiulotteisen kappaleen painopiste löydetään kolmen leikkaavan tason leikkauspisteessä.[1][3][2]
-
Levymäinen kappale, jonka painopiste määritetään.
-
Ensimmäinen ripustaminen ja viivan piirto.
-
Toinen ripustaminen ja langan ja viivan leikkauspiste. Painopiste sijaitsee täplän kohdalla.
-
Kolmiulotteisen kappaleen painopiste sijaitsee kolmen ripustustason leikkauspisteessä.
Fysikaalinen ja matemaattinen perusta[muokkaa | muokkaa wikitekstiä]
Painopisteen koordinaatit määritetään mekaniikassa tasapainoyhtälöillä. Niissä huomioidaan kappaleen geometrian lisäksi myös aineen tiheysvaihtelut. Geometrisissä menetelmissä oletetaan kappale olevan homogeeninen eli että sen tiheys ei vaihtele kappaleen eri osissa. Silloin painopisteen paikka riippuu vain kappaleen geometriasta.[2]
Tasoalue tai avaruuskappale[muokkaa | muokkaa wikitekstiä]
Geometrisessa tarkastelussa voidaan olettaa, että kappale on tiheydeltään homogeeninen (). Silloin kappaleen "atomien" massa ja niiden tilavuus ovat verrannolliset, jolloin riittää tarkastella pelkästään pinta-aloja tai tilavuuksia. Kappaleen kokonaismassan arvo voidaan korvata pinta-alan arvolla
tai tilavuuden arvolla
Itse painopiste lasketaan tilan paikkavektoreilla fysikaalisen periaatteen mukaisesti
Jos kappaleen tiheys on sama joka pisteessä, ovat massat kaikki samansuuruiset ja niiden vaikutukset kumoutuvat, jolloin tulos riippuu vain geometriasta.
Lauseke voidaan myös esittää muodossa
missä integraalit otetaan koko tason tai avaruuden yli ja missä g on tasoalueen tai kappaleen karakteristinen funktio, jonka arvo on 1 alueen tai kappaleen sisällä ja 0 sen ulkopuolella.[5] Tämän lauseen nimittäjä on sama kuin tasoalueen pinta-ala tai kappaleen tilavuus.
Jos integroitavia pisteitä on vähän, voidaan samat laskut suorittaa summillakin. Tasokuvion painopiste on silloin kaikkien kuvion pisteiden aritmeettinen keskiarvo koordinaatin suhteen. Tämä lasketaan karteesisessa koordinaatistossa x-koordinaattien keskiarvona, y-koordinaattien keskiarvona ja z-koordinaattien keskiarvona, eli
ja
ja
Pistemäisten massojen joukko[muokkaa | muokkaa wikitekstiä]
Mekaniikassa voidaan johtaa momentin käsitteen avulla pistemäisten kappaleiden yhteiselle painopisteelle paikan lauseke. Samaa kaavaa voidaan käyttää integraalin sijasta, jos jakaa kappaleen mosaiikiksi, joiden keskipisteet ja massat sijoitetaan kaavaan. Tuloksena saadaan painopisteen likimääräinen paikka.[6][2]
Mikäli eripainoisia pisteitä on paljon , voidaan painopiste laskea yleisesti näiden painotettuna keskiarvona:
Jos massat ovat kaikki samanpainoisia, saadaan painopisteeksi
Viimeinen lauseke voidaan tulkita pisteiden koordinaattien keskiarvoksi.[4]
Eräitä painopisteen paikan päättelysääntöjä[muokkaa | muokkaa wikitekstiä]
Arkhimedeen lemma[muokkaa | muokkaa wikitekstiä]
Jo Arkhimedes (287−212 eaa.) muotoili käytännöllisen geometrisen tavan löytää painopiste:
- Jos kappale jaetaan kahteen pienempään osaan, sijaitsee kappaleen alkuperäinen painopiste janalla, joka yhdistää pienempien osien painopisteet.[3]
Jos merkitään painopisteet ja massat ja , voidaan tämä lemma voidaan pukea eksaktiksi lausekkeeksi, jossa painopisteen paikkakin on määritelty
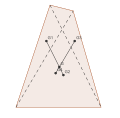
L-muotoisen levymäisen kuvion painopiste voidaan löytää Arkhimedeen lemman avulla, kun jaetaan kuvio kahdelle eri tavalla kahdeksi suorakulmioksi. Suorakulmion keskipisteet ovat painopisteet, joiden välisellä janalla kuvion painopiste on. Erilainen jako suorakulmioihin muuttaa painopisteiden paikkoja, joten toinen jana risteää ensimmäistä janaa. Koska kuvion painopiste sijaitsee kummallakin janalla samanaikaisesti, on sen paikka oltava janojen leikkauspisteessä.[3]
-
Arkhimedeen lemma: L-muotoisen tasokuvion kahden osan painopisteet yhdistettynä janalla.
-
Edellisen janan lisäksi muodostetaan toinen jana jakamalla L-muotoinen tasokuvio eri tavalla osiin. Janat leikkaavat painopisteessä, joka kuuluu molemmille janoille.
Symmetrian ja siirron vaikutus painopisteeseen[muokkaa | muokkaa wikitekstiä]
Seuraavat päättelysäännöt on merkitty tunnuksilla, jotta niihin voidaan jälkeenpäin viitata:
- (S1) Jos tasokuviolla on symmetriapiste, sijaitsee painopiste symmetriapisteessä eli keskipisteessä.[3] Tällaisia kuvioita ovat esimerkiksi ympyrä, neliö ja muut säännölliset monikulmiot.
- (S2) Jos tasokuviolla on symmetria-akseli, sijaitsee painopiste jossakin symmetria-akselin pisteessä.[3] Jo kahden symmetria-akselin olemassaolo kiinnittää painopisteen paikan. Tällaisia ovat esimerkiksi tasakylkiset kolmiot, suorakulmiot, suunnikkaat, tasakylkiset puolisuunnikkaat, sektorit, ellipsit ja katkaistut paraabelit.
- (S3) Jos tasokuvio siirretään annetulla vektorilla uuteen paikkaan, siirtyy painopiste samalla vektorilla osoitettavaan paikkaan.[3]
- (S4) Jos tasokuvio kierretään annetun kiertopisteen ympäri annetun kiertokulman verran, siirtyy myös painopiste samalla tavalla osoitettuun paikkaan.[3]
-
Tasakylkisen kolmion painopiste sijaitsee jossakin kohtaa symmetria-akselilla.
-
Neliöllä on 4 symmetria-akselia, jotka leikkaavat neliön keskipisteessä.
-
Kuusikulmiolla on 12 symmetria-akselia, jotka leikkaavat yhdessä pisteessä. Tämä piste on samalla säännöllisen monikulmion painopiste.
Pistejoukon painopiste[muokkaa | muokkaa wikitekstiä]

Kahden erimassaisen pisteen painopiste[muokkaa | muokkaa wikitekstiä]
Aristoteles (384−322 eaa.) totesi, aikalaistensa tavoin, että tangon ja sen päissä olevat painot saadaan tasapainoon sijoittamalla tukipiste kohtaan, jonka etäisyydet painoihin ovat kääntäen verrannolliset käytettyihin massoihin.[8] Nykymerkinnöin etäisyydet massojen ja kolmiulotteiset paikat ovat ja , jolloin antiikin sääntö väittää etäisyydet tukipisteeseen eli painopisteeseen ovat . Tukipiste sijaitsee :stä katsoen
eli
Tämä laskusääntö on sama kuin kahden erillään sijaitsevan fysikaalinen massapisteen yhteinen painopiste.
Kahden massan painopisteen määrittelyssä voidaan hyödyntää geometrisia ominaisuuksia (katso kuva). Kolmiossa kulmanpuolittajan jakaa kolmion vastaisen sivun viereisten sivujen suhteessa. Täydentämällä massoja pitelevään tankoon kolmion puuttuvat kaksi sivua siten, että sivujen pituudet ovat käänteisessä suhteessa massoihin, löydetään painopiste kulmanpuolittajan avulla.
Kahden samamassaisen pisteen painopiste saadaan merkitsemällä ja kun massat supistetaan pois jää lausekkeeksi
Kolmen samamassaisen pisteen painopiste[muokkaa | muokkaa wikitekstiä]
Kolme pistettä sijaitsevat aina samalla tasolla muodostaen kolmion kärkipisteet (tai kollineaarisina janan). Kolmen pisteen painopiste voidaan päätellä käyttäen myöhemmin kuvattua Archimedeen lemmaa. Kahden samamassaisen pisteen painopiste sijaitsee pisteiden keskipisteessä. Keskipisteen ja kolmannen pisteen painopiste sijaitsee niitä yhdistävällä janalla . Valitsemalla kaksi pistettä ja yhdistämällä niiden painopiste kolmannen pisteen kanssa janalla , leikkaavat janat ja pisteessä . Myös kolmas tällä tavalla muodostettu jana leikkaa kaksi muuta samassa pisteessä . Janat ovat "kolmion" keskijanoja ja ne leikkaavat toisensa kolmion painopisteessä, joka on eräs kolmion merkillinen piste. Siis kolmiolevyn ja kolmion kärkien massan painopisteet ovat samassa paikassa.[3]
Usean samamassaisen pisteen painopiste[muokkaa | muokkaa wikitekstiä]
Äärellisen pistejoukon painopisteen koordinaatit esitetään määritelmän mukaisesti kunkin samanpainoisen pisteen koordinaattien aritmeettisena keskiarvona. Kun pisteitä on kappaletta , kun , on painopisteen paikka
Painopiste minimoi sen ja pistejoukon pisteiden välisten (euklidisen) etäisyyksien neliöiden summan.
Painopisteen etsiminen vektorisumman avulla[muokkaa | muokkaa wikitekstiä]

Pistejoukon painopisteen etsimiseen voidaan käyttää vektorimatematiikkaa. Arvataan ensin painopisteen likimääräinen paikka ja piirretään siitä vektorit ympäröiviin pisteisiin. Lasketaan vektorien vektorisumma ja jos se on nolla, on painopiste oikealla paikalla . Ellei se ole vielä nolla, siirretään piste uuteen paikkaan ja tarkistetaan vektorisumma. Näin jatketaan kunnes painopiste saavutetaan riittävällä tarkkuudella.[7]
Janojen painopiste[muokkaa | muokkaa wikitekstiä]
Janan painopiste[muokkaa | muokkaa wikitekstiä]
Janan AB pisteet voidaan esittää päätepisteiden ja avulla muodossa
- , kun
Integroimalla janan pisteet :n suhteen, saadaan
Viimeinen lauseke tarkoittaa janan päätepisteiden koordinaattien keskiarvoa. Geometrisesti ajatellen janan painopiste G löytyy janan keskipisteessä.
Kahden janan painopiste[muokkaa | muokkaa wikitekstiä]
Yhdistetään kaksi yhtäpitkää janaa toisiinsa toisesta päätepisteestään. Riippumatta janojen välisestä kulmasta, janat muodostavat symmetrisen kuvion. Painopiste sijaitsee tällä symmetria-akselilla. Toisaalta, Arkhimedeen lemmasta seuraa uusi jana, jossa janojen painopisteinä olevat keskipisteet yhdistetään toisiinsa. Yhdysjana ja symmetria-akseli leikkaavat kuvion painopisteessä.[3]
Kahden eripitkän janan kuviolla ei ole symmetria-akselia. Janojen keskipisteet voidaan kuitenkin yhdistää janalla. Painopiste sijaitsee yhdysjanalla. Jakamalla pitempi jana lyhyemmän janan kanssa yhtäpitkään osaan ja loppupätkään, voidaan painopiste löytää. Katkaistulla kuviolla on nyt symmetria-akseli ja sen painopiste löydetään edellisen esimerkin mukaisesti. Koska loppupätkä on jana, on sen painopiste pätkän keskipisteessä. Yhdistämällä keskipiste ja symmetrisen kuvion painopiste janalla, leikkaa jana yhdysjanan kuvion painopisteessä.[3]
Kolmioksi yhdistettyjen kolmen janan painopiste[muokkaa | muokkaa wikitekstiä]
Yhdistetään kolme janaa kolmion muotoon, jolloin koko kuvion massa sijaitsee vain kolmion reunassa. Tällaisen kehikon painopiste sijaitsee kolmion Spiekerin pisteessä. Spiekerin piste on eräs kolmion merkillinen piste.[9]
Tasokuviot[muokkaa | muokkaa wikitekstiä]
Kolmio[muokkaa | muokkaa wikitekstiä]
Kolmion painopiste löytyy helposti piirtämällä kolmion kulmista vastaisille sivuille keskijanat. Kolmion painopiste löytyy keskijanojen eli mediaanien leikkauspisteestä.
Kun tunnetaan kolmion kärkien A, B ja C koordinaatit, voidaan painopiste laskea keskiarvon avulla
- .
Painopisteen barysentriset koordinaatit ovat
-
Kolmion painopisteen löytäminen keskijanojen avulla.
-
Painopiste sijaitsee myös korkeussuunnassa -korkeudella eri sivuista.
-
Vinojen kolmioiden painopiste sijaitsee keskijanalla ja siinä -korkeudella.
Nelikulmio[muokkaa | muokkaa wikitekstiä]
Neliöllä, jonka sivun pituus on , on neljä symmetria-akselia, jotka leikkaavat neliön keskipisteessä. Keskipiste onkin neliön painopiste (ed. symmetriasääntö S1), jonka koordinaatit ovat neliö vasemmasta kulmasta lukien . Keskipisteen löytää piirtämällä viivaimella neliölle molemmat lävistäjät, joiden leikkauspisteessä se on.
Suorakulmiolla, jonka leveys on ja korkeus , on kaksi symmetria-akselia, joten sen painopiste sijaitsee niiden leikkauspisteessä eli keskipisteessä (symmetriasääntö S1). Painopiste koordinaatit ovat vasemmasta kulmasta lukien . Keskipisteen löytää piirtämällä viivaimella suorakulmiolle molemmat lävistäjät, joiden leikkauspisteessä se on.
Suunnikkaan painopiste on molempien lävistäjien puolessa välissä sijaitsevassa leikkauspisteessä. Jos vaakasivun pituus on ja toisen sivun pituus ja joiden välinen terävä kulma on , ovat painopisteen koordinaatit [10]
Puolisuunnikkaassa on kaksi yhdensuuntaista sivua ja ehdolla , joiden korkeusero on . Mikäli kyljet ovat yhtä pitkät, puhutaan tasakylkisestä puolisuunnikkaasta. Tasakylkisellä puolisuunnikkaalla on vain yksi symmetria-akseli, joka yhdistää yhdesuuntaisten sivujen keskipisteet. Painopiste sijaitsee tällä akselilla kohdassa [10] Yleisessä puolisuunnikkaassa painopiste sijaitsee pisteessä [11] missä sivut ja ovat puolisuunnikkaan kyljet. Lävistäjien leikkauspiste tulee liian ylös ollakseen painopisteessä.
Konveksissa nelikulmiossa lävistäjät leikkaavat toisensa nelikulmion sisällä.Sen painopiste voidaan löytää jakamalla se kolmioiksi kahdella tavalla. Ensimmäisen jaon kolmioiden painopisteet yhdistetään janalla, jolla leikataan toisen jaon vastaavalla janalla. Arkhimedeen lemman mukaan, painopiste sijaitsee leikkauskohdassa.
-
Kahden symmetria-akselin leikkauspiste on suorakulmiossa painopiste.
-
Yleisen puolisuunnikkaan painopiste sijaitsee yhdensuuntaisten sivujen bimediaanisella janalla.
-
Nelikulmion lävistäjät jakavat sen kahdeksi kolmioksi kahdella tavalla. Kolmioparin painopisteet yhdistävä jana leikkaa toisen vastavalla tavalla muodostetun janan painopisteessä.
Lähteet[muokkaa | muokkaa wikitekstiä]
- ↑ a b c Simons, Lennart: Fysiikka korkeakouluja varten, s.32
- ↑ a b c d e f Lehto, Heikki et al.: Fysiikka 5, s. 61–65. (lukion fysiikan oppikirja). Helsinki: Tammi, 2010. ISBN 978-951-31-5296-3.
- ↑ a b c d e f g h i j k l Apostol, Tom, M. & Mnatsakanian, Mamikon, A.: Finding Centroids the Easy Way. Math Horizons, 2000, 8. vsk, nro 1. Mathematical Assosiation of America. ISSN 10724117. Artikkelin verkkoversio (pdf). Viitattu 10.9.2013. (englanniksi)
- ↑ a b c d e f g Weisstein, Eric W.: Geometric Centroid (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)
- ↑ Protter, Murray H.; Morrey, Jr., Charles B.: College Calculus with Analytic Geometry (2nd ed.). Reading: Addison-Wesley,, 1970.
- ↑ a b Seppänen, Raimo et al.: MAOL, s. 118. (lukion taulukkokirja, keltainen). Helsinki: Otava, 2005. ISBN 978-951-1-20607-1.
- ↑ a b Apostol, Tom, M. & Mnatsakanian, Mamikon, A.: Centroids Constructed Graphically. Mathematics Magazine, 2004, 77. vsk, nro 3, s. 201–210. Mathematical Assosiation of America. ISSN 0025570X. Artikkelin verkkoversio (pdf). Viitattu 10.9.2013. (englanniksi)
- ↑ Boyer, Carl B. & Merzbach, Uta C.: Tieteiden kuningatar – Matematiikan historia, osa I, s. 184–185. Suomentanut Kimmo Pietiläinen. Helsinki: Art House, 1994. ISBN 951-884-150-0.
- ↑ Weisstein, Eric W.: Spieker Center (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)
- ↑ a b Beardmore, Roy: Properties of plane Shapes
- ↑ Weisstein, Eric W.: Trapezoid (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)
























































![{\displaystyle \lambda \in [0,1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/92acf831876f82660dd15cb63c2efadcc2d805fd)