Meritiede
Siirry navigaatioon
Siirry hakuun
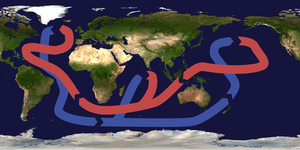
Meritiede[1] eli oseanografia (kreikan okeanos, maailmaa ympäröinyt meri) pyrkii ymmärtämään ja kvantitatiivisesti ennustamaan merten ilmiöitä. Meret ovat vesimassa, joka peittää noin kaksi kolmasosaa maapallon pinnasta. Meritiede on monitieteinen ala. Merten ilmiöiden selittäminen vaatii usein sekä fysikaalista, kemiallista että biologista tarkastelua. Yleensä meritiede jaetaan fysikaaliseen, kemialliseen, biologiseen, meteorologiseen ja geologiseen meritieteeseen.
Meritieteen osa-alueita:
Vesi ympäristössä
Vettä tutkivat tieteet
Aiheeseen liittyvää
Lähteet[muokkaa | muokkaa wikitekstiä]
Aiheesta muualla[muokkaa | muokkaa wikitekstiä]
 Kuvia tai muita tiedostoja aiheesta Meritiede Wikimedia Commonsissa
Kuvia tai muita tiedostoja aiheesta Meritiede Wikimedia Commonsissa
Kirjallisuutta[muokkaa | muokkaa wikitekstiä]
- Myrberg, Kai & Leppäranta, Matti: Meret: Maapallon siniset kasvot. Helsinki: Ursa, 2014. ISBN 978-952-5985-20-7.
