Traktrix

Traktrix, joka syntyy, kun langan toista päätä ensin työnnetään ja sitten vedetään vakionopeudella.

Traktrix eli traktriks on geometrinen käyrä, jota pitkin vedettävä kappale etenee, kun se on kiinnitetty venymättömän langan toiseen päähän, ja langan toisessa päässä oleva vetäjä etenee suoraa pitkin tasaisella nopeudella siten, että alkutilanteessa lanka on kohtisuorassa mainittuun suoraan nähden ja kappaleen liikesuunta on koko ajan suoraan kohti vetäjää. Näin ollen käyrän jokaisesta tangentista jää yhtä pitkä osa sivuamispisteen ja käyrän asymptoorin väliin. Käyrää tutki ensimmäisenä Claude Perrault vuonna 1670, myöhemmin tarkemmin Isaac Newton 1676 ja Christiaan Huygens 1693. Käyrän nimi johtuu latinan verbistä trahere, joka tarkoittaa "vetää".

Matemaattinen johto

Alun perin pisteessä (4,0) sijainneen kappaleen traktrix.

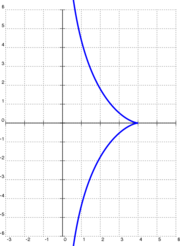
Seuraavassa tarkastellaan traktrixia, jolla on pystysuorana asymptoottina y-akseli.

Oletetaan, että kappale sijaitsee aluksi pisteessä (a, 0)), tai kuten oheisen kuvan esimerkissä, pisteessä (4,0) ja että se on kiinnitetty lankaan, jonka pituus on a (esimerkkitapauksessa 4), jonka toinen pää on origossa. Oletetaan, että langan toista päätä aletaan vetää y-akselin positiiviseen suuntaan vakionopeudella. Joka hetki tämä lanka on sen käyrän y = y(x) tangentti, jota pitkin kappale liikkuu, minkä vuoksi vetäjän liike määrää täysin myös vedettävän kappaleen liikkeen. Jos kappaleen koordinaatit jollakin hetkellä ovat (x, y), vetäjän y-koordinaatti on Pythagoraan lauseen mukaisesti $y+\operatorname {sign} (y){\sqrt {a^{2}-x^{2}}},$. Koska langan ja x-akselin välinen kulma on sama kuin ratakäyrän tangentin, saadaan differentiaaliyhtälö

${\frac {dy}{dx}}=\pm {\frac {\sqrt {a^{2}-x^{2}}}{x}}$

missä reunaehtona on, että y(a) = 0. Yhtälön ratkaisu on

$y=\int _{x}^{a}{\frac {\sqrt {a^{2}-t^{2}}}{t}}\,dt=\pm \!\left(a\ln {\frac {a+{\sqrt {a^{2}-x^{2}}}}{x}}-{\sqrt {a^{2}-x^{2}}}\right),$

missä etumerkki $\pm$ riippuu vetäjän liikesuunnasta: liikkuuko se ylös- vai alaspäin.

Lausekkeen ensimmäinen termi voidaan kirjoittaa myös muotoon

$y\operatorname {arsech} {\frac {x}{a}},$

missä arsech tarkoittaa areahyperbelisekanttia.

Ratkaisun etumerkki riippuu siis siitä, liikkuuko vetäjä ylös- vai alaspäin. Molemmat haarat kuuluvat traktrix-käyrään, jolla on terävä kärki pisteessä (a, 0).

Traktrixin merkitys

Traktrixin oleellisin ominaisuus on, että käyrällä olevan pisteen P ja sen kautta kulkevan tangentin ja käyrän asymptootin leikkauspisteen välinen etäisyys on vakio.

Traktrix voidaan käsittää monella tavalla:

1. Se on hyperbolisen spiraalin keskipisteen ura, kun tämä käyrä vierii liukumatta suoraa pitkin.
2. Ketjuviivan evolventti on traktrix, jonka asymptootti on vaakasuora. Ketjuviiva on käyrä, jonka muotoiseksi täysin taipuisa ketju köysi asettuu painovoiman vaikutuksesta, kun se on kiinnitetty kahteen tukipisteeseen. Tämän käyrän yhtälö on $y=a\cosh {\frac {x}{a}}$.
3. Jos auto on luisunut suoran tien ulkopuolelle kohtisuorasti tiehen nähden, mistä sitä lähdetään vetämään hinausautolla, joka liikkuu tien suuntaisesti, suoraviivaisesti ja tasaisella nopeudella ja venymättömällä köydellä, hinattavan auton taka-akselin liikerata on traktrixin muotoinen.
4. Traktrix on epälineaarinen käydä, jonka suoraa pitkin vierivä a-säteinen ympyrä, jonka keskipiste on x-akselilla, leikkaa koko ajan kohtisuorasti.

Traktrixin asymptootti voi olla myös vaakasuora. Siinä tapauksessa käyrällä on pystysuora symmetria-akseli. Jos käyrä sijoitetaan koordinaatistoon siten, että sen asymptoottina on x-akseli ja symmetria-akselina y-akseli, sen kaarevuussäde sen kussakin pisteessä on $r=a\cot {\frac {x}{y}}$

Kun traktrix pyörähtää asymptoottinsa ympäri, pyörähdyspintana saadaan pseudopallo, joka on siitä erikoinen, että sen Gaussin kaarevuus on pinnan joka kohdassa yhtä suuri, kuitenkin pallon pinnasta poiketen negatiivinen. Eugenio Beltrami osoitti vuonna 1868, että pseudopallon geometria on lokaalisti yhtäläinen hyperbolisen tason kanssa. Sen vuoksi sillä on huomattava merkitys epäeuklidisessa geometriassa.

Ominaisuuksia

Ketjuviiva traktrixin evoluuttana.

Traktrix voidaan parametroida yhtälöillä $x=t-\tanh(t),y=1/{\cosh(t)}$.

Traktrixin geometrisesta määritelmästä seuraa, että sen jokaisesta tangentista jää yhtä pitkä osa, a, sivuamispisteen ja käyrän asymptoorin väliin.

Traktrixin pisteiden $x_{1}$ ja $x_{2}$ välisen osuuden kaaren pituus, kun nämä pisteet ovat samalla puolella käyrän kärkipistettä, on $a\ln {\frac {x_{1}}{x_{2}}}$ Traktrixin ja sen asymptootin välisen alueen pinta-ala on ${\pi a^{2}}{2}$, mikä voidaan osoittaa integroimalla tai Mamikonin lauseen avulla.

Pyörähdyspinta, joka syntyy traktrixin pyörähtäessä asymptoottinsa ympäri, on pseudopallo.

Traktrix on transkendenttinen käyrä, toisin sanoen sitä ei voida määritellä polynomiyhtälöllä.

Käytännön sovelluksia

Vuonna 1927 P. G. A. H. Voigt patentoi torvikaiuttimen, joka perustui siihen oletukseen, että torven läpi kulkeva aaltorintama on pallomainen ja sen säde on vakio. Tarkoituksena oli minimoida häiriö, joka aiheutuu ääniaaltojen heijastumisesta torven sisällä. Tämä saavutettiin parhaiten, kun torvi tehtiin traktrixin pyörähdyskappaleen muotoiseksi.

Poikkileikkaukseltaan traktrixin muotoisia puristimia käytetään yleisesti peltien [[taivutus (valmistusteknikka)|taivuttamiseen.

Mekaanisen tehonsiirron kannalta traktrix on erityisen edullinen muoto jakohihnan hampaille. Tämä muoto minimoi hampaisiin kohdistuvan kitkan, koska tällöin ne toisiinsa kiinittyessään ja jälleen irrotessaan liukuvat mahdollisimman vähän. Aikaisemmin jakohinnoissas käytettiin trapetsoidin tai ympyrän muotoisia hampaita, mikä aiheutti merkittävästi liukumista ja kitkaa.

Piirustusvälineitä

Loka-marraskuussa 1692 Christiaan Huygens suunnitteli laitteen, joiden avulla traktrix voitaisiin piirtää sen geometriseen määritelmään nojautuen siten, että vetävä laite etenee suoraviivaisesti tasaisella nopeudella. Myöhemmin samasta idesta esitettiin kehittyneempiä versiota, jolloin samalla laitteella olisi voitu suorittaa muitakin matemaattisia tehtäviä:

• Vuonna 1693 Gottfried Wilhelm Leibniz esitti "yleisen vetävän koneen" periaatteen. Teoriassa tällaisella koneella voitaisiin integroida mikä tahansa ensimmäisen asteen differentiaaliyhtälö. Kyseessä oli eräänlainen analogialaskin, mutta sellaisen rakentaminen Leibnizin ajan teknologialla oli epäkäytännöllistä eikä sitä koskaan toteutettu.
• Vuonna 1706 John Perks rakensi traktrixiin perustuvan laitteen, jonka avulla voitiin toteuttaa hyperbolisten funktioiden neliöinti.
• Vuonna 1729 Giovanni Poleni rakensi vetävän koneen, jolla voitiin piirtää logaritmifunktion kuvaaja.