Evoluutta


Evoluutta on käyrän kaarevuuskeskipisteiden muodostama ura. Yhtäpitävästi se voidaan määritellä käyrän normaalien verhokäyräksi. Alkuperäistä käyrää kutsutaan evolventiksi. Käyrän evoluutan määrääminen on eräs differentiaalilaskennan sovellus.[1]
Käyrän tai yleisemmin alimoniston evoluutta on sen normaalikuvauksen polttopisteiden joukko. Normaalikuvaus muodostetaan seuraavasti: Olkoon M sileä, säännöllinen alimonisto avaruudessa . Liitetään jokaiseen M:n pisteeseen p ja siitä alkavaan, pintaan M nähden kohtisuoraan vektoriin v piste p + v. Näin saatua Lagrangen kuvausta sanotaan normaalikuvaukseksi, ja sen polttopisteet muodostavat joukon M evoluutan.[2]
Jos käyrän evoluutta tunnetaan, itse käyrä voidaan piirtää asettamalla nuora evoluutalle ja kiinnittämällä se pisteeseen G. Pisteeseen A asetettu piirrin piirtää alkuperäisen käyrän, evolventin.
Historia[muokkaa | muokkaa wikitekstiä]
Kartioleikkausten evoluuttoja käsitteli jo Apollonius Pergeläinen (noin 250 eKr.) teoksensa Konika (Kartioleikkauksista) V kirjassa.[3]. Laajemmin evoluuttoja tutki 1600-luvulla Christiaan Huygens, ja toisinaan ansion evoluuttojen teorian perustamisesta katsotaankin kuuluvan hänelle.[1] Huygens kehitti evoluuttojen teorian selvittääkseen, onko olemassa tautokroninen käyrä, toisin sanoen käyrä, jonka minkä tahansa pisteelle asetulta kappaleelta kuluisi yhtä pitkä aika, ennen kuin ne ovat vierineet käyrän alimpaan kohtaan. Tällaiseksi osoittautui sykloidi[4], joka on siitä erikoinen, että myös sen evoluutta on muodoltaan sykloidi[5]. Tämä seikka auttoi häntä konstruioimaan heilurin, jonka heilahdusaika pysyy mahdollisimman tarkoin vakiona[4]. Evoluuttoja tutkimalla Huyghens johti myös monia tuloksia, jotka myöhemmin voitiin todistaa myös differentiaali- ja integraalilaskennan avulla.[6]<r
Parametrimuodossa esitetyn käyrän evoluutta[muokkaa | muokkaa wikitekstiä]
Jos käyrällä on parametriesitys (x, y) = (f(t), g(t)), sen kuhunkin pisteeseen liittyvän kaarevuuskeskipisteen koordinaatit ovat
missä R on käyrän kaarevuussäde,
ja on käyrän tangenttivektorin
ja x-akselin välinen kulma. Tällöin on ja . Tässä ja tarkoittavat funktioiden f ja g derivaattoja t:n suhteen: ja .
Yhdistämällä nämä saadaan käyrän evoluutalle parametriesitys:
Erityisesti jos käyrä on jonkin funktion kuvaaja, jolloin , ja , lauseke yksinkertaistuu muotoon
.[8]
Evoluutan ominaisuuksia[muokkaa | muokkaa wikitekstiä]

Seuraavassa käytetään säännölliselle käyrälle parametriesitystä , jolloin sen evoluutta voidaan esittää muodossa
Säännöllisen käyrän ominaisuuksia tutkittaessa on edullista käyttää parametrina sen kaaren pituutta , koska silloin ja . Silloin evoluutan tangenttivektoriksi saadaan
Tästä yhtälöstä seuraavat seuraavat evoluutan ominaisuudet:
- Pisteissä, joissa , evoluutta ei ole säännöllinen. Tämä merkitsee, että pisteitä, joissa käyrän kaarevuus saa lokaalin maksimi- tai minimiarvon, vastaa evoluutalla kärkipiste, kuten jäljempänä olevat kuvat paraabelin, ellipsin, sykloidin ja nefroidin evoluutoista osoittavat.
- Jos jokin evoluutan kaari ei sisällä tällaista kärkipistettä, kaaren pituus on yhä suuri kuin kaarevuussäteiden erotus sen päätepisteistä. Tämän seikan avulla voidaan helposti todistaa oskuloivia ympyröitä koskeva Taitin-Kneserin lause.[9]
- Käyrän normaalit pisteissä, jossa sillä on nollasta poikkeava kaarevuus, ovat sen evoluutan tangentteja. Sen sijaan käyrän normaalit pisteissä, joissa sen kaarevuus on nolla, ovat sen evoluutan asymptootteja. Näin ollen evoluutta on samalla käyrän normaalien verhokäyrä.
- Paralleelisilla käyrillä eli käyrillä, joiden välinen etäisyys on vakio, on sama evoluutta.
Todistus: Käyrällä, jonka etäisyys annetusta käyrästä on , on parametriesitys ja kaarevuussäde Niinä sen evoluutta on
Esimerkkejä[muokkaa | muokkaa wikitekstiä]
Paraabelin evoluutta[muokkaa | muokkaa wikitekstiä]
Paraabelille, jolla on parametriesitys , saadaan edellä esitettyjen kaavojen avulla evoluutan parametriesitykseksi:
Ellipsin evoluutta[muokkaa | muokkaa wikitekstiä]

Ellipsillä on parametriesitys Sen evoluutalle saadaan parametriesitys[11]
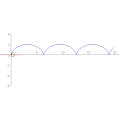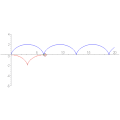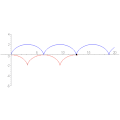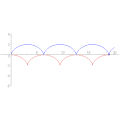
Sykloidin evoluutta[muokkaa | muokkaa wikitekstiä]

Sykloidilla on parametriesitys . Sen evoluutalle saadaan parametriesitys[12]
Joidenkin käyrien evoluuttoja[muokkaa | muokkaa wikitekstiä]

Kuten edellä todettiin, paraabelin evoluutta on puolikuutioinen paraabeli, ellipsin evoluutta astroidi ja sykloidin evoluutta sykloidi. Ympyrän evoluutta käsittää vain sen keskipisteen. Suoralla ei varsinaisesti ole evoluuttaa, mutta sen evoluutan voidaan sanoa olevan äärettömän kaukainen ideaalipiste.
Nefroidin evoluutta on toinen, alkuperäistä puolet pienempi nefroidi. Astroidin evoluutta on kaksi kertaa alkuperäisen kokoinen nefroidi. Kardioidin evoluutta on kardioidi, joka on kooltaan kolmasosa alkuperäisestä. Deltoidin evoluutta on kolme kertaa alkuperäisen kokoinen deltoidi. Logaritmisen spiraalin evoluutta on toinen logaritminen spiraali, joka eräissä tapauksissa yhtyy alkuperäisiin spiraaleihin. Traktrix-käyrän evoluutta on ketjuviiva.[13]
-
Ellipsin evoluutta on astroidi
-
Ellipsin evoluutta säteiden jatkeiden verhokäyränä
-
Astroidin evoluutta näyttää astroidilta
-
Sykloidin evoluutta
-
Episykloidin evoluutta
-
Tractrixin evoluutta on ketjukäyrä
Lähteet[muokkaa | muokkaa wikitekstiä]
- ↑ a b Jaakko Forsman, J. A. Wecksell, I. Havu, Hannes Salovaara: ”Evoluutta”, Pieni tietosanakirja, 1. osa (A - Isonzo), s. 851. Otava, 1925. Teoksen verkkoversio.
- ↑ V. I. Arnold, A. N. Varchenko, S. M. Zade: The Classification of Critical Poionts, Cautsics and Wave Fronts: Singularities of Differentiable Maps, Vol 1. Birkhäuser, 1985. ISBN 0-8176-3187-9.
- ↑ Apollonius of Perga History of Mathematics, Biographies. Viitattu 2.12.2023.
- ↑ a b Tautochrone Problem Wolfram MathWorld. Eric W. Weisstein. Viitattu 2.12.2023.
- ↑ Cycloid Wolfram MathWorld. Eric W. Weisstein. Viitattu 2.12.2023.
- ↑ Joella G. Yoder: Unrolling Time: Christiaan Huygens and the Mathematization of Nature. Cambridge University Press, 2004.
- ↑ Evolute ((Lähde koko osiolle tähän saakka)) Wolfram MathWorld. Eric W. Weisstein. Viitattu 2.12.2023.
- ↑ Frank Ayres Jr.; Elliott Mendelson: ”Curvature”, Schaum's outline of Theory and Problems of Differential and Integral Calculus (3rd Ed.), s. 149. McGraw-Hill, 1992. ISBN 0071125310.
- ↑ Osculating curves: around the Tait-Kneser theorem. The Mathematical Intelligencer, 2013, 35. vsk, nro 1, s. 61–66. doi:10.1007/s00283-012-9336-6.
- ↑ Samanlaisia sanoja: parabola ((lähde suomenkieliselle termille)) fi.opentran.net. Viitattu 2.12.2023.
- ↑ R. Courant: Vorlesungen über Differential- und Integralrechnung. Band 1, s. 268. Springer-Verlag, 1955.
- ↑ Cycloid Evolute Wolfram MathWorld. Eric W. Weisstein. Viitattu 2.12.2023. [vanhentunut linkki]
- ↑ Evolute Wolfram MathWorld. Eric W. Weisstein. Viitattu 2.12.2023.




















![{\displaystyle {\vec {x}}={\vec {c}}(t),\;t\in [t_{1},t_{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c39b96578c926c9cfc44b8bab1621e67aac866f9)