Logaritminen spiraali
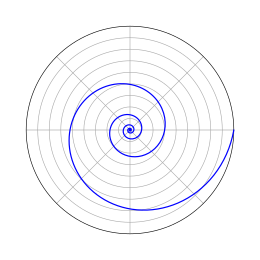






Logaritminen spiraali eli tasakulmainen spiraali[1] on itsesimilaarinen spiraalimainen käyrä, joka esiintyy usein luonnossa. Sen kuvasi ensimmäisenä Descartes, ja sen ominaisuuksia tutki myöhemmin tarkemmin Jakob Bernoulli, joka antoi sille nimen Spira mirabilis ’ihmeellinen spiraali’.
Käyrän yhtälö[muokkaa | muokkaa wikitekstiä]
Napakoordinaatistossa () logaritmisen spiraalin yhtälö on
tai
missä e on Neperin luku, ja a ja b ovat vakiona pysyviä positiivisia reaalilukuja.
Karteesisessa koordinaatistossa käyrä voidaan esittää parametrimuodossa:
missä ja ovat reaalisia vakioita.
Logaritmisella spiraalilla on se huomattava ominaisuus, että sen jokaisessa pisteessä käyrän tangentin muodostaa yhtä suuren kulman spiraalin keskuksesta eli navasta[1] alkavan puolisuoran kanssa. Tämän vakiokulman f ja käyrän yhtälössä esiintyvän vakion b välillä on yhteys:
- eli
Differentiaaligeometrian käsittein tämä yhteys voidaan ilmaista seuraavasti:
missä r ja ovat käyrän mielivaltaisen pisteen napakoordinaatit.
Lausekkeen derivaatta on verrannollinen parametriin . Toisin sanoen se ilmoittaa, kuinka "tiheästi" ja kumpaan suuntaan spiraali kiertyy. Rajatapauksessa, kun (), spiraalista tulee -säteinen ympyrä. Toisaalta kun :n annetaan kasvaa rajattomasti (f -> 0), spiraali lähestyy puolisuoraa. Kulman f komplementtikulmaa sanotaan spiraalin kaltevuuskulmaksilähde? (engl. pitch).
Spira mirabilis ja Jacob Bernoulli[muokkaa | muokkaa wikitekstiä]
Logaritmisesta spiraalista käytetään myös latinalaista nimeä Spira mirabilis, "ihmeellinen spiraali". Vaikka muut matemaatikot olivat tutkineet sitä jo aikaisemmin, tämän nimen käyrälle antoi Jacob Bernoulli,[1] koska häntä kiehtoivat sen ainutlaatuiset matemaattiset ominaisuudet: jokaisella kierroksella keskuksen ympäri spiraalin koko kasvaa, mutta sen muoto pysyy samana. Tätä ominaisuutta sanotaan itsesimilaarisuudeksi. Mahdollisesti juuri tämän ainutlaatuisen ominaisuutensa vuoksi spira mirabilis esiintyy monessa yhteydessä elollisessa luonnossa, esimerkiksi nautilus-helmiveneiden kuorissa ja auringonkukan mykerössä. Jacob Bernoulli ilmoitti toivomuksenaan, että hänen hautakiveensä kaiverrettaisiin logaritminen spiraali ja lause Eadem mutata resurgo ("Nousen jälleen muuttuneena ja silti ennallani"), mutta väärinkäsityksen vuoksi siihen kaiverrettiinkin Arkhimedeen spiraali.[1]
Ominaisuudet[muokkaa | muokkaa wikitekstiä]
Logaritminen spiraali eroaa Arkhimedeen spiraalista siinä, että käyrän ja sen keskuksesta lähtevän puolisuoran leikkauspisteiden väliset etäisyydet kasvavat keskuksesta etäännyttäessä geometrisen sarjan mukaan, kun taas Arkhimedeen spiraalissa tämä etäisyys on vakio. Jos sitä skaalataan origo skaalauskeskuksena tekijällä , missä b on kokonaisluku, se kuvautuu itselleen; jos skaalaustekijä on jokin muu, saadaan sama käyrä, joka saataisiin myös kiertämällä sitä origon ympäri jonkin kulman verran. Logaritminen spiraali on myös yhtenevä involuuttansa, evoluuttansa ja keskuksensa suhteen muodostetun pedaalikäyränsä kanssa.
Lähtemällä pisteestä ja etenemällä spiraalia pitkin sisäänpäin sen keskus voidaan kiertää rajattoman monta kertaa ilman, että sitä koskaan saavutaan. Kuitenkin tämän käyrän osan pituus on äärellinen, tai tarkemmin sanottuna sen pituuden raja-arvo, kun , on äärellinen. Tämän totesi ensimmäisenä Evangelista Torricelli jo ennen kuin differentiaali- ja integraalilaskenta keksittiin.[2] Tarkemmin sanottuna spiraalin tämän osan pituus on , missä on pisteen etäisyys origosta suoraa pitkin mitattuna.
Kompleksitasossa eksponenttifunktio kuvaa kaikki suorat, jotka eivät ole reaali- eivätkä imaginaariakselin suuntaisia, logaritmisille spiraaleille, joiden keskus on origossa. Kääntäen jokainen tällainen logaritminen spiraali saadaan jonkin suoran kuvaksi eksponenttifunktiolla. Kuvana saatavan spiraalin kaltevuuskulma on alkuperäisen suoran ja imaginaariakselin välinen kulma.
Funktio , missä on kompleksiluku, jonka imaginaariosa ei ole nolla, kuvaa kompleksitason realiakselin logaritmiselle spiraalille.
Kultainen spiraali on logaritminen spiraali, jonka pisteiden etäisyys kasvaa kultaisen leikkauksen suhteessa kierrettäessä origon ympäri 90 astetta. Sen kaltevuuskulma on noin 13,03239 astetta. Sitä voidaan approksimoida "Fibonaccin spiraalilla", joka muodostuu sarjasta ympyrän kehän neljänneksiä, joiden säteet ovat verrannollisia Fibonaccin lukujonon lukuihin.
Logaritminen spiraali luonnossa[muokkaa | muokkaa wikitekstiä]
Useissa luonnonilmiöissä esiintyy käyriä, jotka ovat ainakin likipitäen logaritmisen spiraalin muotoisia. Esimerkiksi muuttohaukka lähestyy saalistaan logaritmista spiraalia myöten. Se näkee tarkimmin suuntaan, joka muodostaa tietyn suuruisen kulman sen lentosuuntaan nähden; kun se pitää lentosuuntansa ja saaliin suunnan välisen kulman vakinaisesti tämän suuntaisena, lentoreitiksi muodostuu logaritminen spiraali, jonka kaltevuuskulma on kyseisen kulman suuruinen.[3][1]
Hyönteiset lähestyvät usein keinotekoisia valonlähdeitä logaritmisen spiraalin muotoista reittiä pitkin. Luonnossa ne suunnistautuvat siten, että lentosuunnan ja valonlähteen suunnan välinen kulma pysyy vakiona. Luonnossahan yleensä ainoa valon lähde on aurinko tai yöllä lentävien lajien tapauksessa kuu. Molemmat ovat niin kaukana, että hyönteisen lentäessä suoraan valonlähteen suunnan ja hyönteisen lentosuunnan välinen kulma pysyy käytännössä vakiona. Kun keinotekoiset valonlähteet kuitenkin ovat paljon lähempänä, ne voivat harhauttaa hyönteisen kiertämään niitä spiraalimaista reittiä myöten.[4]
Lähellä logaritmista spiraalia ovat muodoltaan myös:
- Kierteisgalaksien kierrehaarat.[5] Omalla galaksillamme, Linnunradan galaksilla, tällaisia kierrehaaroja on useita, ja niiden kaltevuuskulmat ovat noin 12 astetta.[6]
- Sarveiskalvon hermot[7]
- Trooppisiin hirmumyrskyihin liittyvät sadealueet[8]
- Monet biologiset rakenteet, kuten nilviäisten kuoret.[9] Syynä lienee, että ne rakentuvat yhdenmuotoisten osien laajetessa samaan tapaan kuin monikulmiot oheisessa kuviossa.
- Rantaviiva hiekkarannoilla saattaa meren aaltojen heijastumisen ja diffraktion vaikutuksesta vähitellen muotoutua suunnilleen logaritmisen spiraalin kaaren muotoiseksi. Niin on tapahtunut esimerkiksi Half Moon Bayn rannalla Kaliforniassa.[10]
Katso myös[muokkaa | muokkaa wikitekstiä]
Lähteet[muokkaa | muokkaa wikitekstiä]
- Logarithmic Spiral Wolfram MathWorld. Viitattu 4.3.2015.
- Equiangular Spiral (or Logarithmic Spiral) and Its Related Curves jwilson.coe.uga.edu. 1999. Arkistoitu 1.5.2021. Viitattu 4.3.2015.
- Spira Mirabilis - Wonderful Spiral cut-the-knot.org. Viitattu 4.3.2015.
Viitteet[muokkaa | muokkaa wikitekstiä]
- ↑ a b c d e Alex Bellos: ”8. luku, Kultasormi”, Kiehtova matematiikka, Seikkailu numeroiden ihmemaassa, s. 293-295. Suomentanut Eero Sarkkinen. Bookwell Oy, 2011. ISBN 978-951-0-37676-8.
- ↑ Carl Benjamin Boyer: The history of the calculus and its conceptual development, s. 133. Courier Dover Publications, 1949. ISBN 978-0-486-60509-8. Teoksen verkkoversio.
- ↑ Organismal Biology: Flying Along a Logarithmic Spiral. Science, 2000, nro 290. Artikkelin verkkoversio.
- ↑ John Himmelman: Discovering Moths: Nighttime Jewels in Your Own Backyard, s. 63. Down East Enterprise Inc. 978-0-89272-528-1. Teoksen verkkoversio. [vanhentunut linkki]
- ↑ G. Bertin, C. C. Lin: Spiral structure in galaxies: a density wave theory, s. 78. MIT Press, 1996. 978-0-262-02396-2. Teoksen verkkoversio.
- ↑ David J. Darling: The universal book of mathematics: from Abracadabra to Zeno's paradoxes, s. 188. John Wiley & Sons, 2004. ISBN 978-0-471-27047-8. Teoksen verkkoversio.
- ↑ Transgenic corneal neurofluorescence in mice: a new model for in vivo investigation of nerve structure and regeneration. Invest Ophthalmol Vis Sci., huhtikuu 2007, nro 48(4), s. 1535-42.
- ↑ Andrew Gray: Treatise on physics, vol. 1, s. 356–357. Churchill, 2901. Teoksen verkkoversio.
- ↑ Michael Cortie, István Hargittai, Clifford A. Pickover: The form, function, and synthesis of the molluscan shell, s. 370. World Scientific, 1992. Teoksen verkkoversio.
- ↑ Anton Micallef: Beach management: principles and practice, s. 14. Earthscan, 2009. ISBN 978-1-84407-435-8. Teoksen verkkoversio.
Aiheesta muualla[muokkaa | muokkaa wikitekstiä]
- Spira mirabilis (historiaa ja matematiikkaa) jwilson.coe.uga.edu. Arkistoitu 15.7.2007. Viitattu 4.3.2015.
- Astronomy Picture of the Day (hurrikaani Isabel vs. Pyörregalaksipool Galaxy) apod.nasa.gov. 23.9.2005.
- Astronomy Picture of the Day (taifuuni Rammasun (2008)) apod.nasa.gov.
- SpiralZoom.com (Opetustarkoituksiin laadittu sivusto spiraaleista luonnossa ja myyttisessä mielikuvituksessa) SpiralZoom.com.
- Spira Mirabilis (JSXGraphin avulla tehty JavaSript-ohjelma, jolla voidaan piirtää logaritminen spiraali) jsxgraph.uni-bayreuth.de.























