Särmä (geometria)
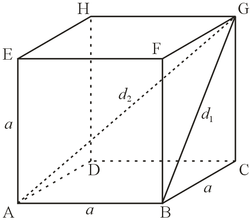



Särmä on geometriassa ja avaruusgeometriassa tietynlainen jana, jossa avaruuskappaleen tahkot kohtaavat. Särmä on myös jana, jonka molemmissa päissä on monitahokkaan kärjet.
Määritelmä[muokkaa | muokkaa wikitekstiä]
Kolmiulotteinen särmä[muokkaa | muokkaa wikitekstiä]
Suomen kielessä sanaa särmä käytetään vain avaruuskappaleissa, joiden tahkot ovat tasoja ja tasojen leikkauskuviot eli särmät janoja. Avaruuskappaleissa vain sellaisia kärkiä yhdistäviä janoja kutsutaan särmiksi, jotka syntyvät kahden tahkon suuntaisen tason leikkauksista. Muut kärkien väliset janat ovat joko tahkon lävistäjiä tai kärkien välisiä avaruuslävistäjiä. Yksinkertaistaen voidaan sanoa, että särmät näkyvät ulospäin kappaleen pinnalla.
Yksiulotteinen särmä[muokkaa | muokkaa wikitekstiä]
Yksiulotteinen särmä syntyy, kun kaksi pistettä yhdistetään janalla.
Kaksiulotteinen särmä[muokkaa | muokkaa wikitekstiä]
Kaksiulotteinen monikulmio syntyy tasossa siten, kun useammasta janasta muodostuva murtoviiva on suljettu. Jokaisessa kulmassa on kärki, joita yhdistävät janat ovat monikulmion sivuja. Kaksiulotteiset sivut vastaavat tasokuvioissa avaruuskappaleiden särmiä. Muut monikulmion kärkiä yhdistävät janat ovat sen lävistäjiä.
Neliulotteinen särmä[muokkaa | muokkaa wikitekstiä]
Neliulotteisessa avaruudessa särmät syntyvät, kun 3 tai useampi taso leikkaa toisensa.
Katso myös[muokkaa | muokkaa wikitekstiä]
Lähteet[muokkaa | muokkaa wikitekstiä]
- Väisälä, Kalle: Geometria. Porvoo: Wsoy, 1959. Teoksen verkkoversio (pdf).
- Weisstein, Eric W.: Polygon Edge (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)
- Weisstein, Eric W.: Polyhedron Edge (Math World – A Wolfram Web Resource) Wolfram Research. (englanniksi)