Paraboloidi

Pyörähdysparaboloidi

Hyperbolinen paraboloidi

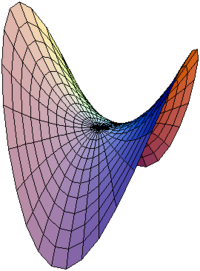
Paraboloidi on kolmiulotteinen kappale matemaattisessa avaruudessa. Paraboloideja on kahta tyyppiä, elliptinen paraboloidi ja hyperbolinen paraboloidi. Elliptistä paraboloidia kuvaa yhtälö:

$\left( \frac{x}{a} \right) ^2 + \left( \frac{y}{b} \right) ^2 + 2z = 0$.

Hyperbolista paraboloidia kuvaa yhtälö:

$\left( \frac{x}{a} \right) ^2 - \left( \frac{y}{b} \right) ^2 + 2z = 0$

Elliptinen paraboloidi on muodoltaan kuppimainen. Jos elliptisen paraboloidin yhtälössä a = b, kappale on ympyräpohjainen ja sitä kutsutaan pyörähdysparaboloidiksi. Tällainen kappale syntyy, kun paraabeli pyörähtää akselinsa ympäri. Pyörähdysparaboloidia voidaan käyttää peilinä, koska siinä ei esiinny pallopeileille ominaista pallopoikkeamaa.

Hyperbolista paraboloidia kutsutaan joskus satulapinnaksi sen muodon takia.