EM-algoritmi

EM-algoritmi (EM on lyhenne sanoista Expectation-Maximization eli odotusarvon maksimointi) on tilastotieteessä käytetty iteratiivinen menetelmä suurimman uskottavuuden estimaattien löytämiseksi tilastollisten mallien parametreille tilanteessa, jossa osa tiedosta puuttuu. Puuttuva tieto voi olla esimerkiksi piilevä luokkamuuttuja, josta ei saatu lainkaan havaintoja.

Vanhan uskollisen purkautumisiin liittyvän aineiston EM-klusterointi. Jokin aloitusmalli sovitetaan havaittuun aineistoon. (Akseleiden erilaisten mitta-asteikoiden vuoksi jakauma näyttää kahdelta hyvin litteältä ja leveältä soikiolta.) Ensimmäiset iteraatiot muuttavat mallia huomattavasti, minkä jälkeen malli konvergoi kohti geysirin purkausten tyypillisimpiä arvoyhdistelmiä. Visualisointi tehty ELKI:llä.

Kuvaus

Olkoon $\theta ={\big (}\theta _{1},\theta _{2},...,\theta _{k}{\big )}$ aineiston $Y$ jakaumaan liittyvien tuntemattomien parametrien muodostama vektori. Täydelliselle aineistolle uskottavuusfunktio voidaan kirjoittaa muodossa

$L(Y|\theta )=\prod _{i=1}^{n}f(y_{i},\theta )$ .

Hyvin usein osa oleellisista tiedosta jää kuitenkin havaitsematta. Täydellinen data voidaan jakaa kahteen osaan: havaittuun aineistoon $X$ ja puuttuvaan aineistoon $Z$. Tällöin täydellisen aineiston uskottavuus saadaan kirjoitettua muotoon

$L(X,Z|\theta )=L(X|\theta )L(Z|X,\theta )$.

Ottamalla logaritmi puolittain lauseke saadaan muotoon

$\log L(X|\theta )=\log L(X,Z|\theta )-\log L(Z|X,\theta )$.

Oletetaan mallin parametreille tunnettu arvo $\theta =\theta ^{(t)}$ iteraatiolla $t$. Tällöin edellä esitetyn lausekkeen odotusarvo puuttuvien havaintojen suhteen on

$\operatorname {E} _{Z|X,\theta =\theta ^{(t)}}\left[\log L(X|\theta )\right]=\operatorname {E} _{Z|X,\theta =\theta ^{(t)}}\left[\log L(X,Z|\theta )-\log L(Z|X,\theta )\right]$.

Merkitään nyt täydellisen aineiston logaritmista uskottavuutta seuraavasti:

${\begin{aligned}Q(\theta |\theta ^{(t)})&=\operatorname {E} _{Z|X,\theta =\theta ^{(t)}}\left[\log L(X,Z|\theta )\right]\\&=\int \log L(X,Z|\theta )L(Z|X,\theta ^{(t)})\,dZ\end{aligned}}$

Algoritmissa toistetaan vuorotellen kahta askelta:

E-askel: Johda termin $Q(\theta |\theta ^{(t)})$ lauseke.

M-askel: Etsi parametrille ${\boldsymbol {\theta }}$ sellainen arvo ${\boldsymbol {\theta }}^{(t+1)}$, että uskottavuus maksimoituu.

Aluksi tuntemattomille parametreille asetetaan alkuarvot $\theta ^{(0)}$. Ensimmäinen iteraatio aloitetaan siis laskemalla $Q(\theta |\theta ^{(0)})$.

Varsinainen iteratiivinen algoritmi joudutaan johtamaan erikseen kullekin tilanteelle.

Ominaisuuksia

Käytettäessä EM-algoritmia uskottavuusfunktion arvo kasvaa jokaisella iteraatiolla ja parametrin estimaatti lähestyy monotonisesti suurimman uskottavuuden estimaattia.

EM-algoritmi on hyödyllinen uskottavuuden tullessa eksponenttisesta perheestä: E-askel sievenee tyhjentävien tunnuslukujen odotusarvojen summaksi ja M-askeleessa maksimoidaan lineaarista funktiota. Tällaisessa tapauksessa voidaan usein johtaa suljettu muoto askelten päivittämiseksi Sundbergin kaavalla (Rolf Sundberg julkaisi kaavan, mutta hän hyödynsi Per Martin-Löfin ja Anders Martin-Löfin julkaisemattomia tuloksia).

Esimerkkejä

Gaussinen sekoitus

Animaatio, joka havainnollistaa kaksikomponenttisen sekoitusjakauman sovittamista EM-algoritmilla Old Faithful aineistoon. Algoritmin askeleet satunnaisesta aloituksesta konvergenssiin.

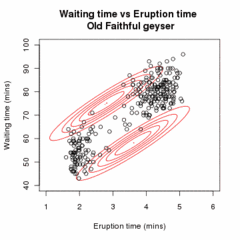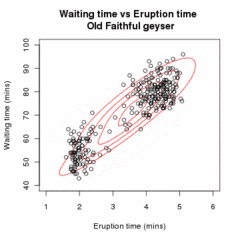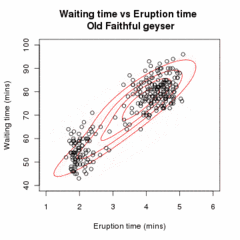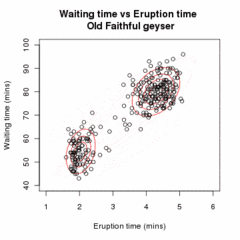
Olkoon $\mathbf {x} =(\mathbf {x} _{1},\mathbf {x} _{2},\ldots ,\mathbf {x} _{n})$ $n$-kokoinen otos riippumattomia havaintoja kahdesta moniulotteisesta normaalijakaumasta, ulottuvuuksien määrä $d>1$. Olkoot $\mathbf {z} =(z_{1},z_{2},\ldots ,z_{n})$ latentteja muuttujia, jotka kertovat kummasta ryhmästä kyseinen havainto on peräisin.

$X_{i}|(Z_{i}=1)\sim {\mathcal {N}}_{d}({\boldsymbol {\mu }}_{1},\Sigma _{1})$ \, ja \, $X_{i}|(Z_{i}=2)\sim {\mathcal {N}}_{d}({\boldsymbol {\mu }}_{2},\Sigma _{2})$,

missä

$\operatorname {P} (Z_{i}=1)=\tau _{1}\,$ ja $\operatorname {P} (Z_{i}=2)=\tau _{2}=1-\tau _{1}$.

Tavoite on estimoida jakaumien tuntemattomat keskiarvot ja kovarianssit, sekä jakaumien sekoittumista kuvaava arvo $\tau$:

$\theta ={\big (}{\boldsymbol {\tau }},{\boldsymbol {\mu }}_{1},{\boldsymbol {\mu }}_{2},\Sigma _{1},\Sigma _{2}{\big )}$,

missä uskottavuusfunktio on:

$L(\theta ;\mathbf {x} ,\mathbf {z} )=P(\mathbf {x} ,\mathbf {z} \vert \theta )=\prod _{i=1}^{n}\sum _{j=1}^{2}\mathbb {I} (z_{i}=j)\ \tau _{j}\ f(\mathbf {x} _{i};{\boldsymbol {\mu }}_{j},\Sigma _{j})$,

missä $\mathbb {I}$ on indikaattorifunktio ja $f$ on moniulotteisen normaalijakauman tiheysfunktio. Tämä voidaan kirjoittaa uudelleen eksponenttisen perheen muotoon:

$L(\theta ;\mathbf {x} ,\mathbf {z} )=\exp \left\{\sum _{i=1}^{n}\sum _{j=1}^{2}\mathbb {I} (z_{i}=j){\big [}\log \tau _{j}-{\tfrac {1}{2}}\log |\Sigma _{j}|-{\tfrac {1}{2}}(\mathbf {x} _{i}-{\boldsymbol {\mu }}_{j})^{\top }\Sigma _{j}^{-1}(\mathbf {x} _{i}-{\boldsymbol {\mu }}_{j})-{\tfrac {d}{2}}\log(2\pi ){\big ]}\right\}.$

Voidaan huomata, että kullekin i indikaattori $\mathbb {I} (z_{i}=j)$ saa arvon yksi vain yhdellä j, ja toisella j indikaattorin arvo on nolla. Sisempi summa siis supistuu yhdeksi lausekkeeksi eikä summausta tarvita.

E-askel

Oletetaan, että meillä on parametrien estimaatit θ^(t). Tällöin Z_i:n ehdollinen jakauma voidaan kirjoittaa todennäköisyytenä Bayesin kaavan mukaisesti:

$T_{j,i}^{(t)}:=\operatorname {P} (Z_{i}=j|X_{i}=\mathbf {x} _{i};\theta ^{(t)})={\frac {\tau _{j}^{(t)}\ f(\mathbf {x} _{i};{\boldsymbol {\mu }}_{j}^{(t)},\Sigma _{j}^{(t)})}{\tau _{1}^{(t)}\ f(\mathbf {x} _{i};{\boldsymbol {\mu }}_{1}^{(t)},\Sigma _{1}^{(t)})+\tau _{2}^{(t)}\ f(\mathbf {x} _{i};{\boldsymbol {\mu }}_{2}^{(t)},\Sigma _{2}^{(t)})}}$.

Siten E-askel johtaa seuraavaan funktioon:

${\begin{aligned}Q(\theta |\theta ^{(t)})&=\operatorname {E} [\log L(\theta ;\mathbf {x} ,\mathbf {z} )]\\&=\operatorname {E} [\log \prod _{i=1}^{n}L(\theta ;\mathbf {x} _{i},\mathbf {z} _{i})]\\&=\operatorname {E} [\sum _{i=1}^{n}\log L(\theta ;\mathbf {x} _{i},\mathbf {z} _{i})]\\&=\sum _{i=1}^{n}\operatorname {E} [\log L(\theta ;\mathbf {x} _{i},\mathbf {z} _{i})]\\&=\sum _{i=1}^{n}\sum _{j=1}^{2}T_{j,i}^{(t)}{\big [}\log \tau _{j}-{\tfrac {1}{2}}\log |\Sigma _{j}|-{\tfrac {1}{2}}(\mathbf {x} _{i}-{\boldsymbol {\mu }}_{j})^{\top }\Sigma _{j}^{-1}(\mathbf {x} _{i}-{\boldsymbol {\mu }}_{j})-{\tfrac {d}{2}}\log(2\pi ){\big ]}\end{aligned}}$

M-askel

Huomataan, että $\tau ,(\mu _{1},\Sigma _{1})$ ja $(\mu _{2},\Sigma _{2})$ voidaan kukin maksimoida toisistaan riippumatta, sillä ne ovat edellä esitetyssä lausekkeessa eri termeissä.

Tarkastellaan aluksi parametria τ, jolla on rajoite τ₁ + τ₂=1:

${\begin{aligned}{\boldsymbol {\tau }}^{(t+1)}&={\underset {\boldsymbol {\tau }}{\operatorname {arg\,max} }}\ Q(\theta |\theta ^{(t)})\\&={\underset {\boldsymbol {\tau }}{\operatorname {arg\,max} }}\ \left\{\left[\sum _{i=1}^{n}T_{1,i}^{(t)}\right]\log \tau _{1}+\left[\sum _{i=1}^{n}T_{2,i}^{(t)}\right]\log \tau _{2}\right\}\end{aligned}}$

Tämä on samaa muotoa kuin binomijakauman suurimman uskottavuuden estimaatti. Siten

$\tau _{j}^{(t+1)}={\frac {\sum _{i=1}^{n}T_{j,i}^{(t)}}{\sum _{i=1}^{n}(T_{1,i}^{(t)}+T_{2,i}^{(t)})}}={\frac {1}{n}}\sum _{i=1}^{n}T_{j,i}^{(t)}$.

Tarkastellaan seuraavaksi parametrien $(\mu _{1},\Sigma _{1})$ estimaatteja:

${\begin{aligned}({\boldsymbol {\mu }}_{1}^{(t+1)},\Sigma _{1}^{(t+1)})&={\underset {{\boldsymbol {\mu }}_{1},\Sigma _{1}}{\operatorname {arg\,max} }}\ Q(\theta |\theta ^{(t)})\\&={\underset {{\boldsymbol {\mu }}_{1},\Sigma _{1}}{\operatorname {arg\,max} }}\ \sum _{i=1}^{n}T_{1,i}^{(t)}\left\{-{\tfrac {1}{2}}\log |\Sigma _{1}|-{\tfrac {1}{2}}(\mathbf {x} _{i}-{\boldsymbol {\mu }}_{1})^{\top }\Sigma _{1}^{-1}(\mathbf {x} _{i}-{\boldsymbol {\mu }}_{1})\right\}\end{aligned}}$

Tämä on samaa muotoa normaalijakauman painotetun SU-estimaatin kanssa, joten

${\boldsymbol {\mu }}_{1}^{(t+1)}={\frac {\sum _{i=1}^{n}T_{1,i}^{(t)}\mathbf {x} _{i}}{\sum _{i=1}^{n}T_{1,i}^{(t)}}}$ ja $\Sigma _{1}^{(t+1)}={\frac {\sum _{i=1}^{n}T_{1,i}^{(t)}(\mathbf {x} _{i}-{\boldsymbol {\mu }}_{1}^{(t+1)})(\mathbf {x} _{i}-{\boldsymbol {\mu }}_{1}^{(t+1)})^{\top }}{\sum _{i=1}^{n}T_{1,i}^{(t)}}}$.

Vastaavasti

${\boldsymbol {\mu }}_{2}^{(t+1)}={\frac {\sum _{i=1}^{n}T_{2,i}^{(t)}\mathbf {x} _{i}}{\sum _{i=1}^{n}T_{2,i}^{(t)}}}$ ja $\Sigma _{2}^{(t+1)}={\frac {\sum _{i=1}^{n}T_{2,i}^{(t)}(\mathbf {x} _{i}-{\boldsymbol {\mu }}_{2}^{(t+1)})(\mathbf {x} _{i}-{\boldsymbol {\mu }}_{2}^{(t+1)})^{\top }}{\sum _{i=1}^{n}T_{2,i}^{(t)}}}$.

Lopettaminen

Lopeta iterointi, jos $\log L(\theta ^{t};\mathbf {x} ,\mathbf {z} )$ ja $\log L(\theta ^{(t-1)};\mathbf {x} ,\mathbf {z} )$ ovat riittävän lähellä toisiaan (erotus alle jonkin ennalta asetetun kynnysarvon).

Yleistäminen

Yllä esitetty algoritmi voidaan yleistää useampien kuin kahden monimuuttujaisen normaalijakauman sekoituksille.

Historiaa

EM-algoritmin historia jaetaan usein kirjoittajien Dempster, Laird ja Rubin vuonna 1977 ilmestynyttä artikkelia edeltävään ja sitä seuraavaan aikaan. Kyseisessä artikkelissa annettiin runsaasti esimerkkejä algoritmin sovelluksista, ja kuvailtiin sen konvergenssiä ja muita perusominaisuuksia. Tätä artikkelia kutsutaan usein DLR-artikkeliksi.

Ennen DLR-artikkelia

Kirjallisuudessa ensimmäinen maininta liittyen EM-tyyppiseen algoritmiin esiintyy Newcombin vuoden 1886 artikkelissa kahden yksiulotteisen normaalijakauman sekoituksesta.

Vuonna 1960 Buck esitteli p-ulotteisen populaation keskiarvovektorin ja kovarianssimatriisin estimointia tilanteessa, jossa osa aineistosta puuttui. Hän käytti regressiota ja puuttuvien havaintojen selittämistä havaitulla aineistolla. Hänen menetelmässään tarvitut regressiokertoimet ja kovarianssimatriisin kerrointen korjaukset saadaan yhdellä täydellisten havaintojen informaatiomatriisin kääntämisellä ja sopivilla matriisilaskuilla. EM-algoritmin peruselementit esiintyvät Buckin menetelmässä.

EM-algoritmin soveltamista Markov-malleille käsiteltiin sarjassa artikkeleita: Baum ja Petrie (1966), Baum ja Eagon (1967) ja Baum, Petrie, Soules ja Weiss (1970). Nämä artikkelit sisältävät helposti yleistettävissä olevia konvergenssituloksia. Näissä artikkeleissa kehitetty algoritmi toimii myös perustana nykyään käytetyille piilo-Markov-mallien EM-algoritmeille.

Vuonna 1972 Orchard ja Woodbury esittelivät täydellisen ja ei-täydellisen aineiston logaritmisten uskottavuusfunktioiden välisen suhteen.

DLR-artikkelin jälkeen

Rajapyykkinä toimivan artikkelin jälkeen EM-algoritmia on sovellettu muun muassa neuroverkkoihin, koneoppimisessa, psykometriikassa ja lääketieteellisessä kuvantamisessa (esimerkiksi PET-kuvauksissa).