Tiheysfunktionaaliteoria

Tiheysfunktionaaliteoria (density functional theory, DFT) on laskennallisessa fysiikassa ja kemiassa käytetty kvanttimekaaninen menetelmä mikroskooppisten systeemien elektronirakenteen tutkimiseen. Menetelmää käytetään erityisesti kiinteän olomuodon fysiikassa sekä kvanttikemiassa. Perustan teorialle loivat Pierre Hohenberg ja Walter Kohn vuonna 1964 osoittaessaan, että elektronisysteemin perustilan elektronitiheys määrittää systeemin tilan yksiselitteisesti. Tällöin systeemin sisäenergia on mahdollista kirjoittaa aaltofunktion sijasta elektronitiheysfunktion funktionaalina, jolloin laskennalliset kustannukset kutistuvat merkittävästi. Kiinteän olomuodon fysiikassa tiheysfunktionaaliteoria on aina ollut suositumpi kuin aaltofunktiopohjaiset menetelmät ja kiinteän olomuodon tutkimisessa tiheysfunktionaaliteoriaa on käytetty jo 1970-luvulta asti. Kvanttikemistien suosioon menetelmä kuitenkin nousi vasta 1980-luvun lopulla uusien, kehittyneempien funktionaalien myötä. Vuonna 1998 kemian Nobelin palkinto myönnettiin Kohnille teorian keksimisestä ja John Poplelle laskennallisten menetelmien kehittämisestä.

Tiheysfunktionaaliteoria on teoriassa eksakti, mutta käytännössä kokonaisenergialausekkeessa esiintyvän vaihto- ja korrelaatiofunktionaalin oikeaa muotoa ei tunneta, joten funktionaalia joudutaan approksimoimaan. Tämän seurauksena myös tulokset ovat riippuvaisia käytetystä approksimaatiosta. Approksimaatiosta seuraavia puutteita tiheysfunktionaaliteoriassa ovat muun muassa:

• Yksikään approksimatiivinen funktionaali ei sisällä heikkoa dispersiovuorovaikutusta, mikä on ongelma esimerkiksi hiilivetyjä mallinnettaessa. Dispersiota voidaan approksimoida esimerkiksi empiirisillä korjauksilla. Dispersion arvioimista suoraan elektronitiheydestä käsin on myös esitetty .
• Perinteinen tiheysfunktionaaliteoria ei sisällä virittyneitä tiloja, koska virittyneen tilan elektronitiheys ei yksiselitteisesti määrää potentiaalia. Virittyneitä tiloja on kuitenkin mahdollista käsitellä ajasta riippuvan tiheysfunktionaaliteorian (time-dependent density functional theory, TD-DFT) avulla.
• Tiheysfunktionaaliteoria on tunnetusti surkea HOMO–LUMO-välin eli ylimmän miehitetyn ja alimman miehittämättömän orbitaalin energiaeron arvioimisessa.

Hohenberg–Kohn-teoreemat

Hohenberg–Kohn-teoreemat antavat teoreettisen oikeutuksen menetelmän käytölle. Ensimmäinen teoreema osoittaa, että systeemin perustilan elektronitiheys yksiselitteisesti määrää systeemin tilan. Toinen teoreema luo pohjan perustilan elektronitiheyden löytämiselle: oikeaa perustilan elektronitiheyttä voidaan lähestyä minimoimalla perustilan energiaa. Toisin sanoen oikea elektronitiheys antaa alimman mahdollisen perustilan energian. Tiheysfunktionaaliteoria on laskennallisesti huomattavasti kevyempi kuin monet korreloituneet Hartree–Fock-johdannaiset, kun N:n elektronin systeemin 3N-ulotteisen aaltofunktion sijasta ratkaistaan vain 3-ulotteista elektronitiheyttä.

Monielektronisysteemeissä ydinten ja elektronien liike yleensä erotetaan toisistaan (Born–Oppenheimer eli adiabaattinen approksimaatio), jolloin elektronit liikkuvat ydinten muodostamassa "staattisessa" potentiaalissa. Stationääritilaa $\Psi ({\vec {r}}_{1},...,{\vec {r}}_{N})=\Psi$ voidaan kuvata ajasta riippumattoman Schrödingerin yhtälön avulla:

${\hat {H}}\Psi =({\hat {T}}+{\hat {V}}_{ee}+{\hat {V}}_{ext})\Psi =\left(-\sum _{i}^{N}{\frac {1}{2}}\nabla ^{2}+\sum _{i}^{N}\sum _{j>i}{\frac {1}{|{\vec {r}}_{i}-{\vec {r}}_{j}|}}-\sum _{i}^{N}\sum _{k}{\frac {Z_{k}}{|{\vec {r}}_{i}-{\vec {R}}_{k}|}}\right)\Psi =E\Psi$

Yllä ${\hat {H}}$ on systeemiä kuvaava Hamiltonin operaattori ja $E$ systeemin kokonaisenergia. ${\vec {R}}_{k}$ on atomiytimen k paikkavektori ja $Z_{k}$ ytimen varaus. ${\hat {T}}$ on elektronien kineettinen energia, ${\hat {V}}_{ee}$ elektronien välinen coulombinen vuorovaikutus ja ${\hat {V}}_{ext}$ elektronien ja atomiydinten vuorovaikutus eli atomien virittämä ulkoinen potentiaali. Kineettisen energian ${\hat {T}}$ ja elektronirepulsion ${\hat {V}}_{ee}$ operaattorit ovat samoja kaikissa N-elektronisysteemeissä, mutta ulkoinen potentiaali, jossa elektronit sijaitsevat vaihtuu systeemistä toiseen. Yllä on käytetty niin kutsuttuja atomiyksiköitä, jolloin vakioita ei tarvitse pyörittää erikseen mukana. Atomiyksiköissä energian yksikkö on Hartree, E_h = 27,21138386 eV = 4,35974394·10⁻¹⁸ J.

Ensimmäisen Hohenberg–Kohn teoreeman todistus on suoraviivainen reductio ad absurdum: oletetaan, että kahden toisistaan eroavan ulkoisen potentiaalin, ${\hat {V}}_{ext}$ ja ${\hat {V}}_{ext}'$, perustilan elektronitiheys $\rho ({\vec {r}})=|\Psi ({\vec {r}})|^{2}=|\Psi '({\vec {r}})|^{2}$ olisi sama. Jos potentiaalit poikkeavat toisistaan enemmän kuin pelkän vakion verran, myös potentiaaleja vastaavat eri aaltofunktiot, $\Psi$ ja $\Psi '$. Variaatioperiaatteen mukaan oikea aaltofunktio antaa alhaisimman perustilan energian. Jos siis operoidaan aaltofunktiota $\Psi '$ toisen systeemin Hamiltonin operaattorilla ${\hat {H}}$ saadaan perustilan energia, joka on oikeaa perustilan arvoa suurempi:

$E_{0}<\left\langle \Psi '|{\hat {H}}|\Psi '\right\rangle =\left\langle \Psi '|{\hat {H}}'|\Psi '\right\rangle +\left\langle \Psi '|{\hat {H}}-{\hat {H}}'|\Psi '\right\rangle =E_{0}'+\left\langle \Psi '|({\hat {T}}+{\hat {V}}_{ee}+{\hat {V}}_{ext})-({\hat {T}}+{\hat {V}}_{ee}+{\hat {V}}_{ext}')|\Psi '\right\rangle$

$\Rightarrow E_{0}<E_{0}'+\int \rho ({\vec {r}})\left({\hat {V}}_{ext}-{\hat {V}}_{ext}'\right)d{\vec {r}}$

Jos kuitenkin aaltofunktiota $\Psi$ operoidaan toisella Hamiltonin operaattorilla ${\hat {H}}'$ saadaan tulokseksi

$E_{0}'<E_{0}-\int \rho ({\vec {r}})\left({\hat {V}}_{ext}-{\hat {V}}_{ext}'\right)d{\vec {r}}$

Yhdistämällä kaksi edellistä yhtälöä, saadaan tulokseksi $E_{0}+E_{0}'<E_{0}'+E_{0}\Leftrightarrow 0<0$ mikä on ristiriita, joten alun oletus on virheellinen: perustila riippuu yksiselitteisesti elektronitiheydestä.0

Kohn–Sham-menetelmä

Vaikka Hohenbergin ja Kohnin teoreemat osoittavat, että elektronitiheys on perustilaan liittyvä yksiselitteinen suure, eivät teoreemat kuitenkaan auta elektronitiheyden löytämisessä. Käytännön menetelmän perustilan löytymiseksi esittivät Kohn ja Sham vuonna 1965 . Kohnin ja Shamin menetelmässä perustilan energia ratkaistaan kahden rinnakkaisen systeemin avulla, joista toinen laskee systeemin kokonaisenergian elektronitiheyden avulla samalla kun toinen määrittää elektronien kineettisen energian Kohn–Sham-orbitaalien avulla. Jälkimmäinen systeemi koostuu Hartree–Fock-menetelmän kaltaisista ei-vuorovaikuttavista yksielektroniorbitaaleista, jotka sijaitsevat ulkoisessa potentiaalissa. Orbitaalien avulla kineettisen energian osuus on mahdollista laskea melko tarkasti.

Hohenberg–Kohnin teoreemojen perusteella on perustilan energia elektronitiheyden funktionaali:

$E_{0}[\rho _{0}]=T[\rho _{0}]+E_{ee}[\rho _{0}]+E_{ext}[\rho _{0}]$

Yllä $T[\rho ]$ on elektronien kineettinen energia, $E_{ee}[\rho ]$ on elektronien välisen vuorovaikutuksen potentiaalienergia ja $E_{ext}[\rho ]$ ulkoiseen potentiaaliin liittyvä energia, $E_{ext}[\rho ]=\int \rho ({\vec {r}})V_{ext}d{\vec {r}}$. Kineettisen energian ja elektroni–elektroni-termin energia on sama kuin kineettisen ja elektroni–elektroni-operaattorin odotusarvo:

$\left\langle \Psi |{\hat {T}}+{\hat {V}}_{ee}|\Psi \right\rangle =T[\rho ]+E_{ee}[\rho ]=F_{HK}[\rho ]$

missä $F_{HK}[\rho ]$ on niin kutsuttu Hohenberg–Kohn funktionaali. Koska kineettinen energia eikä elektronien välinen repulsio ovat systeemistä riippumattomia funktionaaleja, on Hohenberg–Kohn funktionaali riippumaton systeemistä. Vaikka tiheysfunktionaaliteoria on itsessään eksakti teoria, on ongelmana juuri Hohenberg–Kohn funktionaali, jolle ei ole olemassa lauseketta vaan funktionaalia joudutaan approksimoimaan.

Funktionaalin elektroni–elektroni-osa voidaan joka tapauksessa jakaa kahteen selvään komponenttiin: varaustiheyksien väliseen coulombiseen vuorovaikutukseen sekä ei-klassiseen osaan, joka sisältää elektronien vaihto- ja coulomb-korrelaation sekä varaustiheyden itseisvuorovaikutuksen:

$F_{HK}[\rho ]=T[\rho ]+E_{ee}[\rho ]=T[\rho ]+{\frac {1}{2}}\int \int {\frac {\rho ({\vec {r}}_{1})\rho ({\vec {r}}_{2})}{|{\vec {r}}_{1}-{\vec {r}}_{2}|}}d{\vec {r}}_{1}d{\vec {r}}_{2}+E_{ncl}[\rho ]=T[\rho ]+J[\rho ]+E_{ncl}[\rho ]$

Ainoa suure, joka siis voidaan suoraan laskea elektronitiheydestä on kahden varaustiheyden välinen repulsio. Ei-klassiselle vaihto- ja korrelaatio-osalle ja kineettiselle osalle ei tunneta funktionaaleja. Kohn ja Sham esittivät , että kineettistä energiaa voitaisiin approksimoida laskemalla se aivan kuten Hartree–Fock-menetelmässä eli kineettisen energian operaattorin odotusarvona, $\left\langle \Psi |{\hat {T}}|\Psi \right\rangle =\left\langle \Psi |-{\frac {1}{2}}\nabla ^{2}|\Psi \right\rangle$. Tätä varten täytyy luoda ei-vuorovaikuttava referenssisysteemi, joka koostuu yksielektroniorbitaaleista eli niin kutsutuista Kohn–Sham-orbitaaleista $\phi ^{KS}$. Hartree–Fock menetelmän tapaan referenssisysteemiä kuvaa yksi Slaterin determinantti ja jokaiselle orbitaalille kirjoitetaan Fock-operaattorin kaltainen Kohn–Sham-operaattori:

${\hat {f}}^{KS}=-{\frac {1}{2}}\nabla ^{2}+V_{S}({\vec {r}})$

Referenssisysteemin orbitaalien neliön tulee vastata oikean systeemin elektronitiheyttä, eli $\sum _{i}^{N}|\phi _{i}^{KS}|^{2}=\rho ({\vec {r}})$. Operaattorin potentiaalitermi $V_{S}({\vec {r}})$ muodostaa yhteyden oikean sekä referenssisysteemin välille ja on muotoa

$V_{S}({\vec {r}})=\int {\frac {\rho ({\vec {r}}_{2})}{|{\vec {r}}_{1}-{\vec {r}}_{2}|}}d{\vec {r}}_{2}-\sum _{k}{\frac {Z_{k}}{|{\vec {r}}_{1}-{\vec {R}}_{k}|}}+V_{XC}({\vec {r}}_{1})$

Ensimmäinen termi kuvaa orbitaalin vuorovaikutusta muiden orbitaalien kanssa, toinen termi kuvaa atomiydinten muodostamaa ulkoista potentiaalia ja $V_{XC}$ on niin kutsuttu vaihto- ja korrelaatiopotentiaali. Koska jokaisen orbitaalin Kohn–Sham-operaattori riippuu muista orbitaaleista, täytyy ominaisarvotehtävä ratkaista iteratiivisesti itseytyvän kentän (self-consistent field, SCF) avulla. Potentiaalitermi $V_{XC}$ saadaan vaihto- ja korrelaatioenergian funktionaaliderivaatasta:

$V_{XC}={\frac {\delta E_{XC}}{\delta \rho }}$

missä $E_{XC}[\rho ]=T_{C}[\rho ]+E_{ncl}[\rho ]$. Toisin sanoen vaihto- ja korrelaatioenergia sisältää uupuvan osan kineettisestä energiasta $T_{C}[\rho ]$, kun kineettistä energiaa approksimoidaan Kohn–Sham-orbitaaleilla sekä elektronien vuorovaikutusten ei-klassiset osat $E_{ncl}[\rho ]$. Tätä uupuvaa osaa kokonaisenergiafunktionaalista joudutaan approksimoimaan ja saatavat tulokset ovat hyvin riippuvaisia käytetystä funktionaalista, joten funktionaalin valinta on tehtävä huolella ja oltava perusteltavissa. Vaikka oikealle funktionaalille ei ole löydetty lauseketta, on sille johdettavissa ominaisuuksia joita vasten kehitettyjä funktionaaleja voidaan testata. Osa kehitetyistä funktionaaleista pohjautuu ainoastaan teoreettisiin argumentteihin (esimerkiksi Perdew–Burke–Ernzerhofin funktionaali PBE), toiset ovat parametrisoituja esimerkiksi kokeellisiin tuloksiin tai tarkkoihin kvanttimekaanisiin laskuihin.

Tiheysfunktionaaliteorian ongelmakohtia

Systeemin kokonaisenergia elektronien lukumäärän funktiona. Keltaisella piirretty kuvaaja kuvaa eksaktia energiaa ja vihreällä approksimatiivista funktionaalia. Approksimatiivisella funktionaalilla funktio ei ole lineaarinen kokonaislukuelektronien välillä ja konveksin profiilin vuoksi kokonaisenergia voi olla alhaisempi murto-osa elektroneilla.

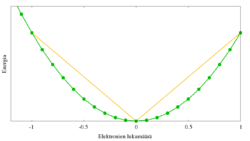
Huolimatta suuresta suosiostaan laskennallisten fyysikkojen ja kemistien keskuudessa, tiheysfunktionaaliteoriassa esiintyy silti lukuisia perustavanlaatuisia ongelmakohtia, jotka tuovat systemaattista virhettä tuloksiin. Virheet eivät sisälly varsinaiseen teoriaan vaan ovat seurausta vaihto- ja korrelaatiofunktionaalin approksimatiivisesta käsittelystä, joka johtaa muun muassa elektronien ylidelokalisoitumiseen sekä staattisen korrelaation virheelliseen kuvaamiseen.

Approksimatiivisten funktionaalien korrelaatiovirheen vuoksi nykyisellä tiheysfunktionaaliteorialla ei voida luotettavasti kuvata degeneerisiä tai miltei degeneerisiä tiloja, kemiallisen sidoksen katkeamista tai systeemejä, joissa elektronikorrelaatio on erityisen voimakasta. Elektronien ylidelokalisoitumisella on vastaavasti lukuisia seurauksia: reaktioiden liian alhaiset aktivaatioenergiat sekä materiaalien vyövälin, ionisten yhdisteiden dissosiaatioenergian ja varauksensiirtoreaktioiden reaktioenergian arvioiminen väärin.

Oikean systeemin kokonaisenergia on elektronien lukumäärän suhteen jatkuva funktio, mutta funktion derivaatta on epäjatkuva kokonaislukumäärien kohdalla johtuen elektronien diskreetistä luonteesta. Kokonaisenergia "murto-osaelektroneilla" saadaan siis interpoloimalla kahden kokonaislukuarvon väliltä. Approksimativiisilla funktionaaleilla kokonaisenergiassa ei epäjatkuvuuskohtia esiinny vaan funktio on konveksi ja systeemin energia on tämän vuoksi oikeaa energiaa alhaisempi.

Luettavaa

• W. Koch, M. C. Holthausen: A chemist's guide to density functional theory. Wiley-Vch Weinheim, 2001. ISBN 978-3-527-30372-4.
• C. J. Cramer: Essentials of computational chemistry: theories and models. John Wiley & Sons, Ltd, 2004. ISBN 978-0-470-09182-1.
• D. Cook: Handbook of computational quantum chemistry. Dover publications, Inc, 2005. ISBN 0-486-44307-8.