Kolmannen asteen käyrä

Kokoelma kolmannen asteen käyristä. Vertaa kuvaa tekstiin.

Kolmannen asteen käyrä on algebrallinen käyrä, jonka määrittelee yhtälö

F(x,y,z) = 0

sovellettuna homogeeniseen koordinaatistoon projektiivitasolle tai epähomogeeniseen avaruuteen, joka on määritelty asettamalla z = 1 em. yhtälössä. Tässä F on lineaarinen kombinaatio kolmannen asteen monomista

x³, y³, z³, x²y, x²z, y²x, y²z, z²x, z²y, xyz.

Kolmannen asteen käyrä on tasokäyrä, joka on muotoa

$a_{1}x^{3}+a_{2}x^{2}y+a_{3}xy^{2}+a_{4}y^{3}+a_{5}x^{2}+a_{6}xy+a_{7}y^{2}+a_{8}x+a_{9}y+a_{10}=0$

polynomin kuvaaja. Tutuin esimerkki tällaisesta käyrästä on kuutioparaabeli: y = b₁x³ + b₂x² + b₃x + b₄ = 0.

Kolmannen asteen käyrät voivat olla muodoltaan hyvin vaihtelevia. Yhteisenä piirteenä niille on kuitenkin, että ne voivat leikata suoran enintään kolmessa pisteessä.

Esimerkkejä

Alla olevissa kuvissa on joitakin esimerkkejä kolmannen asteen käyristä ja niiden yhtälöt.

• 

  Kuutioparaabeli
  $y=x^{3}$

• 

  Kolmannen asteen polynomifunktion kuvaaja
  y = ax³+bx²+cx+d

• 

  Descartesin lehti
  $x^{3}+y^{3}-3axy=0$

• 

  Diokleen kissoidi
  $(x^{2}+y^{2})x=2ay^{2}$

• 

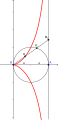
  de Sluzen konkoidi
  (x-1)(x²+y²) = ax²

• 

  Singulaarinen kolmannen asteen käyrä
  $y^{2}=x^{2}(x+1)$

• 

  Oikea strofoidi
  $y^{2}=x^{2}{\frac {a-x}{a+x}}$

• 

  Puolikuutioparaabeli
  $y^{2}=x^{3}$

• 

  Serpentiinikäyrä
  $y={\frac {abx}{x^{2}+a^{2}}}$

• 

  Tridenttikäyrä
  xy+ax³+bx²+cx = d

• 

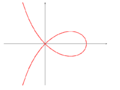
  Maclaurinin trisectrix
  2x(x²+y²) = a(3x²-y²)

• 

  Tschirnhausenin kuutiollinen käyrä
  $3ay^{2}=x(x-a)^{2}$

• 

  Agnesin noita
  $y={\frac {8a^{3}}{x^{2}+4a^{2}}}$

Lähteet

• A Catalog of Cubic Plane Curves (Arkistoitu – Internet Archive)